Содержание
- 2. Выпуклые многоугольники Пусть стороны выпуклого многоугольника лежат на прямых, задаваемых уравнениями которая и определяет этот многоугольник.
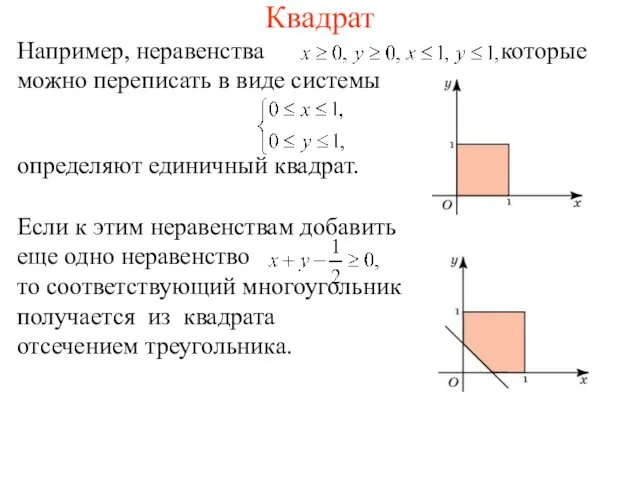
- 3. Квадрат Например, неравенства которые можно переписать в виде системы определяют единичный квадрат. Если к этим неравенствам
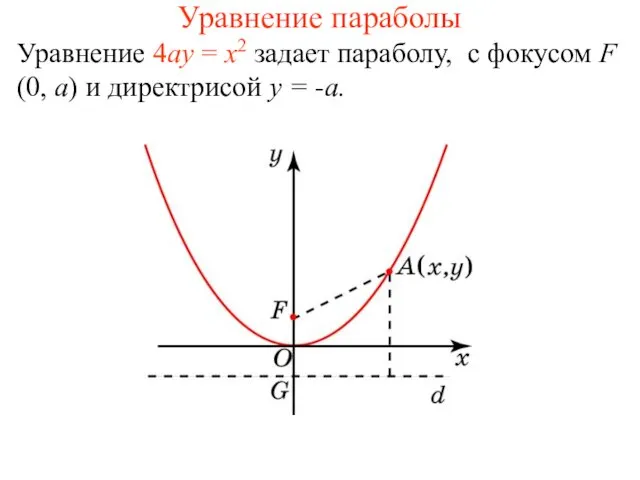
- 4. Уравнение параболы Уравнение 4ay = x2 задает параболу, с фокусом F (0, a) и директрисой y
- 5. Уравнение эллипса Уравнение (a > b) задает эллипс, с фокусами F1(-c, 0), F2(c, 0), где .
- 6. Уравнение гиперболы Уравнение (a > b) задает гиперболу, с фокусами F1(-c, 0), F2(c, 0), где .
- 7. Пример 1 Найдите неравенства, задающие треугольник с вершинами A(1, 0), B(0, 1), C(1, 1).
- 8. Пример 2 Для параболы, заданной уравнением y = x2, найдите координаты фокуса и уравнение директрисы.
- 9. Упражнение 1 Ответ: а) Первой; Определите, какой полуплоскости 5x + 3y - 2 0 или 5x
- 10. Упражнение 2 Какую фигуру задает следующая система неравенств Ответ: Прямоугольник.
- 11. Упражнение 3 Найдите фокус и директрису параболы, заданной уравнением y2 = x.
- 12. Упражнение 4 В каком случае уравнение эллипса дает окружность? Ответ: a = b.
- 13. Упражнение 5 Ответ: F1(0, 1), F2(0, -1). Для эллипса, заданного уравнением x2 + y2 = 1,
- 14. Упражнение 6 Для гиперболы, заданной уравнением x2 - y2 = 1, найдите координаты фокусов.
- 15. Упражнение 7 Решение: На координатной плоскости в качестве двух данных точек возьмем точки A(0, 0) и
- 16. Упражнение 8 Решение: На координатной плоскости в качестве точки F возьмем точку F(3, 0), а в
- 17. Упражнение 9 Расстояние от данной точки F до данной прямой d равно 3. Какой фигурой является
- 18. Упражнение 10 Лемниската Бернулли представляет собой геометрическое место точек, произведение расстояний от которых до двух фиксированных
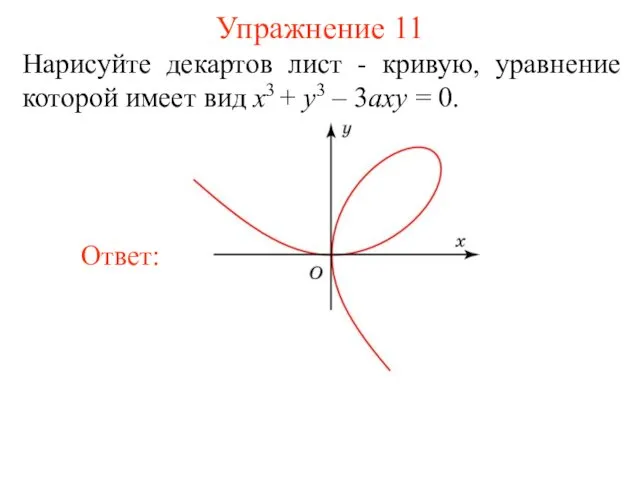
- 19. Упражнение 11 Нарисуйте декартов лист - кривую, уравнение которой имеет вид x3 + y3 – 3axy
- 20. Параметрические уравнения Рассмотрим вопрос о том как траектория движения точки описывается с помощью уравнений. Поскольку положение
- 21. Окружность Окружность. Окружность радиуса R с центром в начале координат можно рассматривать как параметрически заданную кривую
- 22. Циклоида Найдем параметрические уравнения циклоиды. Предположим, что окружность повернулась на некоторый угол величины t. При этом
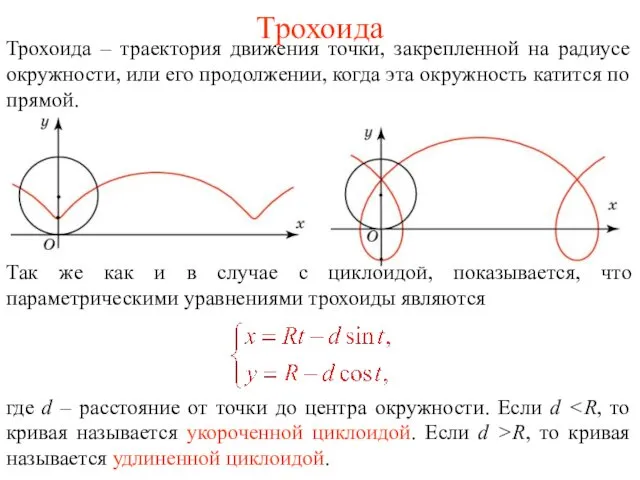
- 23. Трохоида Трохоида – траектория движения точки, закрепленной на радиусе окружности, или его продолжении, когда эта окружность
- 24. Эпициклоиды Пусть центр O неподвижной окружности является началом координат и точка A(R, 0) соответствует начальному моменту
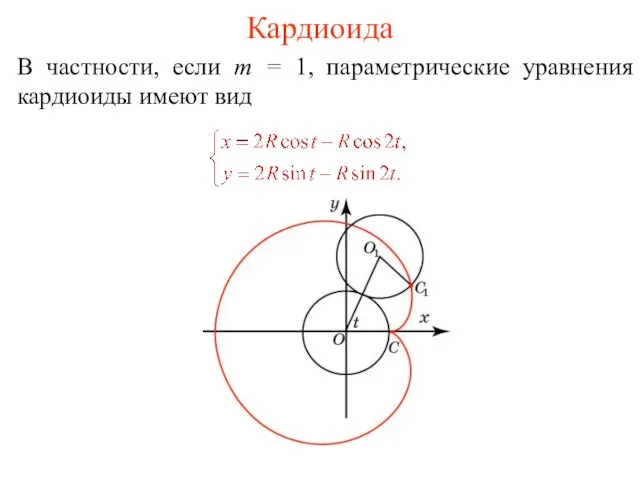
- 25. Кардиоида В частности, если m = 1, параметрические уравнения кардиоиды имеют вид
- 26. Эпициклоида (m = 2/3) Параметрические уравнения эпициклоиды имеют вид
- 27. Удлиненная эпициклоида (m = 2/3) Параметрические уравнения удлиненной эпициклоиды имеют вид
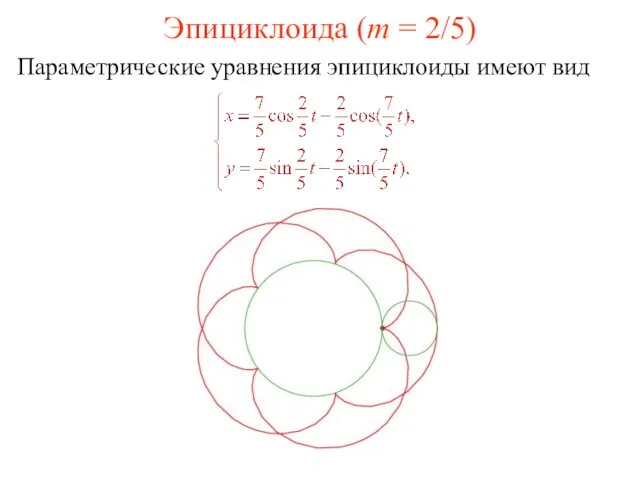
- 28. Эпициклоида (m = 2/5) Параметрические уравнения эпициклоиды имеют вид
- 29. Гипоциклоиды Так же как и для эпициклоиды показывается, что уравнения гипоциклоиды имеют вид
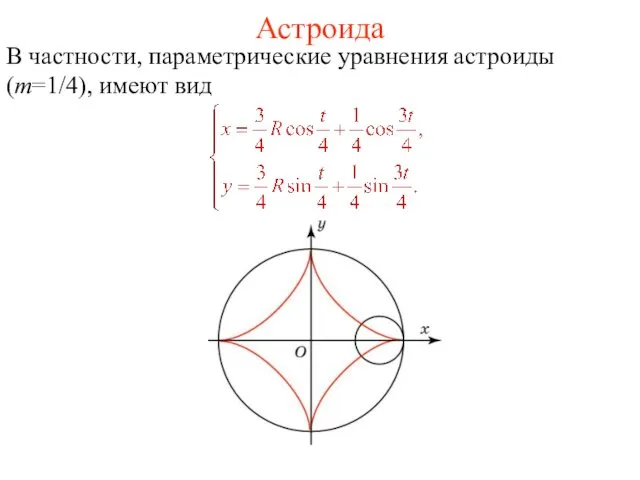
- 30. Астроида В частности, параметрические уравнения астроиды (m=1/4), имеют вид
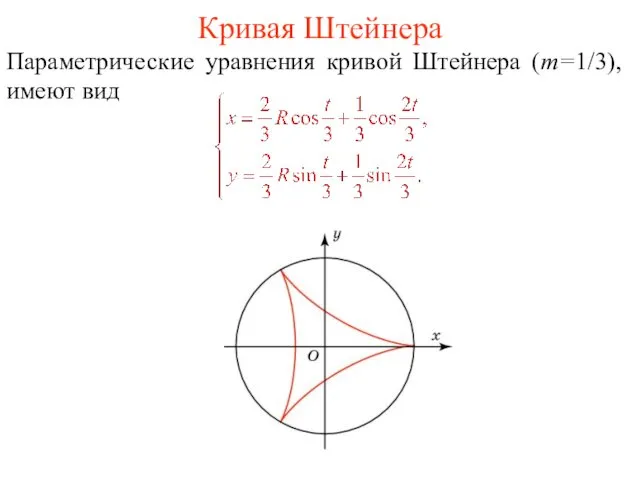
- 31. Кривая Штейнера Параметрические уравнения кривой Штейнера (m=1/3), имеют вид
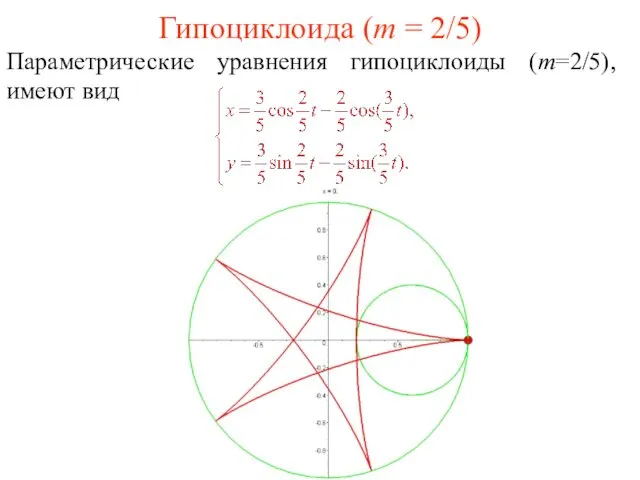
- 32. Гипоциклоида (m = 2/5) Параметрические уравнения гипоциклоиды (m=2/5), имеют вид
- 33. Упражнение 12 Найдите параметрические уравнения окружности с центром в точке O(x0, y0) и радиусом R.
- 34. Упражнение 12 Найдите параметрические уравнения прямой, проходящей через точки A1(x1, y1) и A2(x2, y2).
- 35. Упражнение 14 Какую кривую задают параметрические уравнения ? Ответ. Парабола.
- 37. Скачать презентацию

























 Великолепная пятерка. Игра
Великолепная пятерка. Игра Білімді тиянақтау
Білімді тиянақтау Мастер-класс по внеурочной деятельности по рабочей программе «Занимательная геометрия»
Мастер-класс по внеурочной деятельности по рабочей программе «Занимательная геометрия» Магия чисел. Мастерское число
Магия чисел. Мастерское число Свойства корня п- ой степени
Свойства корня п- ой степени Презентация на тему Числовой отрезок
Презентация на тему Числовой отрезок Каков развивающий потенциал функциональной линии в курсе математики?
Каков развивающий потенциал функциональной линии в курсе математики? Решение задач с использованием формулы полной вероятности и формулы Бейеса
Решение задач с использованием формулы полной вероятности и формулы Бейеса Вычислительная механика. Конечные элементы с нелинейной аппроксимацией
Вычислительная механика. Конечные элементы с нелинейной аппроксимацией Презентация по математике "Системы исчисления" - скачать бесплатно
Презентация по математике "Системы исчисления" - скачать бесплатно Круговые диаграммы
Круговые диаграммы Арккосинус а. Решение уравнений
Арккосинус а. Решение уравнений Закономерности между элементами фигуры и тенью при освещении параллельными лучами
Закономерности между элементами фигуры и тенью при освещении параллельными лучами Свойства арифметического корня п–ой степени
Свойства арифметического корня п–ой степени Подготовка к ЕГЭ. Об особенностях решения заданий С2 ЕГЭ
Подготовка к ЕГЭ. Об особенностях решения заданий С2 ЕГЭ Муниципальное общеобразовательное учреждение гимназия № 70 г. Екатеринбурга Информационно исследовательский проект Лавровой А
Муниципальное общеобразовательное учреждение гимназия № 70 г. Екатеринбурга Информационно исследовательский проект Лавровой А Конус. Объём усечённого конуса
Конус. Объём усечённого конуса Гексаэдр
Гексаэдр Презентация по математике "Прямоугольная система координат на плоскости" - скачать бесплатно
Презентация по математике "Прямоугольная система координат на плоскости" - скачать бесплатно Предикаты и кванторы. Действия над предикатами и их свойства
Предикаты и кванторы. Действия над предикатами и их свойства Прямоугольник. Ось симметрии фигуры
Прямоугольник. Ось симметрии фигуры Свойства действий над числами
Свойства действий над числами Координатная плоскость
Координатная плоскость Презентация по математике "Занимательные математические задачи. Математические ребусы" - скачать
Презентация по математике "Занимательные математические задачи. Математические ребусы" - скачать  Прямоугольный параллелепипед
Прямоугольный параллелепипед Цифра 10
Цифра 10 Координаты вектора
Координаты вектора Урок алгебры в 7 классе. Учитель МОУ СОШ №21 Мариничева И.М.
Урок алгебры в 7 классе. Учитель МОУ СОШ №21 Мариничева И.М.