Содержание
- 2. задачи на нахождение площади фигур, изображённых на клетчатой бумаге, можно решить с помощью формулы Пика более
- 3. Методы исследования: сравнение, обобщение. Задачи: Изучить литературу по данной теме. Прорешать задачи на нахождение площади фигур,
- 4. Актуальность: тема решения геометрических задач по формуле Пика является актуальной, т. к. ее изучение может быть
- 5. Триангуляция многоугольника. Любой п - угольник можно разрезать диагоналями на треугольники, причём количество треугольников будет равно
- 6. Экспериментальная работа. Нахождение площади многоугольника геометрическим методом Задача1. Найдите площадь треугольника ABC, считая стороны квадратных клеток
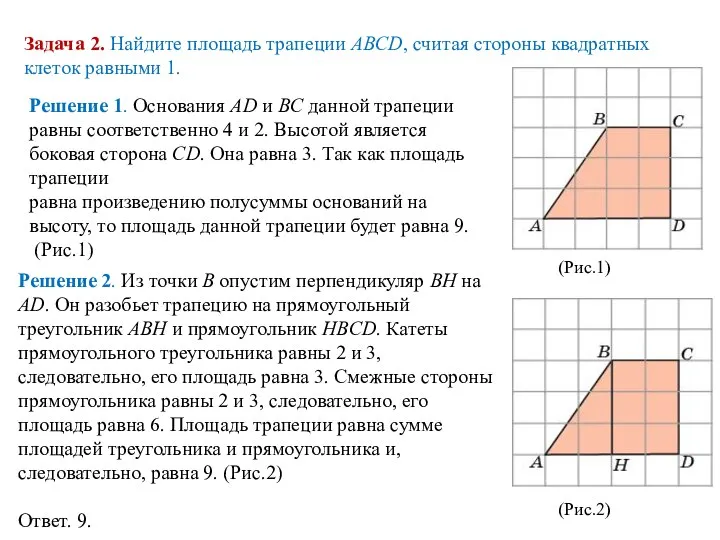
- 7. Задача 2. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1. Решение 1. Основания AD
- 8. Задача 3..Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите S/π. Решение
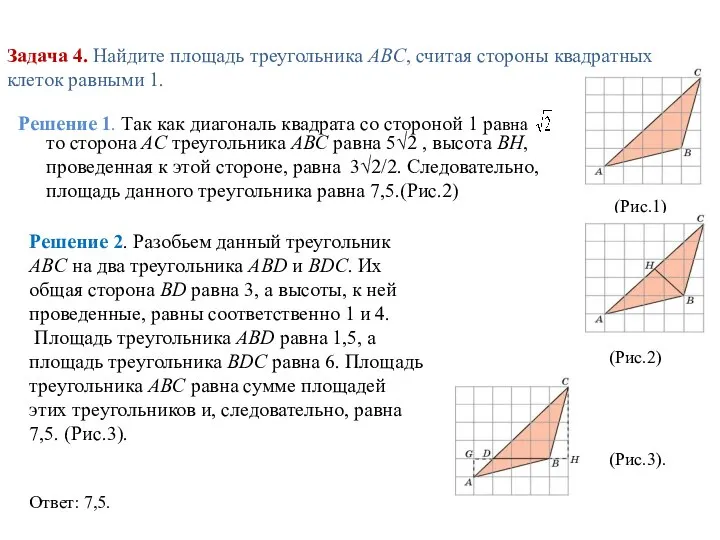
- 9. Задача 4. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1. (Рис.1) Решение 1. Так
- 10. Задача 5. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1. Рис.1 Рис.2 Решение 1.
- 11. Задача 6. Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите .
- 12. Нахождение площади многоугольника по формуле Пика. Задача 1. Найдите площадь треугольника ABC, считая стороны квадратных клеток
- 13. Задача 3. Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите .
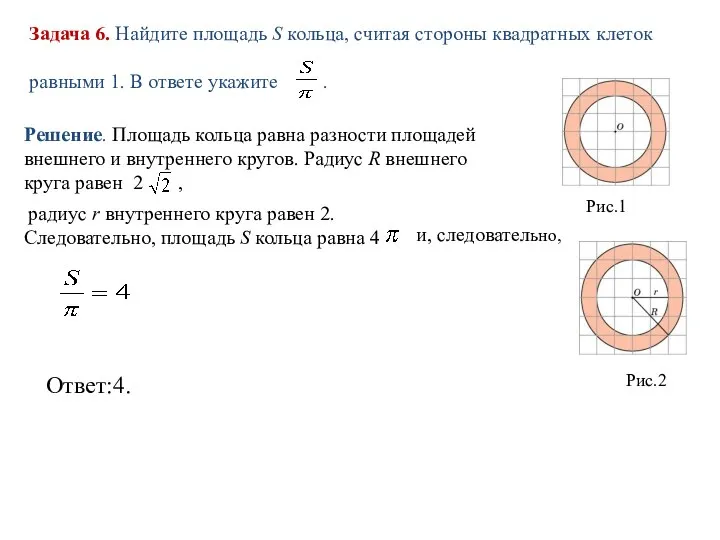
- 14. Задача 6. Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите .
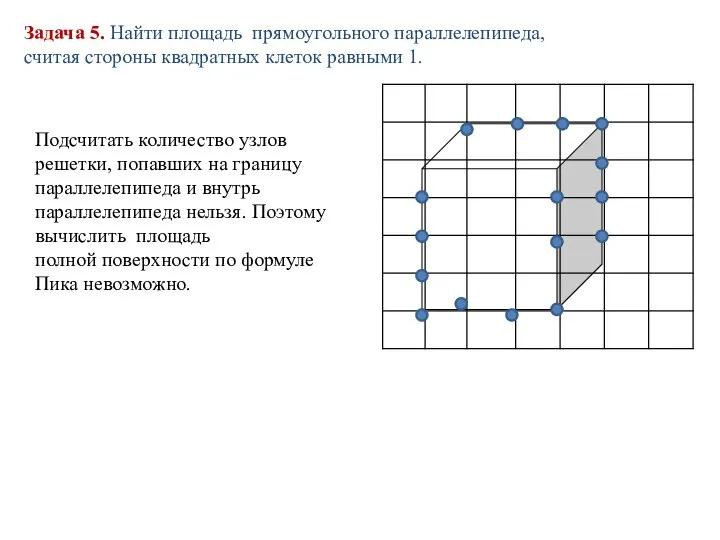
- 15. Задача 5. Найти площадь прямоугольного параллелепипеда, считая стороны квадратных клеток равными 1. Подсчитать количество узлов решетки,
- 17. Скачать презентацию










 КАК ЛЮДИ СЧИТАЛИ В СТАРИНУ И КАК ПИСАЛИ ЦИФРЫ Демонстрационный материал к уроку
КАК ЛЮДИ СЧИТАЛИ В СТАРИНУ И КАК ПИСАЛИ ЦИФРЫ Демонстрационный материал к уроку  Степень с рациональным показателем. Степенная функция
Степень с рациональным показателем. Степенная функция Цилиндр. Конус
Цилиндр. Конус Что такое математика?
Что такое математика? Неравенства. Методика систематизации знаний при подготовке к ГИА
Неравенства. Методика систематизации знаний при подготовке к ГИА Первообразные
Первообразные Задачи по аналитической геометрии на плоскости. Уравнения прямой на плоскости
Задачи по аналитической геометрии на плоскости. Уравнения прямой на плоскости Цель диагностики математического развития детей
Цель диагностики математического развития детей Свойства действий с рациональными числами. Часть 2
Свойства действий с рациональными числами. Часть 2 Предварительный эксперимент и методы его анализа
Предварительный эксперимент и методы его анализа Презентация на тему Скорость сближения и удаления
Презентация на тему Скорость сближения и удаления  Разбор задач
Разбор задач Действия над комплексными числами в алгебраической форме
Действия над комплексными числами в алгебраической форме Математика 1 класс
Математика 1 класс  Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний
Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний Повтарение по математике. Уравнение
Повтарение по математике. Уравнение Презентация по математике "Математика – гимнастика ума" - скачать бесплатно
Презентация по математике "Математика – гимнастика ума" - скачать бесплатно Реляционная алгебра. Операторы
Реляционная алгебра. Операторы Связь математики с биологией
Связь математики с биологией Комбинаторика. 5 класс
Комбинаторика. 5 класс Аттестационная работа. Методическая разработка по выполнению проекта Геометрия на клетчатой решетке
Аттестационная работа. Методическая разработка по выполнению проекта Геометрия на клетчатой решетке Параллельные алгоритмы вычислительной алгебры. Разделение переменных
Параллельные алгоритмы вычислительной алгебры. Разделение переменных Математика в педиатрии Выполнила:
Математика в педиатрии Выполнила:  Формула площади прямоугольника. Математика повсюду, Глазом только поведёшь – И примеров разных уйму, Где применить её найдё
Формула площади прямоугольника. Математика повсюду, Глазом только поведёшь – И примеров разных уйму, Где применить её найдё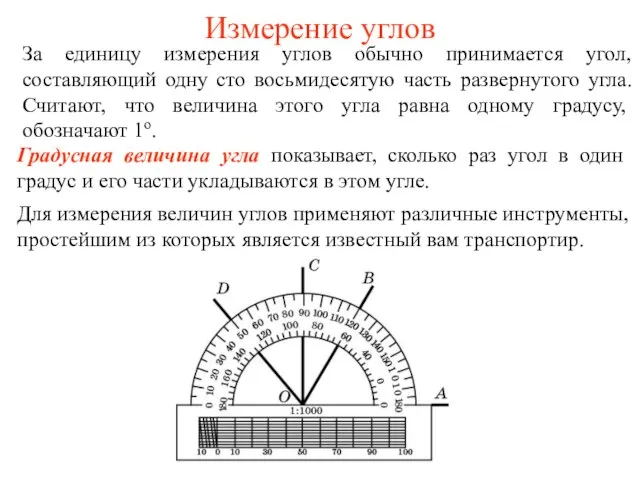 Измерение углов. Вопросы, упражнения
Измерение углов. Вопросы, упражнения Презентация по математике "Логические задачи 1 класс" - скачать бесплатно
Презентация по математике "Логические задачи 1 класс" - скачать бесплатно Тригонометрические уравнения
Тригонометрические уравнения Линейная алгебра. Невырожденные матрицы. Обратная матрица. Матричные уравнения
Линейная алгебра. Невырожденные матрицы. Обратная матрица. Матричные уравнения