- Главная
- Математика
- Булева алгебра

Содержание
- 2. План: Булева алгебра и логические схемы ЭВМ Этапы построения логической схемы Алгоритм составления СДНФ Основные законы
- 3. Булева алгебра и логические схемы ЭВМ Алгебра логики, созданная в середине 18 века англичанином Дж. Булем
- 4. Таблица истинности
- 5. Этапы построения логической схемы: Алгоритм составления СДНФ: составляется таблица истинности; по таблице истинности строится логическая функция
- 6. Основные законы булевой алгебры Таблица 2 1. {0 1}`={1 0}; x+0=x*1=x; x+1=1; x*0=0 -//-//-//-//-//- 2. x+x=x;
- 7. Логические основы ЭВМ. Элемент И (AND). Электронный логический элемент, на выходе которого появляется сигнал логической 1,
- 8. Элемент ИЛИ (OR gate). Электронный логический вентиль, на выходе которого логический 0 (значение "ложь") появляется только
- 9. Алгебра Дж. Буля и ее применение в теории и практике информатики Информация, с которой имеют дело
- 10. Поскольку любая алфавитная (буквенно-цифровая) информация может быть закодирована в двоичной форме, то подобным образом могут быть
- 11. /\ V z = x /\ y z = x V y z = x х
- 13. Процессоры Процессором называется устройство, способное выполнять некоторый заданный набор операций над данными в структурированной памяти и
- 14. Заключение Булеву алгебру образуют все подмножества некоторого множества. То, что они образуют решетчатую структуру, очевидно. Нетрудно
- 16. Скачать презентацию
План:
Булева алгебра и логические схемы ЭВМ
Этапы построения логической схемы
Алгоритм
План:
Булева алгебра и логические схемы ЭВМ
Этапы построения логической схемы
Алгоритм
Основные законы булевой алгебры
Логические основы ЭВМ.
Алгебра Дж. Буля и ее применение в теории и практике информатики
Процессоры
Заключение
Булева алгебра и логические схемы ЭВМ
Алгебра логики, созданная в середине
Булева алгебра и логические схемы ЭВМ
Алгебра логики, созданная в середине
В электронных схемах операции выполняются с помощью логических элементов. При этом логические сигналы 0 и 1 задаются разными уровнями напряжения. Для изображения логических схем всегда используются условные графические обозначения элементов, описывающие только выполняемую элементами функцию и не зависящие от его схемы.
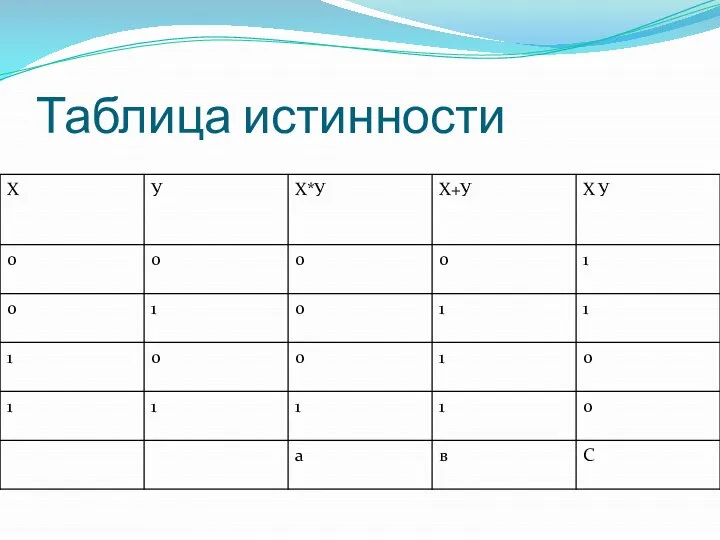
Таблица истинности
Таблица истинности
Этапы построения логической схемы:
Алгоритм составления СДНФ:
составляется таблица истинности;
по
Этапы построения логической схемы:
Алгоритм составления СДНФ:
составляется таблица истинности;
по
по возможности полученная формула минимизируется;
если заданы базисные элементы, то с помощью законов Моргана приводится к заданному базису.
выделяем в таблице истинные строки, в которых функция принимает единственные значения;
для каждой выделенной строки составляются конъюнкции всех входных переменных; если переменные принимают нулевое значение, сделать их отрицание;
записывается попарная дизъюнкция всех полученных конъюнкций.
Основные соотношения (теоремы) булевой алгебры можно сформулировать в виде следующих законов (табл. 2):
Основные законы булевой алгебры
Таблица 2
1. {0 1}`={1 0}; x+0=x*1=x;
Основные законы булевой алгебры
Таблица 2
1. {0 1}`={1 0}; x+0=x*1=x;
2. x+x=x; x*x=x Идемпотентности
3. (x`)`=x Двойного отрицания
4. x+y=y+x; x*y=y*x Коммутативности
5. x+x*y=x*(x+y)=x; x+x`* y=x+y; x*(x`+y)=x*y Поглощения
6. (x+y)`-x`*y`; (x*y)`=x`+y` Моргана
7. (x+y)+z=x+(y+z)=x+y+z; (x*y)* z=x*(y*z)=x*y*z Ассоциативности
8. x+y*z=(x+y)*(x+z); x* (y+z)=x*y+x*z Дистрибутивности
Логические основы ЭВМ.
Элемент И (AND).
Электронный логический элемент, на выходе
Логические основы ЭВМ.
Элемент И (AND).
Электронный логический элемент, на выходе
Условное обозначение и таблица истинности элемента "И" с двумя выходами.
Элемент ИЛИ (OR gate).
Электронный логический вентиль, на выходе которого
Элемент ИЛИ (OR gate).
Электронный логический вентиль, на выходе которого
А2 0 1 0 1
Выход В 0 1 1 1
Элемент НЕ-И (штрих Шеффера).
Электронная логическая схема, в которой выходной сигнал имеет уровень логической 0 (ложь) только тогда, когда на всех ее входах действуют сигналы логической 1. Во всех других случаях на его выходе появляется логическая 1.
А2 0 1 0 1
Выход В 1 1 1 0
Вентиль НЕ-И эквивалентен И с инвертированным выходом.
Элемент ИЛИ-НЕ(стрелка Пирса).
Электронная логическая схема, на выходе у которой появляется логическая 1 только тогда, когда на все ее входы поданы сигналы логического 0, а в любых других случаях на выходе схемы действует уровень логического 0.
А2 0 1 0 1
Выход В 1 0 0 0
Практически любые схемы могут быть построены на одних только элементах ИЛИ-НЕ.
Элемент НЕ (NOT gate).
Электронный логический вентиль, инвертирующий входной сигнал, т.е. преобразующий логический 0 в логическую 1 и наоборот.
Выход В И Л
Алгебра Дж. Буля и ее применение в теории и практике информатики
Информация,
Алгебра Дж. Буля и ее применение в теории и практике информатики
Информация,
Данные разбиваются на отдельные составляющие, называемые элементарными данными или элементами данных. Употребляются элементы данных различных типов. Тип данных (элементарных) зависит от значений, которые эти данные могут принимать.
В современной безбумажной информатике среди различных типов элементарных данных наиболее употребительными являются целые и вещественные числа, слова (в некотором подалфавите байтового алфавита) и так называемые булевы величины. Первые два типа величин нуждаются в пояснении только в связи с конкретными особенностями их представления в современных ЭВМ.
Прежде всего различают двоичное и двоично-десятичное представления чисел. В двоичном представлении используется двоичная система счисления с фиксированным числом двоичных разрядов (чаще всего 32 или, для малых ЭВМ, 16 разрядов, включая разряд для представления знака числа). Если нулем обозначать плюс, а единицей — минус, то 00001010 означает целое число +(23+2l)= + l0, а 10001100— число— (23 + 22) = —12 (для простоты взято 8-разрядное представление). Заметим, что знак числа в машинном представлении часто оказывается удобным ставить не в начале, а в конце числа.
Поскольку любая алфавитная (буквенно-цифровая) информация может быть закодирована в двоичной форме,
Поскольку любая алфавитная (буквенно-цифровая) информация может быть закодирована в двоичной форме,
Существуют различные способы представления булевых величин (двоичных цифр) в виде тех или иных физических (обычно электрических) сигналов (высокое и низкое напряжение, импульсы тока разной полярности и т. п.).
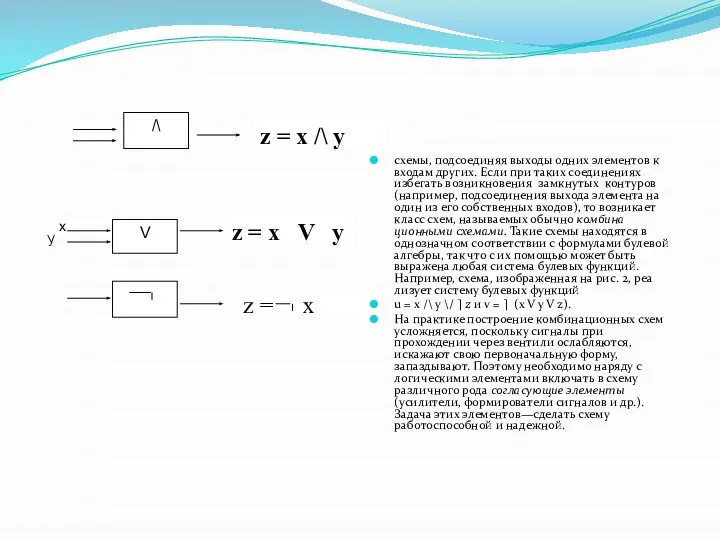
Выбрав форму представления (двоичных) сигналов, можно построить элементарные устройства, называемые обычно логическими вентилями (или логическими элементами), которые реализуют элементарные булевы операции. Иными словами, выходные
сигналы этих устройств представляют собой элементарные булевы функции (результат выполнения элементарных булевых операций) от входных сигналов, как это показано на рис. 1.
/\
V
z = x /\ y
z = x V y
z = x
/\
V
z = x /\ y
z = x V y
z = x
х
y
x
y
x
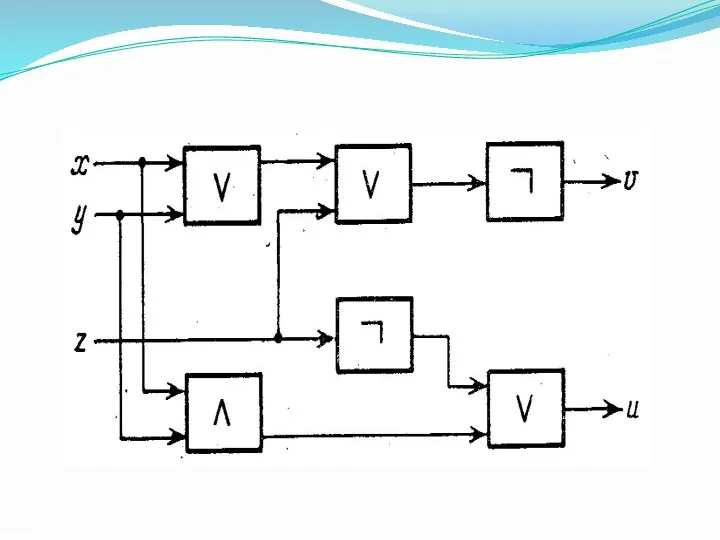
схемы, подсоединяя выходы одних элементов к входам других. Если при таких соединениях избегать возникновения замкнутых контуров (например, подсоединения выхода элемента на один из его собственных входов), то возникает класс схем, называемых обычно комбинационными схемами. Такие схемы находятся в однозначном соответствии с формулами булевой алгебры, так что с их помощью может быть выражена любая система булевых функций. Например, схема, изображенная на рис. 2, реализует систему булевых функций
u = x /\ y \/ ⎤ z и v = ⎤ (x V y V z).
На практике построение комбинационных схем усложняется, поскольку сигналы при прохождении через вентили ослабляются, искажают свою первоначальную форму, запаздывают. Поэтому необходимо наряду с логическими элементами включать в схему различного рода согласующие элементы (усилители, формирователи сигналов и др.). Задача этих элементов—сделать схему работоспособной и надежной.
Процессоры
Процессором называется устройство, способное выполнять некоторый заданный набор операций над данными
Процессоры
Процессором называется устройство, способное выполнять некоторый заданный набор операций над данными
Стандартная схема процессора состоит из двух устройств, называемых обычно арифметико-логическим устройством (АЛУ) и устройством управления (УУ). В схему АЛУ включается структурированная память, состоящая, как правило, из регистров, к которым может добавляться один или несколько стеков, С помощью специальных комбинационных схем в структурированной памяти может осуществляться тот или иной набор преобразований.
Как уже отмечалось выше, преобразования (операции), задаваемые комбинационными схемами, на сегодняшнем этапе развития микроэлектроники предпочитают делать достаточно простыми. Поэтому операции, выполняемые АЛУ за один такт синхронизирующего генератора, называются микрооперациями, а соответствующий их выполнению такт — микротактом. Выбор той или иной микрооперации осуществляется путем подачи кода этой микрооперации на специальный управляющий вход АЛУ.
Заключение
Булеву алгебру образуют все подмножества некоторого множества. То, что они
Заключение
Булеву алгебру образуют все подмножества некоторого множества. То, что они










 Математические модели и методы
Математические модели и методы Теорема о точке пересечения высот треугольника
Теорема о точке пересечения высот треугольника Модель конфликта
Модель конфликта ЛОГАРИФМ. Свойства логарифма.
ЛОГАРИФМ. Свойства логарифма. Прямоугольник. Ромб. Квадрат
Прямоугольник. Ромб. Квадрат Подготовка к контрольной работе
Подготовка к контрольной работе Решаем со Смешариками
Решаем со Смешариками Одночлены и многочлены
Одночлены и многочлены Комбинаторика
Комбинаторика Арифметическая прогрессия (9 класс)
Арифметическая прогрессия (9 класс) Соотношение между сторонами и углами прямоугольного треугольника (задачи по готовым чертежам)
Соотношение между сторонами и углами прямоугольного треугольника (задачи по готовым чертежам) Метод областей для решения систем неравенств с двумя переменными
Метод областей для решения систем неравенств с двумя переменными Решение задач на готовых чертежах 8 класс
Решение задач на готовых чертежах 8 класс Викторина. Первый тур
Викторина. Первый тур Последний герой
Последний герой Подготовка к ГИА по математике
Подготовка к ГИА по математике Первообразная функции. Неопределенный интеграл
Первообразная функции. Неопределенный интеграл Основы логики
Основы логики Решение уравнения cosx = a. Понятие арккосинуса числа
Решение уравнения cosx = a. Понятие арккосинуса числа Математическая шифровка
Математическая шифровка Математические станции
Математические станции Тема: Деление десятичных дробей на натуральные числа. Цель урока: закрепить навыки деления десятичной дроби на натуральное число
Тема: Деление десятичных дробей на натуральные числа. Цель урока: закрепить навыки деления десятичной дроби на натуральное число Движение в пространстве
Движение в пространстве Дробно-рациональные уравнения. Применение при решении задач
Дробно-рациональные уравнения. Применение при решении задач Векторы. Геометрия (9 класс)
Векторы. Геометрия (9 класс) Элективный курс. Алгебра 11 класс
Элективный курс. Алгебра 11 класс Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств Муниципальное казенное общеобразовательное учреждение Сайдыпская основная общеобразовательная школа. Устный счет на уроках ма
Муниципальное казенное общеобразовательное учреждение Сайдыпская основная общеобразовательная школа. Устный счет на уроках ма