Содержание
- 2. CONTEÚDO PROGRAMÁTICO DESTA AULA Equações diferenciais de 1a ordem - continuação Método de Runge- Kutta (Euler
- 3. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Uma Equação Diferencial Ordinária (EDO) é uma equação da forma F(x, y(x), y’(x),
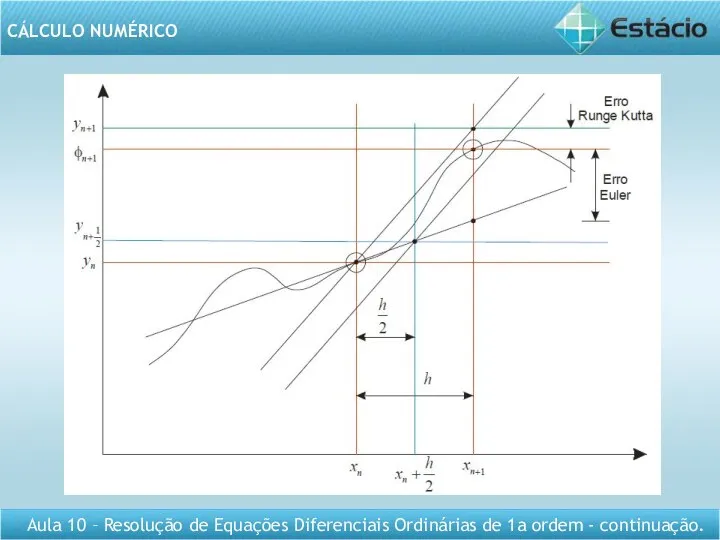
- 4. MÉTODO DE RUNGE-KUTTA O método de Runge-Kutta pode ser entendido como um aperfeiçoamento do método de
- 6. MÉTODO DE RUNGE-KUTTA O método de Euler é o método de Runge-Kutta de 1ª ordem; No
- 7. MÉTODO DE EULER É um método de passo 1, isto é, para determinar y n+1 precisamos
- 8. MÉTODO DE RUNGE-KUTTA DE ORDEM p É um método de passo 1, isto é, para determinar
- 9. MÉTODO DE RUNGE-KUTTA Como é um aperfeiçoamento do método de Euler devemos ter que y’ =
- 10. EXEMPLO 1 – Resolva o problema de valor inicial Usando o método de Euler modificado encontre
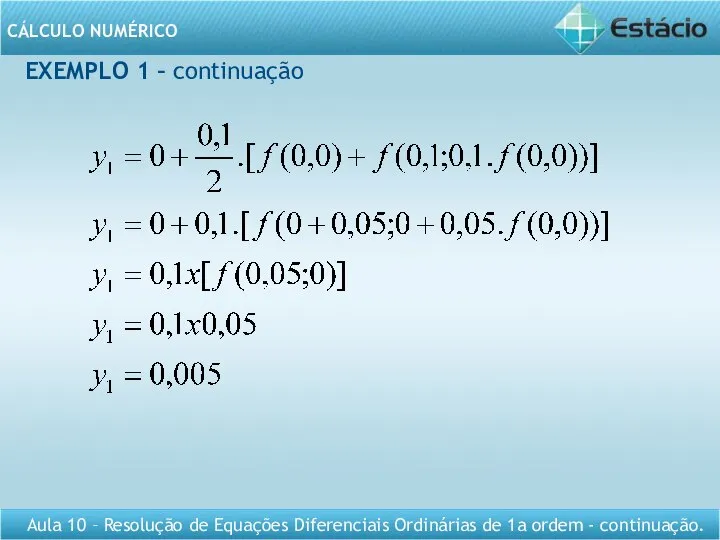
- 11. EXEMPLO 1 – continuação
- 12. EXEMPLO 1 – continuação X1 = 0 + 0,1 = 0,1 e y1=0,005
- 13. EXEMPLO 2 – Resolver o problema de valor inicial Determinar y(1) Euler X0 = 0 ;
- 14. EXEMPLO 2 – continuação b) Euler modificado X0 = 0 ; y0= 1.000 e h =
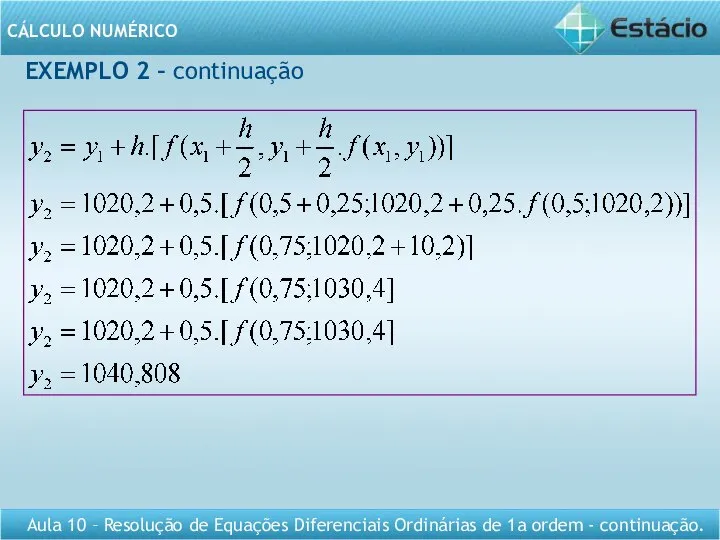
- 15. EXEMPLO 2 – continuação
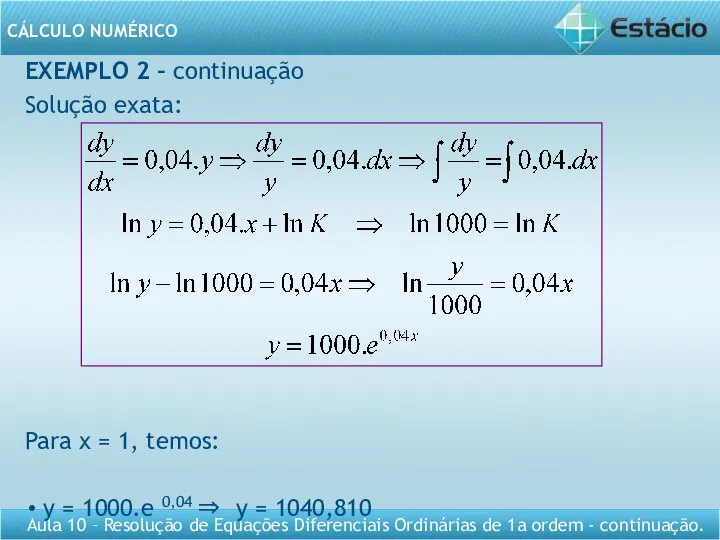
- 16. EXEMPLO 2 – continuação Solução exata: Para x = 1, temos: y = 1000.e 0,04 ⇒
- 18. Скачать презентацию











 Деление. Обобщение материала
Деление. Обобщение материала Школа Квентин – подготовка к ЕГЭ
Школа Квентин – подготовка к ЕГЭ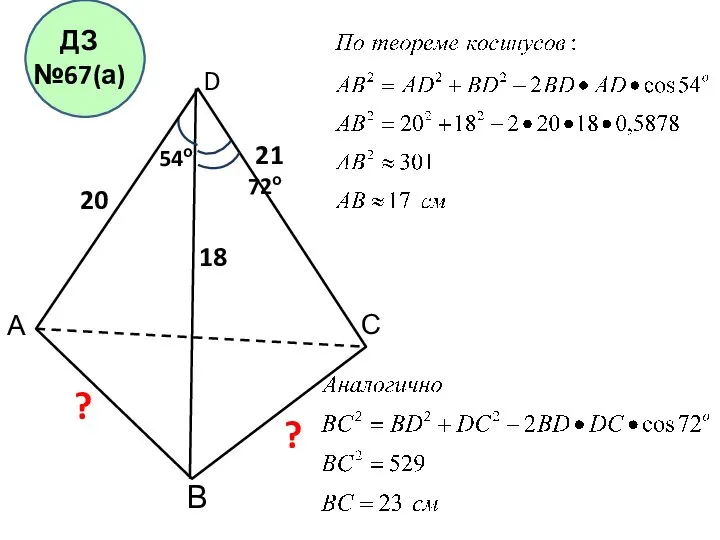 Параллелепипед. Урок 19
Параллелепипед. Урок 19 Применение теоремы Пифагора
Применение теоремы Пифагора Аттестационная работа. Проектная и исследовательская деятельность на уроках математики
Аттестационная работа. Проектная и исследовательская деятельность на уроках математики Умножение и деление натуральных чисел Математика 5 класс БИКЛАМБЕТОВА РАМЗИЯ АНВАРОВНА МКОУ «ОСЫПНОБУГОРСКАЯ СОШ»
Умножение и деление натуральных чисел Математика 5 класс БИКЛАМБЕТОВА РАМЗИЯ АНВАРОВНА МКОУ «ОСЫПНОБУГОРСКАЯ СОШ»  Интегралды
Интегралды Аксиомы стереометрии. 10 класс
Аксиомы стереометрии. 10 класс Shortest Paths
Shortest Paths Введение в геометрию. Точка и прямая
Введение в геометрию. Точка и прямая Два вида фиктивных переменных
Два вида фиктивных переменных Симметрия в архитектуре
Симметрия в архитектуре Алтын қақпа
Алтын қақпа Элементы теории алгоритмов
Элементы теории алгоритмов Математический диктант: флаги
Математический диктант: флаги Презентация по математике "Единицы меры площади" - скачать бесплатно
Презентация по математике "Единицы меры площади" - скачать бесплатно Сходимость последовательности СВ
Сходимость последовательности СВ Три М: математика, мнемоника, мотивация
Три М: математика, мнемоника, мотивация Правильные многоугольники
Правильные многоугольники Элементы комбинаторики, статистики и теории вероятностей. Решение заданий В 10 ЕГЭ
Элементы комбинаторики, статистики и теории вероятностей. Решение заданий В 10 ЕГЭ Гамильтоновы циклы
Гамильтоновы циклы Напівправильні многогранники
Напівправильні многогранники Тригонометрические уравнения 10 класс
Тригонометрические уравнения 10 класс Письмове додавання і віднімання чисел. Урок №126
Письмове додавання і віднімання чисел. Урок №126 Исследование функций и построение графиков
Исследование функций и построение графиков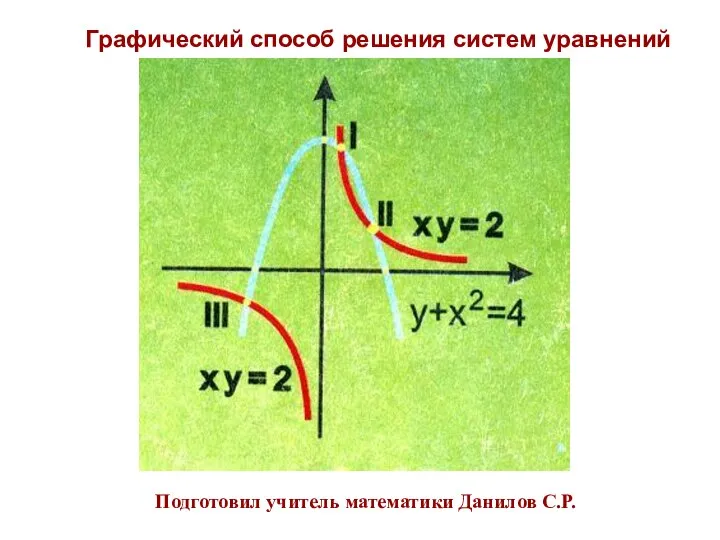 Графический способ решения систем уравнений
Графический способ решения систем уравнений Единицы измерения длины
Единицы измерения длины Площадь круга
Площадь круга