Содержание
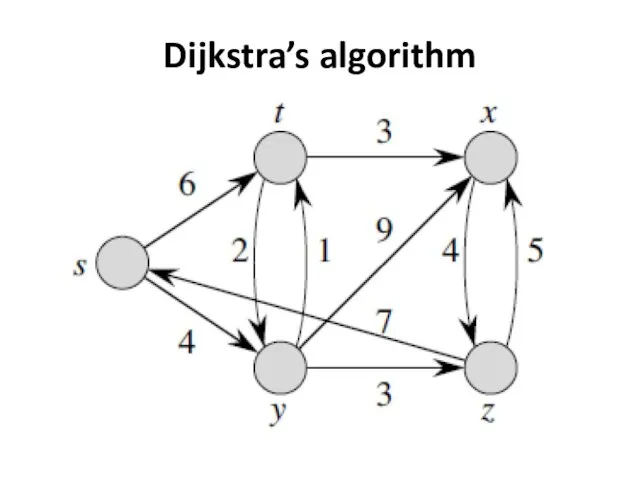
- 2. Dijkstra’s algorithm are given: source vertex s; the weight weight (u, v) of each edge (u,
- 3. Dijkstra’s algorithm
- 4. Dijkstra’s algorithm the situation at time 0 shortest[s]= 0
- 5. Dijkstra’s algorithm at time 4 shortest[y]= 4, pred[y]= s
- 6. Dijkstra’s algorithm at time 5 shortest[t]=5, pred[t]= y
- 7. Dijkstra’s algorithm at time 7 shortest[z]=7, pred[z]= y
- 8. Dijkstra’s algorithm at time 8 shortest[x]=8, pred[x]=t
- 9. Dijkstra’s algorithm Dijkstra’s algorithm works a little differently. It treats all edges the same. Dijkstra’s algorithm
- 11. Dijkstra’s algorithm A set Q is a set of vertices for which the final shortest and
- 12. Dijkstra’s algorithm A set Q is a set of vertices for which the final shortest and
- 13. Dijkstra’s algorithm Question 1: How does the algorithm find new paths and do the relaxation? Question
- 14. Dijkstra’s algorithm
- 15. Dijkstra’s algorithm Answer to Question 1: How does the algorithm find new paths and do the
- 16. Dijkstra’s algorithm Remaid: The Algorithm for Relaxing an Edge. Relax(u, v) { If (shortest[u] + weight(u,v)
- 17. Dijkstra’s algorithm Idea of Dijkstra’s Algorithm: Repeated Relaxation Dijkstra’s algorithm operates by maintaining a subset of
- 18. Dijkstra’s algorithm Idea of Dijkstra’s Algorithm: Repeated Relaxation Initially Q=NULL, the empty set, and we set
- 19. Dijkstra’s algorithm Idea of Dijkstra’s Algorithm: Repeated Relaxation The set Q can be implemented using an
- 20. Dijkstra’s algorithm The Selection in Dijkstra’s Algorithm Recall Question 2: What is the best order in
- 21. Dijkstra’s algorithm Question 2: How does the algorithm select which vertex among the vertices of V\Q?
- 22. Dijkstra’s algorithm Question: How do we implement this selection of vertices efficiently? Answer: We store the
- 23. Dijkstra’s algorithm Review of Priority Queues A Priority Queue is a data structure (can be implemented
- 24. Dijkstra’s algorithm EXTRACT-MIN (Q) removes the vertex in Q with the minimum shortest value and returns
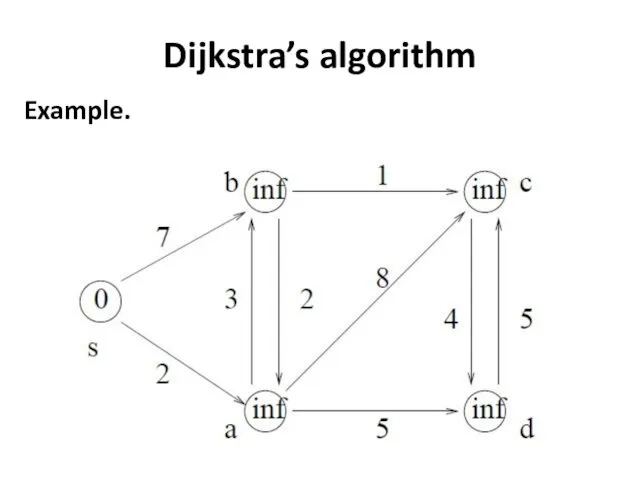
- 25. Dijkstra’s algorithm Example.
- 26. Dijkstra’s algorithm Step 0: Initialization. Priority Queue.
- 27. Dijkstra’s algorithm Step 1: As Adjacent[s]={a,b}, work on a and b and update information. Priority Queue:
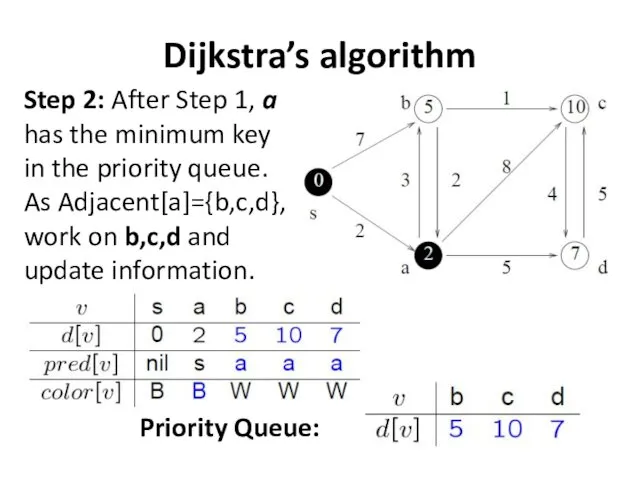
- 28. Dijkstra’s algorithm Step 2: After Step 1, a has the minimum key in the priority queue.
- 29. Dijkstra’s algorithm Step 3: After Step 2, b has the minimum key in the priority queue.
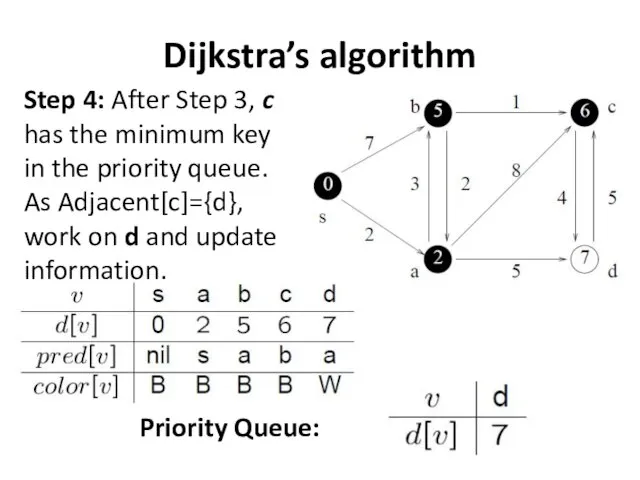
- 30. Dijkstra’s algorithm Step 4: After Step 3, c has the minimum key in the priority queue.
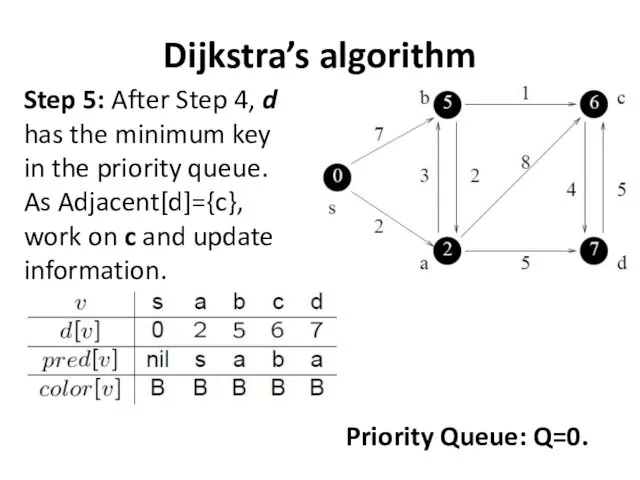
- 31. Dijkstra’s algorithm Step 5: After Step 4, d has the minimum key in the priority queue.
- 32. Dijkstra’s algorithm Shortest Path Tree: T=(V,A), where A={(pred[v],v)|v from V\{s}}. The array pred[v] is used to
- 33. Dijkstra’s algorithm
- 34. Dijkstra’s algorithm Simple array implementation The simplest way to implement the priority queue operations is to
- 35. Dijkstra’s algorithm Simple array implementation The INSERT operation is easy: just add the vertex to the
- 36. Dijkstra’s algorithm Simple array implementation Once we find this vertex, deleting it is easy: just move
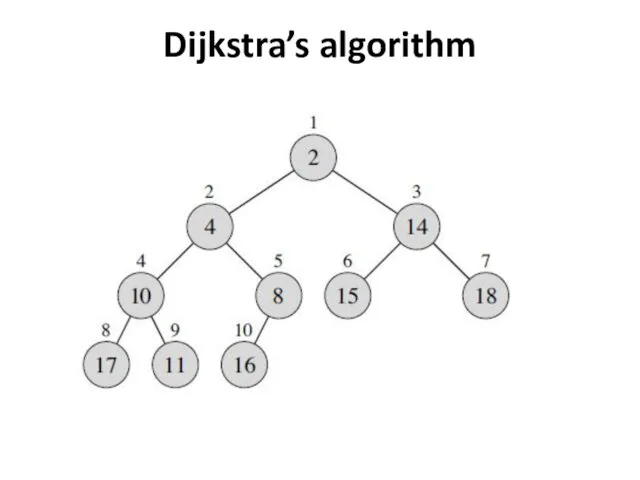
- 37. Dijkstra’s algorithm Binary heap implementation A binary heap organizes data as a binary tree stored in
- 38. Dijkstra’s algorithm
- 39. Dijkstra’s algorithm Nodes with no children, such as nodes 6 through 10, are leaves. A binary
- 40. Dijkstra’s algorithm The node with the minimum key must always be at position 1. The children
- 41. Dijkstra’s algorithm Therefore, we can traverse a path from the root down to a leaf, or
- 43. Скачать презентацию

![Dijkstra’s algorithm the situation at time 0 shortest[s]= 0](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/486175/slide-3.jpg)
![Dijkstra’s algorithm at time 4 shortest[y]= 4, pred[y]= s](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/486175/slide-4.jpg)
![Dijkstra’s algorithm at time 5 shortest[t]=5, pred[t]= y](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/486175/slide-5.jpg)
![Dijkstra’s algorithm at time 7 shortest[z]=7, pred[z]= y](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/486175/slide-6.jpg)
![Dijkstra’s algorithm at time 8 shortest[x]=8, pred[x]=t](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/486175/slide-7.jpg)

















![Dijkstra’s algorithm Step 1: As Adjacent[s]={a,b}, work on a and b and update information. Priority Queue:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/486175/slide-26.jpg)

![Dijkstra’s algorithm Shortest Path Tree: T=(V,A), where A={(pred[v],v)|v from V\{s}}. The](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/486175/slide-31.jpg)








 Аттестационная работа. Рабочая программа математического кружка в 5 классе: Математика плюс
Аттестационная работа. Рабочая программа математического кружка в 5 классе: Математика плюс Постороение сечений
Постороение сечений КАК ГОТОВИТЬСЯ к ГИА-9 по математике Учитель математики Воронина Т.К.
КАК ГОТОВИТЬСЯ к ГИА-9 по математике Учитель математики Воронина Т.К.  Задачи на железнодорожную тему
Задачи на железнодорожную тему Презентация по математике "Теорема косинусов в электронных таблицах" - скачать
Презентация по математике "Теорема косинусов в электронных таблицах" - скачать  Теорема Пифагора
Теорема Пифагора Статистика знает всё
Статистика знает всё Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств Площадь круга
Площадь круга Тема: « Задачи на построение сечений».
Тема: « Задачи на построение сечений».  Призма
Призма Пирамида в задачах ЕГЭ
Пирамида в задачах ЕГЭ Паркеты из многоугольников
Паркеты из многоугольников Касательная. Уравнение касательной
Касательная. Уравнение касательной Вводное повторение.Геометрия 8 класс
Вводное повторение.Геометрия 8 класс Туынды. Алғашқы функция. Интеграл
Туынды. Алғашқы функция. Интеграл Замечательный квадрат. Урок по математике в 5 классе
Замечательный квадрат. Урок по математике в 5 классе Геометрия. 7 класс
Геометрия. 7 класс Фунцияның туындысы мен дифференциалын қолдану
Фунцияның туындысы мен дифференциалын қолдану Линейные дискретные системы. Описание ЛДС во временной области
Линейные дискретные системы. Описание ЛДС во временной области Общая математическая модель динамики
Общая математическая модель динамики Подготовка к ГИА по математике. Задания 13
Подготовка к ГИА по математике. Задания 13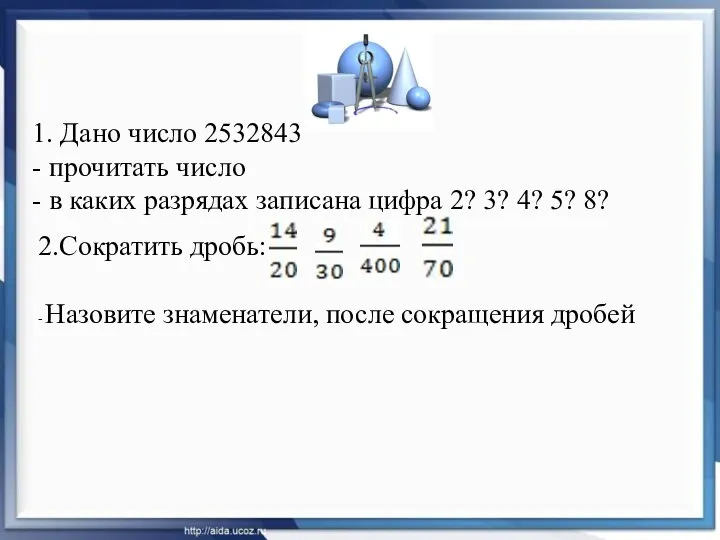 Как записывают и читают десятичные дроби
Как записывают и читают десятичные дроби Решение неравенств
Решение неравенств Объемы тел
Объемы тел Изучение взаимосвязи между явлениями методами корреляционно-регрессионного анализа
Изучение взаимосвязи между явлениями методами корреляционно-регрессионного анализа Геометрические иллюзии, или всегда ли мы видим то, что видим
Геометрические иллюзии, или всегда ли мы видим то, что видим Что такое процент
Что такое процент