Содержание
- 2. Use the Rational Zero Theorem to find possible rational zeros. Find zeros of a polynomial function.
- 3. The Rational Zero Theorem If has integer coefficients and (where is reduced to lowest terms) is
- 4. Example: Using the Rational Zero Theorem List all possible rational zeros of The constant term is
- 5. Example: Finding Zeros of a Polynomial Function Find all zeros of We begin by listing all
- 6. Example: Finding Zeros of a Polynomial Function (continued) Find all zeros of Possible rational zeros are
- 7. Example: Finding Zeros of a Polynomial Function (continued) Find all zeros of Possible rational zeros are
- 8. Example: Finding Zeros of a Polynomial Function (continued) Find all zeros of We have found a
- 9. Example: Finding Zeros of a Polynomial Function (continued) Find all zeros of We have found that
- 10. Properties of Roots of Polynomial Equations 1. If a polynomial equation is of degree n, then
- 11. Example: Solving a Polynomial Equation Solve We begin by listing all possible rational roots: Possible rational
- 12. Example: Solving a Polynomial Equation (continued) Solve Possible rational roots are 1, –1, 13, and –13.
- 13. Example: Solving a Polynomial Equation (continued) Solve We have found that x = 1 is a
- 14. Example: Solving a Polynomial Equation (continued) Solve Possible rational roots are 1, –1, 13, and –13.
- 15. Example: Solving a Polynomial Equation (continued) Solve The factored form of this polynomial is We will
- 16. The Fundamental Theorem of Algebra If f(x) is a polynomial of degree n, where then the
- 17. The Linear Factorization Theorem If where and then where c1, c2, ..., cn are complex numbers
- 18. Example: Finding a Polynomial Function with Given Zeros Find a third-degree polynomial function f(x) with real
- 19. Example: Finding a Polynomial Function with Given Zeros Find a third-degree polynomial function f(x) with real
- 20. Descartes’ Rule of Signs Let be a polynomial with real coefficients. 1. The number of positive
- 21. Descartes’ Rule of Signs (continued) Let be a polynomial with real coefficients. 2. The number of
- 22. Example: Using Descartes’ Rule of Signs Determine the possible number of positive and negative real zeros
- 24. Скачать презентацию





















 Теорія множин. Відношення
Теорія множин. Відношення Презентация на тему Морской пейзаж
Презентация на тему Морской пейзаж Обыкновенные дроби. (Урок 48)
Обыкновенные дроби. (Урок 48) Теорема Пифагора
Теорема Пифагора Математическая викторина
Математическая викторина Методика изучения площади
Методика изучения площади Презентация по математике "Программа для работы с тригонометрическими функциями" - скачать
Презентация по математике "Программа для работы с тригонометрическими функциями" - скачать  XX ғасырдағы математиканың дамуының өзіндік ерекшеліктері
XX ғасырдағы математиканың дамуының өзіндік ерекшеліктері Корреляционный анализ
Корреляционный анализ Устойчивость сжатых стержней (продольный изгиб). Формула Эйлера
Устойчивость сжатых стержней (продольный изгиб). Формула Эйлера Симметрия в природе
Симметрия в природе Метод парных сравнений
Метод парных сравнений Справочные материалы. Множественная регрессия, тестирование предпосылок
Справочные материалы. Множественная регрессия, тестирование предпосылок Отношения и функции
Отношения и функции Некоторые часто встречающиеся дискретные распределения
Некоторые часто встречающиеся дискретные распределения Сопряжение. Центр сопряжения. Точки сопряжения
Сопряжение. Центр сопряжения. Точки сопряжения Смотр знаний по математике «Умники и умницы» (7 класс)
Смотр знаний по математике «Умники и умницы» (7 класс) Алгебраические фракталы
Алгебраические фракталы Алгебраические уравнения произвольных степеней
Алгебраические уравнения произвольных степеней  Период математического маятника
Период математического маятника Координатная плоскость. Умножение и деление обыкновенных дробей
Координатная плоскость. Умножение и деление обыкновенных дробей Прочитай число. Повторение
Прочитай число. Повторение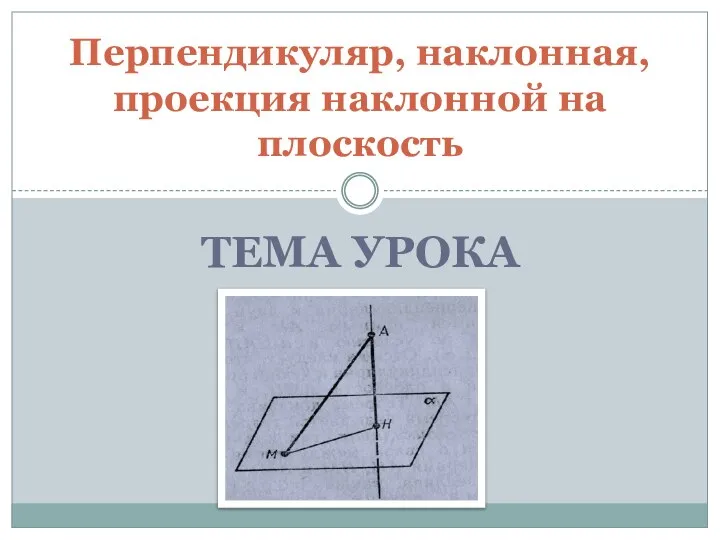 Перпендикуляр, наклонная, проекция наклонной на плоскость Тема урока
Перпендикуляр, наклонная, проекция наклонной на плоскость Тема урока  Презентация по математике "Переместительное свойство умножения" - скачать бесплатно
Презентация по математике "Переместительное свойство умножения" - скачать бесплатно Учимся решать задачи на движение
Учимся решать задачи на движение Презентация по математике "Функция у=ах^2, её свойства и график" - скачать бесплатно
Презентация по математике "Функция у=ах^2, её свойства и график" - скачать бесплатно Презентация по математике "Интегралы" - скачать
Презентация по математике "Интегралы" - скачать  Архитектура и геометрия
Архитектура и геометрия