Содержание
- 3. Частные производные высших порядков Т.е. Замечание:
- 4. Дифференциал функции нескольких переменных Определение. Дифференциалом функции нескольких переменных называется сумма произведений частных производных этой функции
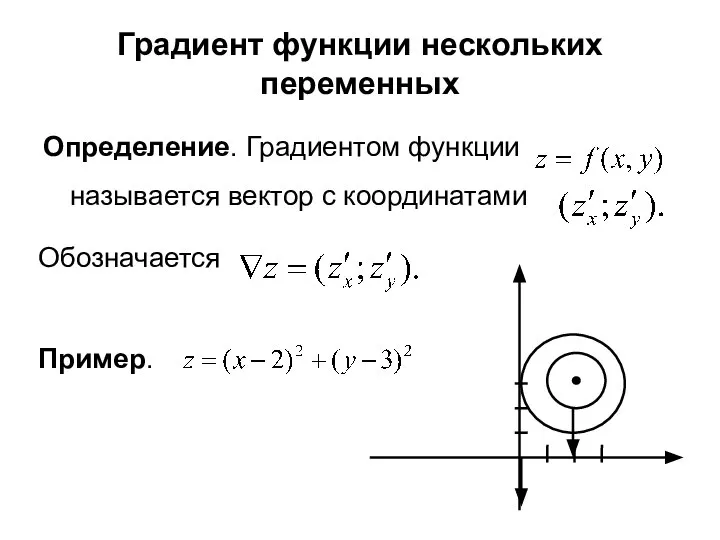
- 5. Градиент функции нескольких переменных Определение. Градиентом функции называется вектор с координатами Обозначается Пример.
- 6. Экстремум функции нескольких переменных. Определение. Пусть функция z=f (x; y) определена на множестве D⊂R2. Точка M(x0;y0)
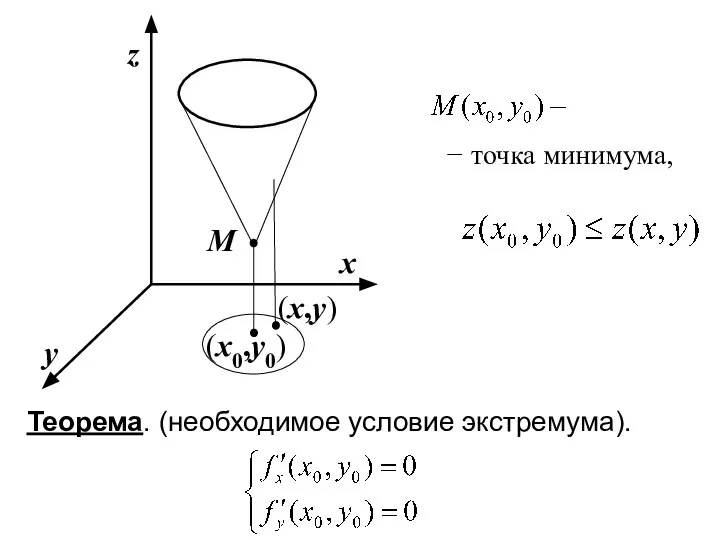
- 7. − точка минимума, Теорема. (необходимое условие экстремума).
- 8. называются критическими или стационарными. Замечание: Точки, в которых выполнены необходимые условия экстремума функции z=f (x; y),
- 9. Пример. но существует точка (1,−1) такая, что z( 1,−1)=−1 или точка (2,3) такая, что z(2,3)=6>z(0,0). Следовательно,
- 10. Пример.
- 11. Теорема. (достаточное условие экстремума функции 2-х переменных). Пусть функция а) определена в некоторой окрестности критической точки
- 12. Тогда: если и А>0, то это min, то в точке (x0;y0) существует экстремум, причем если и
- 13. Схема исследования функции на экстремум 1. Определить область определения функции 2. Найти и и решить систему
- 14. Пример. или или Таким образом − критические точки. 1. 2.
- 15. 3. Для точки Следовательно, нужны дополнительные исследования. Следовательно, точка является точкой максимума. Для точки 4.
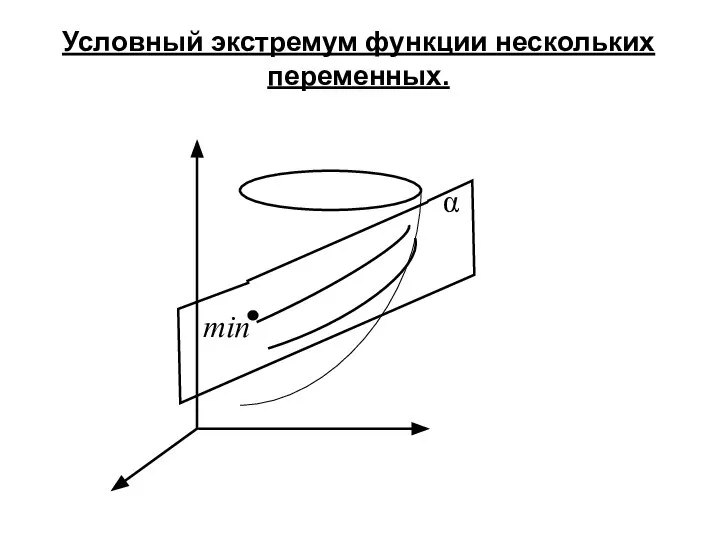
- 16. Условный экстремум функции нескольких переменных.
- 17. Определение. Точка (x0; y0) называется точкой условного максимума (минимума) функции z=f (x;y), если существует такая окрестность
- 18. Пример. 1 способ. 2 способ. Метод Лагранжа. Строим функцию Лагранжа:
- 20. Скачать презентацию













 Генетический подход в изучении геометрии
Генетический подход в изучении геометрии Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Золотое сечение
Золотое сечение Формулы сокращенного умножения
Формулы сокращенного умножения Презентация "Математики"
Презентация "Математики" Метод координат
Метод координат Формула разности квадратов. 7 класс
Формула разности квадратов. 7 класс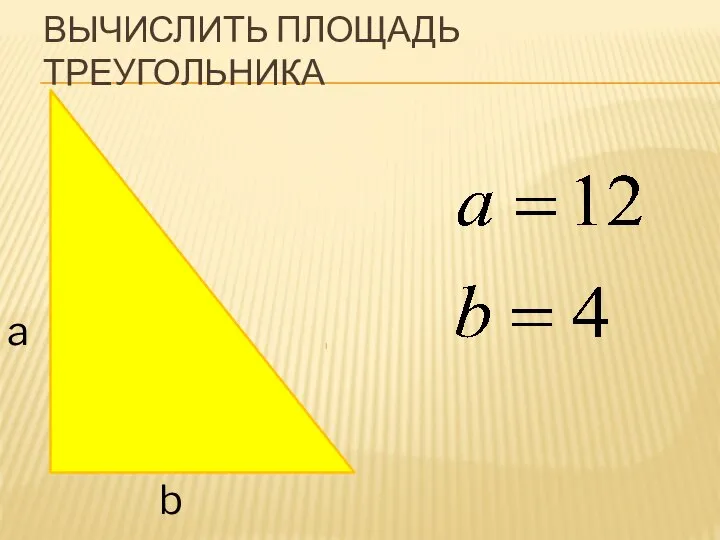 Вычисление площади треугольника
Вычисление площади треугольника Теория вероятностей
Теория вероятностей Математика Л. Г. Петерсон, 2 класс Устный счет по теме «Многозначные числа»
Математика Л. Г. Петерсон, 2 класс Устный счет по теме «Многозначные числа» Простейшие задачи в координатах
Простейшие задачи в координатах Геометрическая прогрессия. Урок 1
Геометрическая прогрессия. Урок 1 Математика – царица наук. Умножение на 1 и 0
Математика – царица наук. Умножение на 1 и 0 Неравенство треугольника
Неравенство треугольника Квадратичная функция. 9 класс
Квадратичная функция. 9 класс Повторение по математике
Повторение по математике Способы вычисления неопределенных интегралов (лекция 26)
Способы вычисления неопределенных интегралов (лекция 26) Задачи практического характера в разных областях науки и техники
Задачи практического характера в разных областях науки и техники Теория вероятностей, математическая статистика и случайные процессы
Теория вероятностей, математическая статистика и случайные процессы Решение задач на проценты
Решение задач на проценты 20161216_den_fibonachchi
20161216_den_fibonachchi Презентация по математике "Вычитание" - скачать бесплатно
Презентация по математике "Вычитание" - скачать бесплатно Вычитание векторов. Умножение вектора на число
Вычитание векторов. Умножение вектора на число Проценты
Проценты Зерттеудің нәтижелерін. Талдау
Зерттеудің нәтижелерін. Талдау Интерактивная игра-тренажёр по теме: «Сложение и вычитание в пределах 20» Математика 2 класс
Интерактивная игра-тренажёр по теме: «Сложение и вычитание в пределах 20» Математика 2 класс  Средние величины в статистике
Средние величины в статистике Реализация деятельностного подхода на уроках математики.
Реализация деятельностного подхода на уроках математики.