Содержание
- 4. Числовые неравенства Неравенство называется числовым, когда каждая из его частей обозначает некоторое число. Числовое неравенство А
- 5. х больше 9, но меньше 18
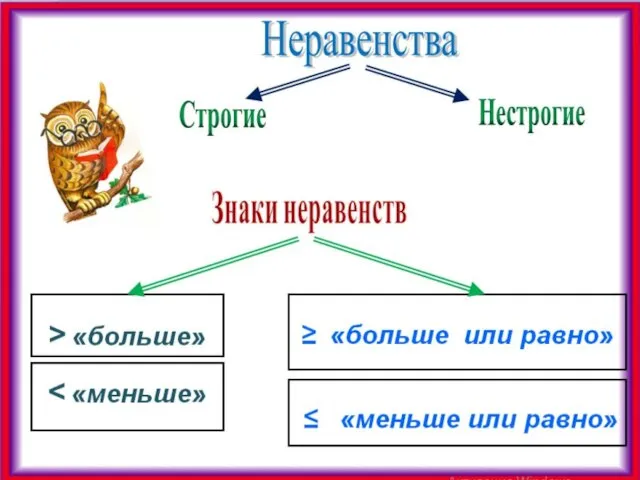
- 8. Определение Говорят, что действительное число а больше (меньше) действительного числа в, если их разность (а-в)- положительное
- 9. Строгие неравенства а > 0 означает, что а– положительное число а а > в означает, что
- 10. Нестрогие неравенства а ≥ 0 означает, что а больше нуля или равно нулю, т.е. а –
- 11. Нестрогие неравенства а ≥ в означает, что а больше в или равно в, т.е. а-в –
- 13. Свойства числовых неравенств
- 15. 1 свойство (транзитивность) Теорема Если а > b и b > c, то а > c.
- 16. 1 свойство Теорема Если а Если точка а расположена левее точки b, а точка b расположена
- 17. Теорема. Если к обеим частям верного числового неравенства прибавить одно и то же число или из
- 19. Теорема Если обе части верного числового неравенства умножить или разделить на одно и то же положительное
- 20. Следствие Если а и b – числа одного знака и а 3 -7, значит значит 5
- 21. Теорема Если обе части верного числового неравенства умножить или разделить на одно и то же отрицательное
- 28. Письменно Мордкович №31.1 - 31.19 все нечетные номера под буквами в) и г).
- 29. Применение свойств неравенств Пусть р (р – с)7 (р – с)6 Так как 6 – четное
- 30. Сложение числовых неравенств Теорема. Если а Если а > b и с > d, то а
- 31. Умножение числовых неравенств Теорема. Если а, b, с, d – положительные числа и а а если
- 32. Возведение неравенств в натуральную степень Следствие. Пусть а > 0, b > 0 и n N,
- 34. Скачать презентацию






























 Математика в жизни человека
Математика в жизни человека Интерактивный тест. Готовимся к ОГЭ. 2 вариант
Интерактивный тест. Готовимся к ОГЭ. 2 вариант Мера центральной тенденции. Средние величины и изучение вариации
Мера центральной тенденции. Средние величины и изучение вариации Сложение обыкновенных дробей. Графический диктант 4. 5 класс
Сложение обыкновенных дробей. Графический диктант 4. 5 класс Проверка правильности логического рассуждения
Проверка правильности логического рассуждения Нумерация чисел от 1 до 100. Тест
Нумерация чисел от 1 до 100. Тест Две окружности на плоскости
Две окружности на плоскости Функция у=кх², ее свойства и график
Функция у=кх², ее свойства и график Матдрака 2011. Математический фестиваль
Матдрака 2011. Математический фестиваль Окружности, описанные и вписанные в правильные многоугольники
Окружности, описанные и вписанные в правильные многоугольники Двугранный угол
Двугранный угол Действия с векторами
Действия с векторами Устный счет
Устный счет Задачи на построение
Задачи на построение Общие сведения из теории графов
Общие сведения из теории графов Примеры комбинаторных задач
Примеры комбинаторных задач Движение плоскости. (9 класс)
Движение плоскости. (9 класс) Определенный интеграл
Определенный интеграл Методы оптимальных решений в линейном программировании
Методы оптимальных решений в линейном программировании Применение производной в химии и биологии
Применение производной в химии и биологии Средние величины
Средние величины Презентация на тему Занимательные задачи по математике
Презентация на тему Занимательные задачи по математике  Площади фигур
Площади фигур Вычисление площади многоугольника
Вычисление площади многоугольника Деление трехзначного числа на двухзначное
Деление трехзначного числа на двухзначное Функция у х, её свойства и график
Функция у х, её свойства и график Auctions. (Lecture 10)
Auctions. (Lecture 10) Смежные и вертикальные углы
Смежные и вертикальные углы