Содержание
- 2. ОБЩАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Общая задача математического программирования: найти экстремум целевой функции F(X) =f (х1, х2,
- 3. Если целевая функция (1.1) и система ограничений (1.2) линейны, то задача математического программирования называется задачей линейного
- 4. F(X) = с1 х1 + с2 х2 + ... + сп хп→max,
- 5. В задаче на нахождение минимального значения целевой функции математическая модель её запишется в виде F(X) =
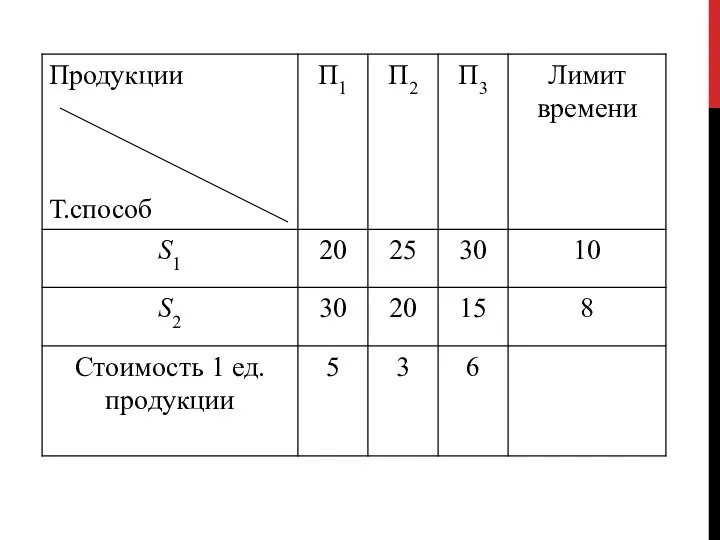
- 6. РАССМОТРИМ ВАРИАНТЫ СОСТАВЛЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЛЯ СЛЕДУЮЩИХ ЗАДАЧ Задача 1. (Планирование производства.) Некоторое предприятие выпускает три
- 8. Необходимо так организовывать производство, чтобы получить наибольшую прибыль при реализации продукции по указанной стоимости.
- 9. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЗАДАЧИ Обозначим через хi j — время, затраченное на изготовление продукции Пj (j =
- 10. При этом продукции 1-го вида будет выпущено 20х11+ 30х21 , 2-го вида 25х12+20х22 , 3-го вида
- 11. ОКОНЧАТЕЛЬНО ПОЛУЧАЕМ МАТЕМАТИЧЕСКУЮ МОДЕЛЬ ЗАДАЧИ F=5(20х11+ 30х21)+3(25х12+20х22)+6(30х13+ 15х23) → max,
- 12. ЗАДАЧА 2. (ЗАДАЧА О СМЕСИ.) Известно, что при правильном питании человек должен получать в день не
- 14. Математическая модель задачи Пусть хi — количество продукта Пi, потребляемого в день (i=1,2,3), тогда стоимость всех
- 15. F=25х1 +30x2 +20х3 → min,
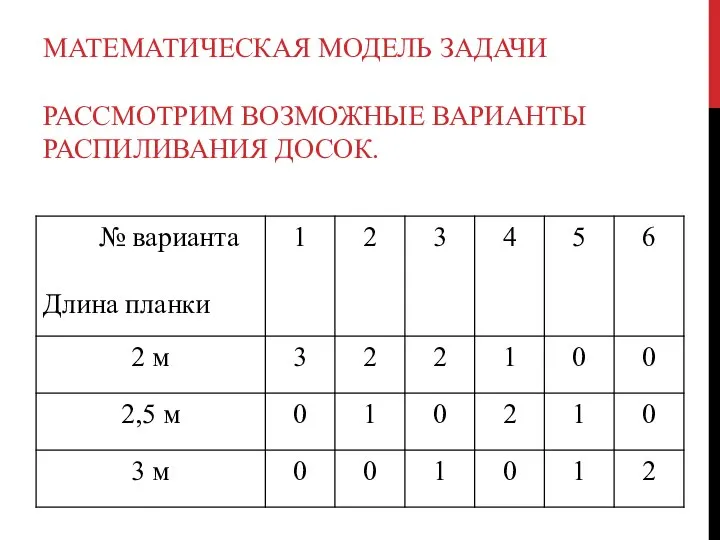
- 16. ЗАДАЧА 3. (О РАСКРОЕ МАТЕРИАЛА.) Для изготовления некоторого изделия требуется 2 планки по 2 м, 3
- 17. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЗАДАЧИ РАССМОТРИМ ВОЗМОЖНЫЕ ВАРИАНТЫ РАСПИЛИВАНИЯ ДОСОК.
- 18. Обозначим через хi— количество досок, распиленных i-м способом, тогда заготовок по 2 м получится 3x1+ 2х2
- 19. х 3 + x5 + 2x6=к. Исключим к. 2(3x1+ 2х2 + 2х3 + х4 )= 3(x2
- 20. Окончательно получим математическую модель к=х 3 + x5 + 2x6→ max, все хi ≥0.
- 21. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Задача с двумя переменными Пусть требуется найти максимальное значение функции
- 22. Алгоритм решения ЗЛП с двумя переменными графическим методом: Строится область допустимых решений. Строится вектор = (с1,
- 23. Пример 1. Решить задачу линейного программирования графическим методом: F(X)=2x1+4x2→ max,
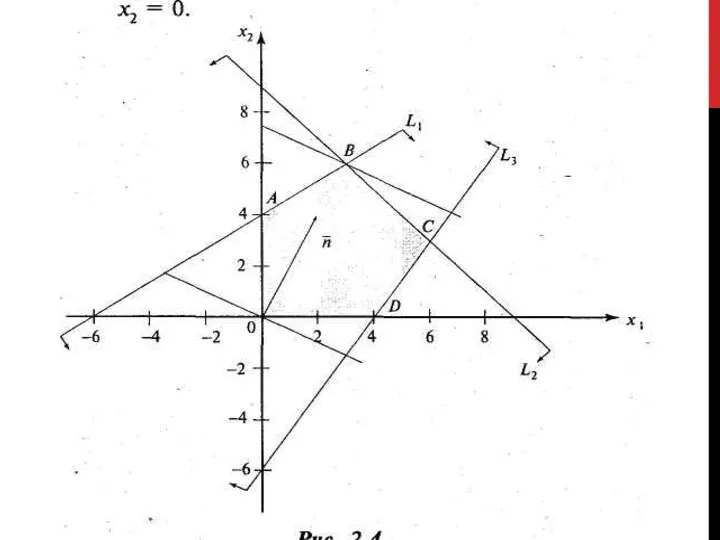
- 24. Решение. Изобразим на плоскости систему координат Ох1х2 и построим граничные прямые области допустимых решений (номера прямых
- 25. Перпендикулярно вектору построим одну из линий уровня (на рис. она проходит через начало координат). Так как
- 27. В данном случае опорной прямой является прямая, проходящая через точку пересечения граничных прямых L1 и L2,
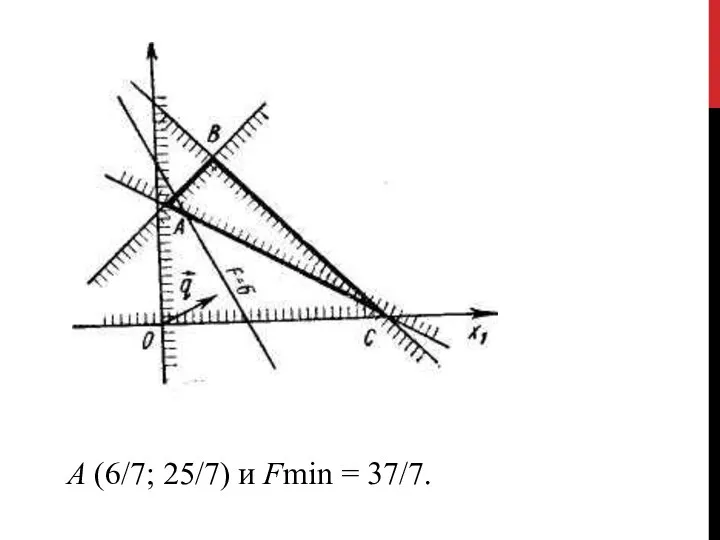
- 28. Пример 2. Найти минимум функции F(X)=2x1+x2→ min при ограничениях
- 29. А (6/7; 25/7) и Fmin = 37/7.
- 30. ДВОЙСТВЕННАЯ ЗАДАЧА В теории двойственности используются четыре пары двойственных задач (приведем их в матричной форме записи):
- 31. Исходная задача Двойственная задача Симметричные пары 1. F(X)=CX→max, Z(Y)=YA0→min AX≤ A0 , YA≥ C, X≥θ; Y≥θ.
- 32. Несимметричные пары 1. F(X)=CX→max, Z(Y)=YA0→min AX= A0 , YA≥ C. X≥θ; 2. F(X)=CX→min, Z(Y)=YA0→ max, AX=A0
- 33. Здесь С=(с1, с2,…, сn), Y= (у1, у2,… …,ут),
- 34. Пример 1. Составить задачу, двойственную к данной F(X) = х1 + 4х2 +3 х3→min,
- 35. Решение. Умножим первое ограничение-неравенство на -1. Задача примет вид исходной задачи симметричной пары двойственных задач: F(X)
- 36. Окончательно двойственная задача имеет вид Z(Y) = -10у1 + 6у2 + 12у3→ max,
- 37. Первая теорема двойственности Теорема. Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная
- 38. Вторая теорема двойственности Пусть имеется симметричная пара двойственных задач
- 39. Теорема. Для того чтобы допустимые решения Х= (х1, х2, ..., хп), Y=(y1, y2, ..., yт) являлись
- 40. Пример 1. Для данной задачи составить двойственную, решить ее графическим методом и, используя вторую теорему двойственности,
- 41. Решение. Составим двойственную задачу: Z(Y) = 2у1 + 3у2→ max,
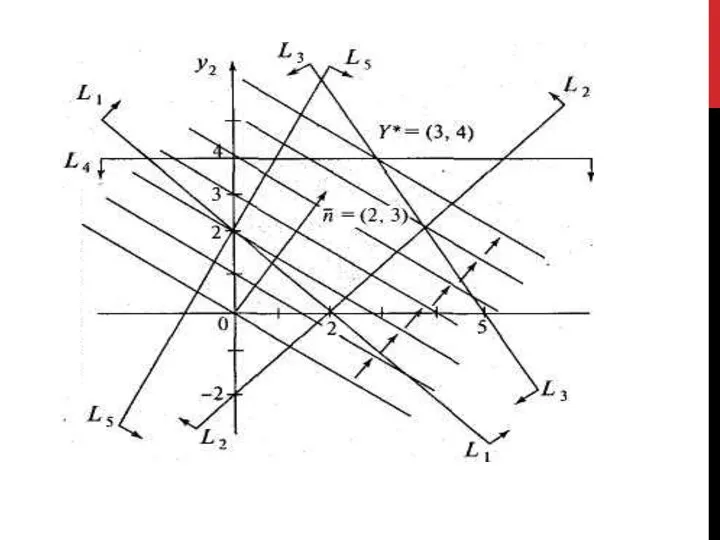
- 42. Решим эту задачу графическим методом. На рис. изображены область допустимых решений задачи, нормаль п = (2,
- 44. 2у1=6 у1*=3, у2*=4. Y *=(3,4). Z(Y *)=2·3+3·4=18.
- 45. Подставим оптимальное решение Y *= (3, 4) в систему ограничений. Получим, что первое, второе и пятое
- 46. По второй теореме двойственности следует, что соответствующие координаты оптимального решения двойственной задачи, т.е. исходной задачи, равны
- 47. Отсюда находим х3*= 1, х4* = 2. Окончательно записываем X*=(0,0,1,2,0). Ответ: min F(X) = 18 при
- 48. ТРАНСПОРТНАЯ ЗАДАЧА Формулировка транспортной задачи Однородный груз сосредоточен у т поставщиков в объемах a1, a2,..., ат.
- 50. Исходные данные задачи могут быть представлены также в виде вектора запасов поставщиков А=(a1,a2,...,ат), вектора запросов потребителей
- 52. ОПОРНОЕ РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ
- 53. Свойство системы ограничений транспортной задачи: ранг системы векторов ― условий транспортной задачи равен N=т + п
- 54. Клетки таблицы транспортной задачи, в которых находятся отличные от нуля или базисные нулевые перевозки, называются занятыми,
- 57. МЕТОДЫ ПОСТРОЕНИЯ НАЧАЛЬНОГО ОПОРНОГО РЕШЕНИЯ МЕТОД СЕВЕРО-ЗАПАДНОГО УГЛА Существует ряд методов построения начального опорного решения, наиболее
- 58. Во избежание ошибок после построения начального опорного решения необходимо проверить, что число занятых клеток равно т
- 61. ПЕРЕХОД ОТ ОДНОГО ОПОРНОГО РЕШЕНИЯ К ДРУГОМУ В транспортной задаче переход от одного опорного решения к
- 62. Теорема (о существовании и единственности цикла). Если таблица транспортной задачи содержит опорное решение, то для любой
- 64. Сдвигом по циклу на величину θ называется увеличение объемов перевозок во всех нечетных клетках цикла, отмеченных
- 65. МЕТОД ПОТЕНЦИАЛОВ
- 67. Числа Δij называются оценками свободных клеток таблицы или векторов ― условий транспортной задачи,
- 69. ОСОБЕННОСТИ РЕШЕНИЯ ТРАНСПОРТНЫХ ЗАДАЧ С НЕПРАВИЛЬНЫМ БАЛАНСОМ
- 70. Следовательно, чтобы задача в рассматриваемом случае имела решение, необходимо ввести фиктивного потребителя с запросами bn+1, равными
- 72. Следовательно, чтобы в этом случае задача имела решение, необходимо ввести фиктивного поставщика с запасами ат+1, равными
- 73. Алгоритм решения транспортной задачи методом потенциалов Проверяют выполнение необходимого и достаточного условия разрешимости задачи. Если задача
- 74. 3.Строят систему потенциалов, соответствующих опорному решению. Для этого решают систему уравнений Для того чтобы найти частное
- 75. при если известен потенциал .
- 76. 4. Проверяют, выполняется ли условие оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех
- 77. 5. Переходят к новому опорному решению, на котором значение целевой функции будет меньше. Для этого находят
- 78. Строят цикл, включающий в свой состав данную клетку и часть клеток, занятых опорным решением. В клетках
- 79. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют
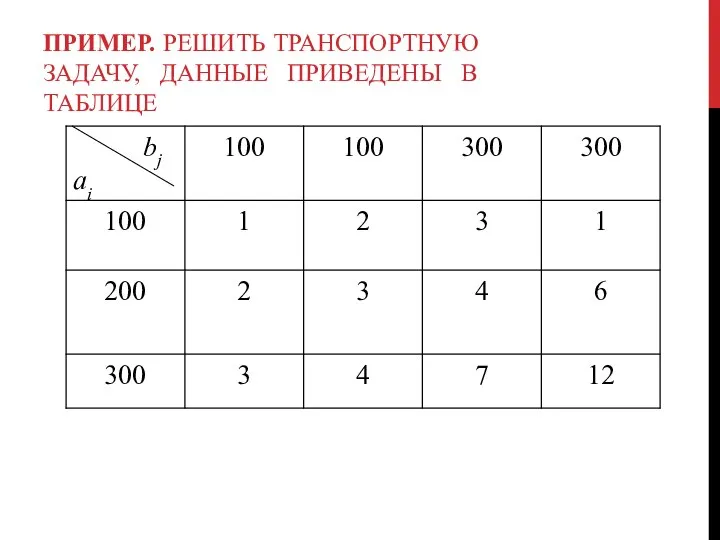
- 80. ПРИМЕР. РЕШИТЬ ТРАНСПОРТНУЮ ЗАДАЧУ, ДАННЫЕ ПРИВЕДЕНЫ В ТАБЛИЦЕ
- 81. Решение. 1. Проверяем выполнение необходимого и достаточного условия разрешимости задачи. Находим суммарные запасы поставщиков и запросы
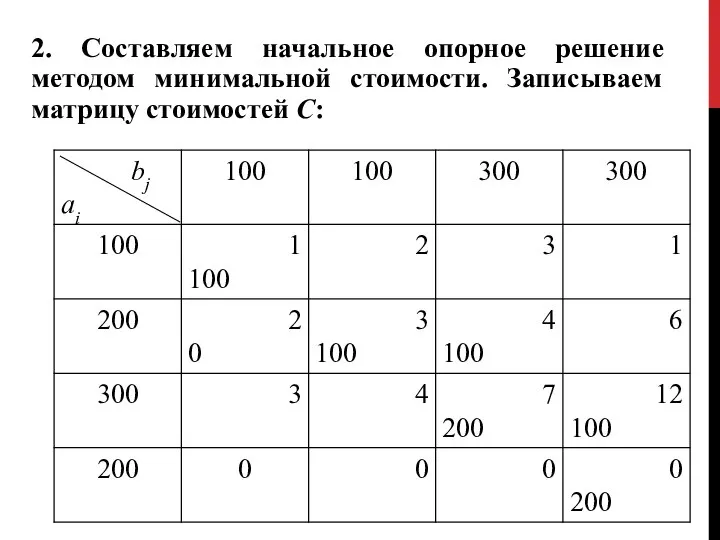
- 82. 2. Составляем начальное опорное решение методом минимальной стоимости. Записываем матрицу стоимостей С:
- 83. Полученное решение Х1 имеет т + п — 1=4 + 4 — 1 = 7 базисных
- 84. 3. Для проверки оптимальности опорного решения необходимо найти потенциалы. По признаку оптимальности в каждой занятой опорным
- 86. Система состоит из семи уравнений и имеет восемь переменных. Система неопределенная. Одному из потенциалов задаем значение
- 88. 4. Проверяем опорное решение Х1 на оптимальность. С этой целью вычисляем оценки для всех незаполненных клеток
- 90. 5. Переходим к новому опорному решению. Находим клетку таблицы, которой соответствует наибольшая положительная оценка: для клетки
- 91. Х1 bj v1=2 v2=3 v3=4 v4=9
- 92. Положительные оценки записываем в левые нижние углы соответствующих клеток таблицы, вместо отрицательных ставим знак «—». Начальное
- 93. В данном случае минимум перевозок в клетках, отмеченных знаком «-», достигался сразу в трех клетках, поэтому
- 94. 6. Проверяем второе опорное решение Х2 на оптимальность. Находим, потенциалы и оценки. Решение не является оптимальным,
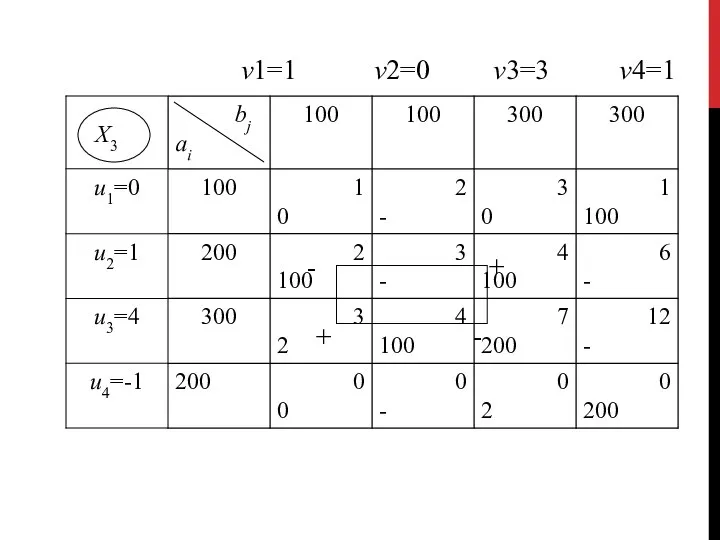
- 95. v1=1 v2=0 v3=3 v4=1 Х3
- 96. Вычисляем значение целевой функции на третьем опорном решении: F(X3)= 0·1 + 100·1 + 100·2 + 100·4
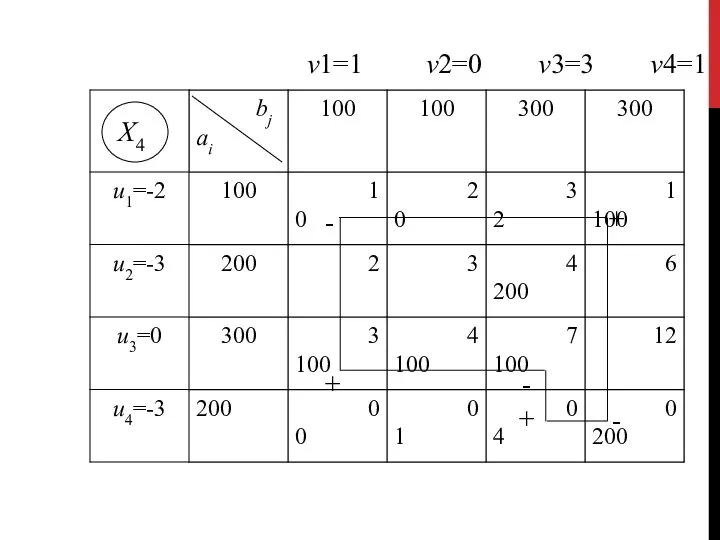
- 97. v1=1 v2=0 v3=3 v4=1 Х4
- 98. Вычисляем значение целевой функции на четвертом опорном решении: F(Х4) = 0·l + 100·1 +200·4+ 100·3 +
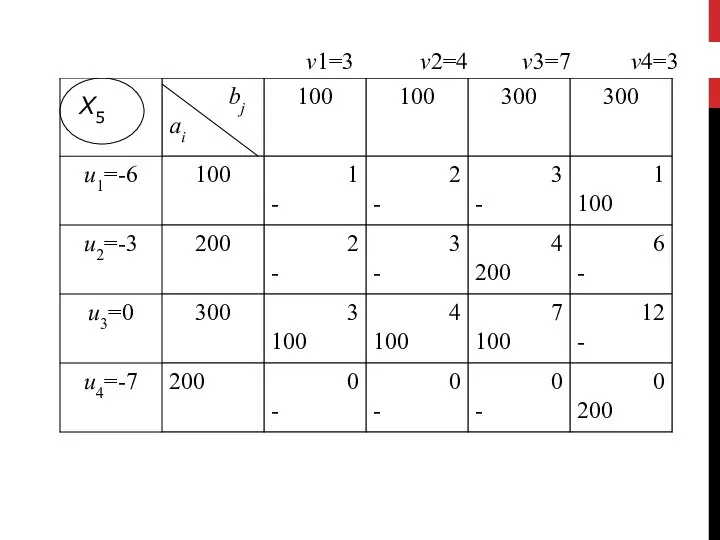
- 99. Х5 v1=3 v2=4 v3=7 v4=3
- 101. Скачать презентацию


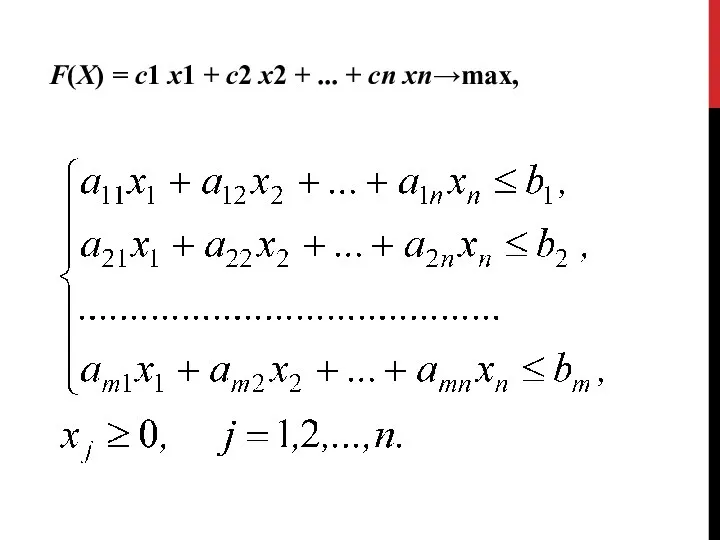









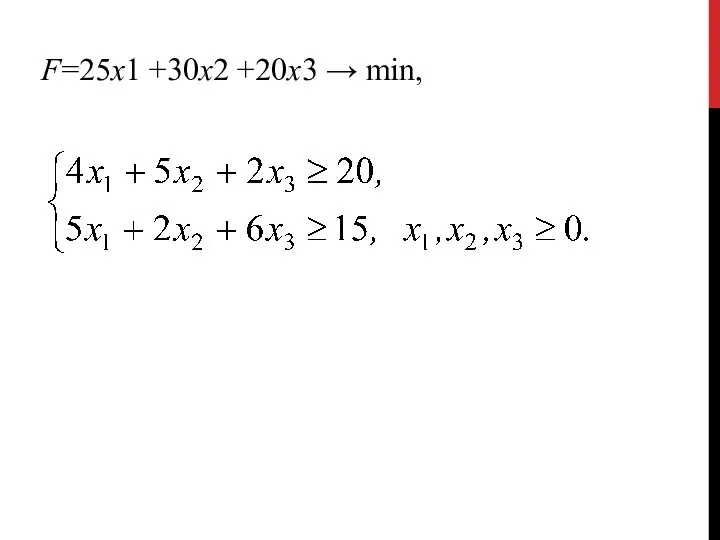


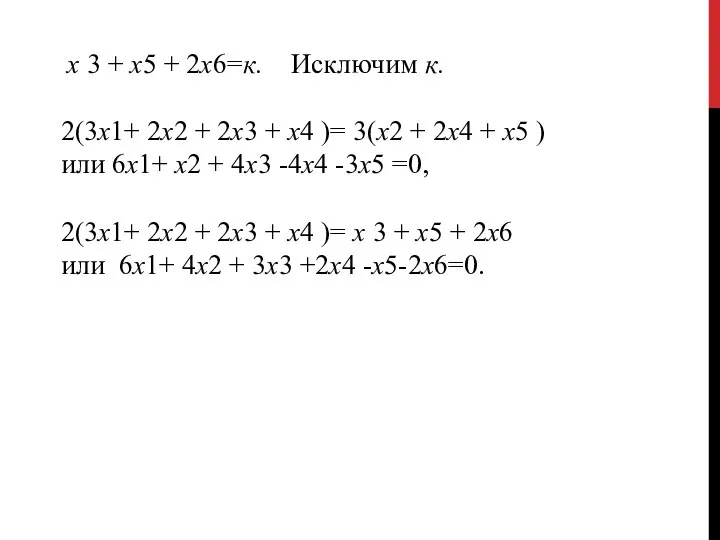
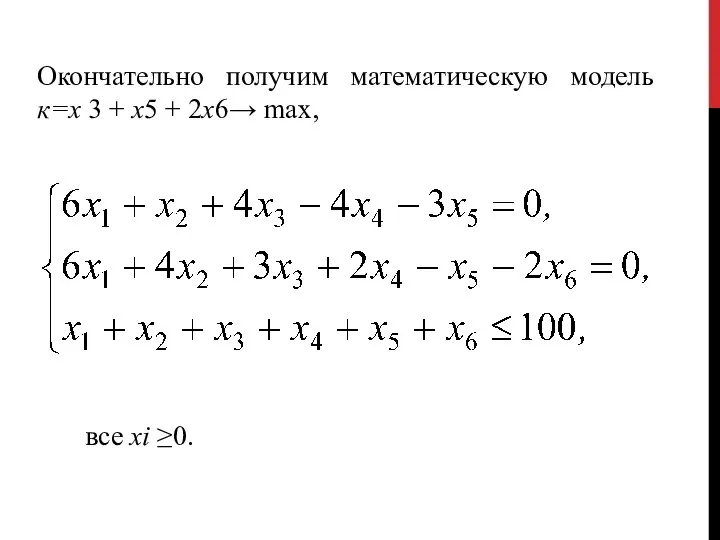











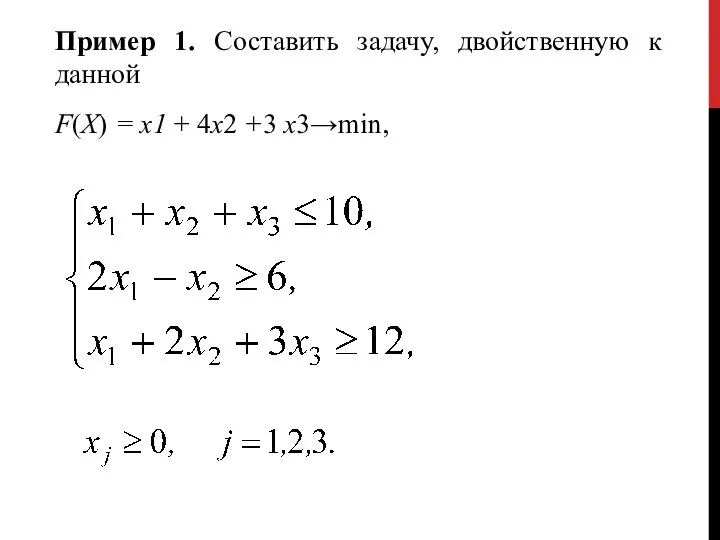








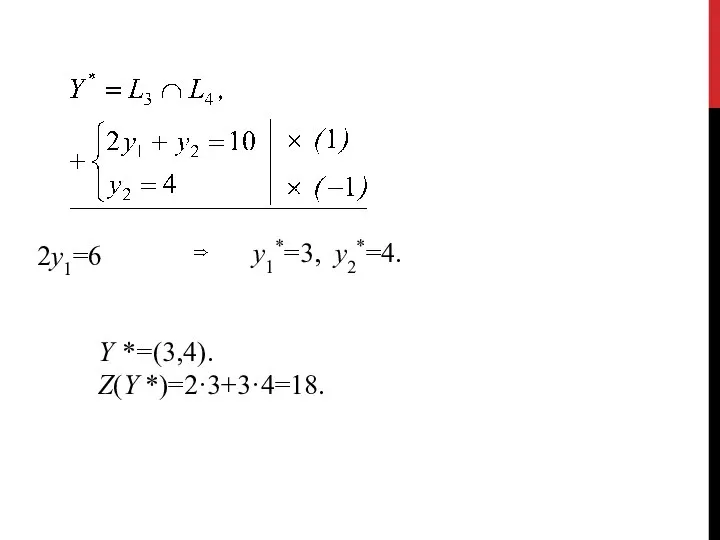






































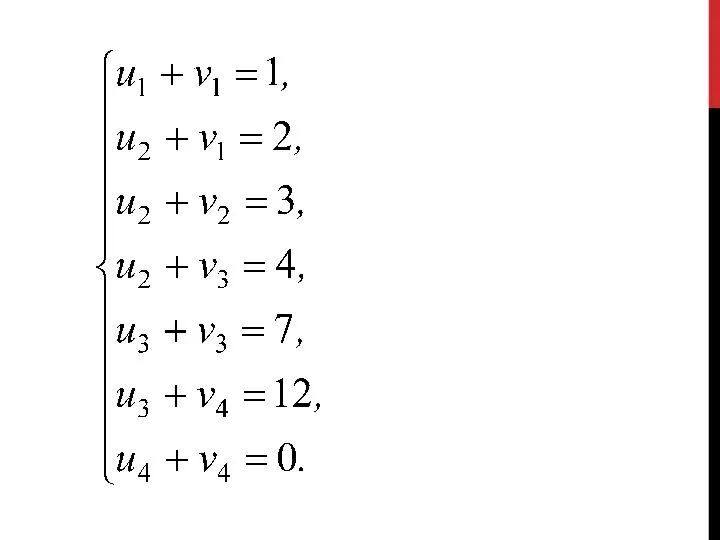

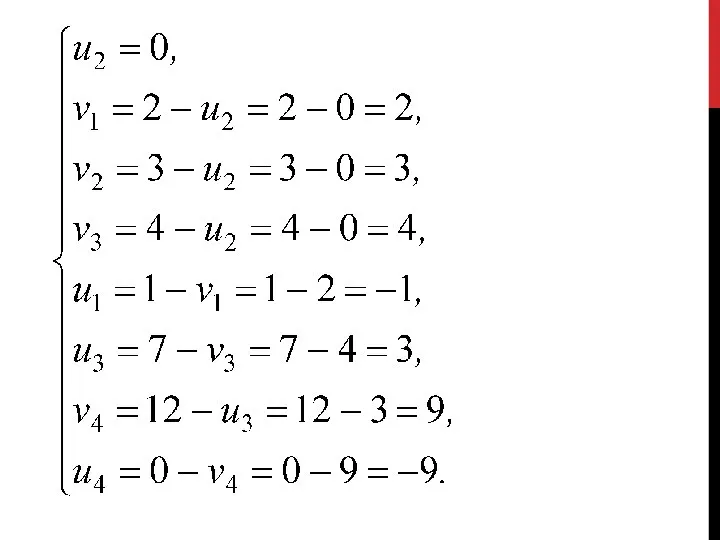









 Основное свойство дроби Математика, 6 класс Учитель Гончаров О. Н.
Основное свойство дроби Математика, 6 класс Учитель Гончаров О. Н.  Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников УРОК МАТЕМАТИКИ 6 КЛАСС «Нахождение числа по его дроби»
УРОК МАТЕМАТИКИ 6 КЛАСС «Нахождение числа по его дроби»  Арккосинус и решение уравнения cos x = a Уроки № 1-2
Арккосинус и решение уравнения cos x = a Уроки № 1-2 Правильные многоугольники в нашей жизни
Правильные многоугольники в нашей жизни Числовые промежутки. 8 класс
Числовые промежутки. 8 класс Арифметическая прогрессия
Арифметическая прогрессия Случаи сложения и вычитания основанные на знаниях нумерации. Урок №92
Случаи сложения и вычитания основанные на знаниях нумерации. Урок №92 Умножение нуля и единицы
Умножение нуля и единицы Решение заданий В11 (часть 1) по материалам открытого банка задач ЕГЭ по математике 2013 года
Решение заданий В11 (часть 1) по материалам открытого банка задач ЕГЭ по математике 2013 года Теорема Вариньона и ее применение. 9 класс
Теорема Вариньона и ее применение. 9 класс Начальные условия. Граничные условия
Начальные условия. Граничные условия Презентация по математике "Дециметр - единица измерения длины" - скачать бесплатно
Презентация по математике "Дециметр - единица измерения длины" - скачать бесплатно Математика. Профильный уровень. ЕГЭ
Математика. Профильный уровень. ЕГЭ Решение задач
Решение задач Призмы и антипризмы
Призмы и антипризмы Координатная плоскость (задачи)
Координатная плоскость (задачи) Презентация по математике "ТАБЛИЦА УМНОЖЕНИЯ НА 2 И 3" - скачать бесплатно
Презентация по математике "ТАБЛИЦА УМНОЖЕНИЯ НА 2 И 3" - скачать бесплатно Презентация по математике "Площадь Единицы площади" - скачать
Презентация по математике "Площадь Единицы площади" - скачать  Своя игра. Степень с натуральным показателем
Своя игра. Степень с натуральным показателем Нахождения дроби от числа, числа по его дроби ( 6 класс)
Нахождения дроби от числа, числа по его дроби ( 6 класс) Кривые второго порядка
Кривые второго порядка Законы сложения и вычитания 5 класс
Законы сложения и вычитания 5 класс Решение задач к экзамену. Весенний семестр
Решение задач к экзамену. Весенний семестр График квадратичной функции. Неравенства с одной переменной
График квадратичной функции. Неравенства с одной переменной Презентация урока математики в 5 классе по теме: «Деление десятичной дроби на натуральное число» г. Кемерово МОУ «Гимназия № 4
Презентация урока математики в 5 классе по теме: «Деление десятичной дроби на натуральное число» г. Кемерово МОУ «Гимназия № 4 Показательные неравенства. Решение простейшего показательного неравенства
Показательные неравенства. Решение простейшего показательного неравенства Усеченный конус
Усеченный конус