Содержание
- 2. Элементы интегрального исчисления 1.Определение определенного интеграла 2.Основные свойства определенного интеграла 3.Формула Ньютона-Лейбница 4.Методы интегрирования 5.Геометрические приложения
- 3. Определенный интеграл, его свойства и вычисление
- 4. Понятие определенного интеграла Рассмотрим функцию y=f(x), непрерывную и ограниченную на отрезке [a,b]. Разобьем [a,b] на n
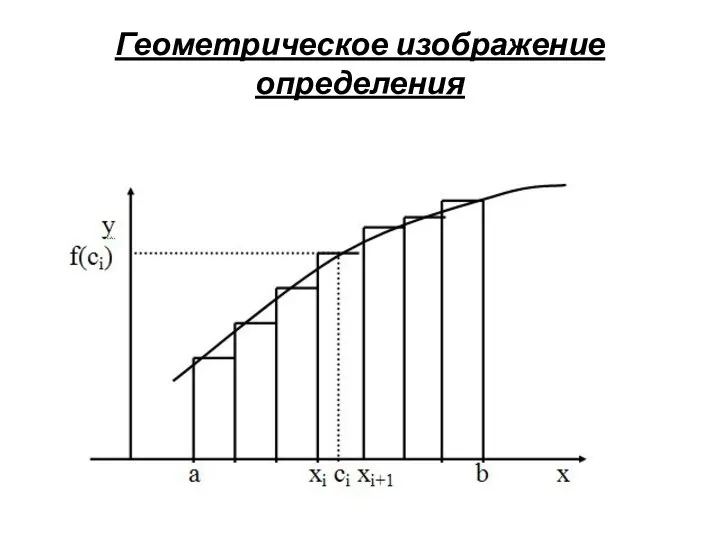
- 5. Геометрическое изображение определения
- 6. Определение интегральной суммы Интегральной суммой для функции y=f(x) на отрезке [a,b] называется сумма произведений длин элементарных
- 7. Определение определенного интеграла Определенным интегралом от функции f(x) на отрезке [a,b] называется предел (если он существует)
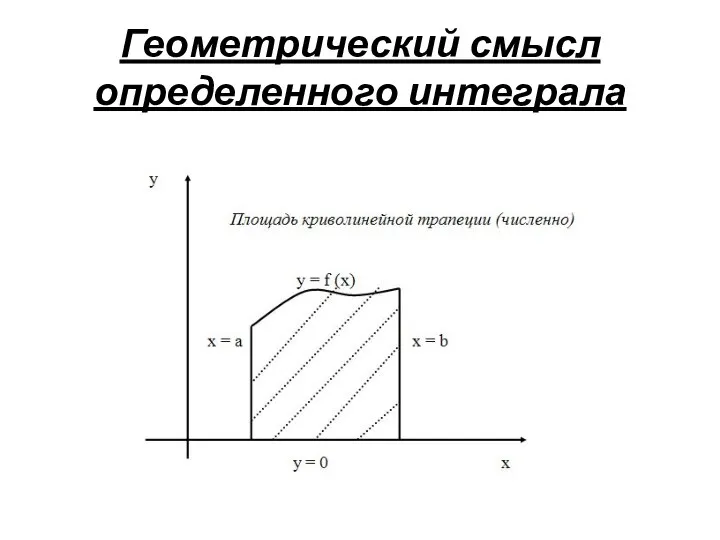
- 8. Геометрический смысл определенного интеграла
- 9. Основные свойства определенного интеграла 10 Величина определенного интеграла не зависит от обозначения переменной интегрирования (инвариантность): 20
- 10. Основные свойства определенного интеграла 30 Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то
- 11. Основные свойства определенного интеграла 40 Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой
- 12. Основные свойства определенного интеграла 50. Если подынтегральная функция f(x) на отрезке интегрирования сохраняет постоянный знак, то
- 13. Основные свойства определенного интеграла 70. Определенный интеграл от непрерывной функции равен произведению значения этой функции в
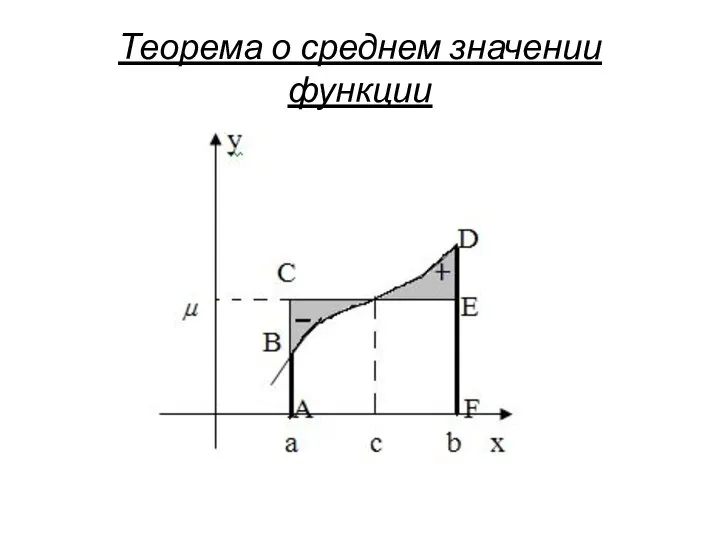
- 14. Теорема о среднем значении функции
- 15. Формула Ньютона-Лейбница. Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов интегрирования.
- 16. Методы интегрирования
- 17. Непосредственное интегрирование Этот способ основан на использовании свойств определенного интеграла, приведении подынтегрального выражения к табличной форме
- 18. Замена переменной Вычислить .
- 19. Интегрирование по частям Вычислить .
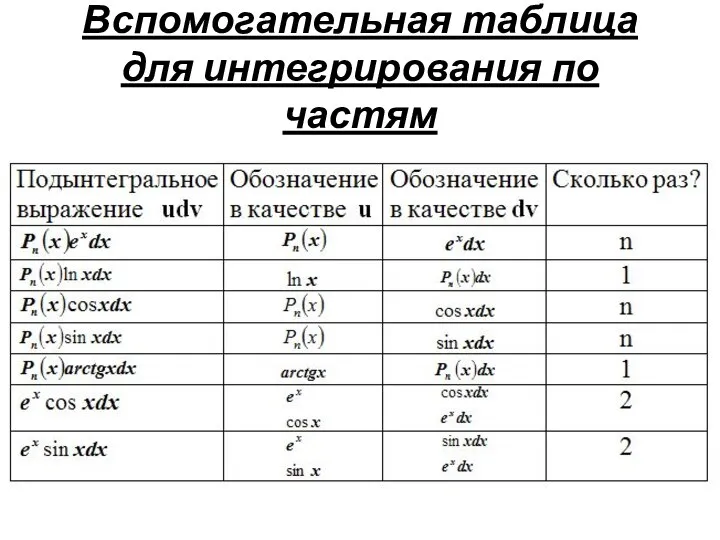
- 20. Вспомогательная таблица для интегрирования по частям
- 22. Скачать презентацию



![Определение интегральной суммы Интегральной суммой для функции y=f(x) на отрезке [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1458397/slide-5.jpg)
![Определение определенного интеграла Определенным интегралом от функции f(x) на отрезке [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1458397/slide-6.jpg)

![Основные свойства определенного интеграла 30 Если промежуток интегрирования [a,b] разбит на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1458397/slide-9.jpg)








 Презентация по математике "Подготовка к ЕГЭ Задание В8" - скачать бесплатно
Презентация по математике "Подготовка к ЕГЭ Задание В8" - скачать бесплатно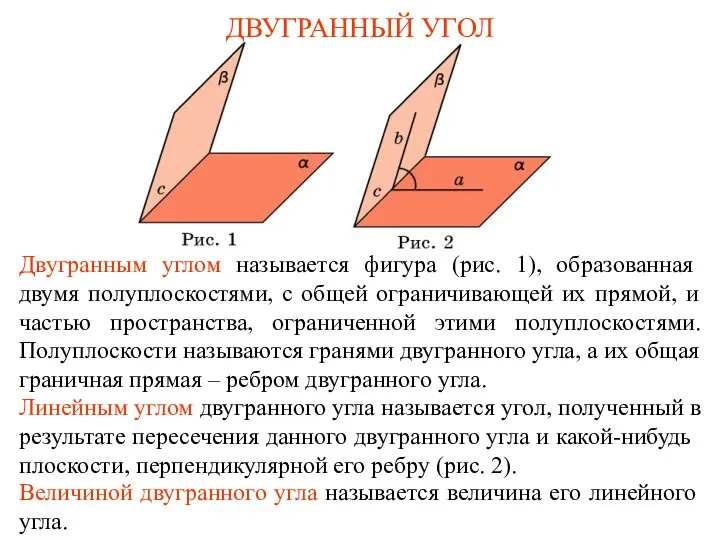 Двугранный угол. (1)
Двугранный угол. (1) Презентация на тему Неравенства и их решения
Презентация на тему Неравенства и их решения  Классификация погрешностей. Расчёт погрешностей измерений медико-биологической величины
Классификация погрешностей. Расчёт погрешностей измерений медико-биологической величины Презентация по математике "Число 5. Цифра 5 (1 класс)" - скачать
Презентация по математике "Число 5. Цифра 5 (1 класс)" - скачать  Аттестационная работа. Программа внеурочной деятельности «Реальная математика»
Аттестационная работа. Программа внеурочной деятельности «Реальная математика» Презентация по математике "Тренажёр «Квадратные корни»" - скачать
Презентация по математике "Тренажёр «Квадратные корни»" - скачать  Интеграл Определение первообразной Урок № 1
Интеграл Определение первообразной Урок № 1 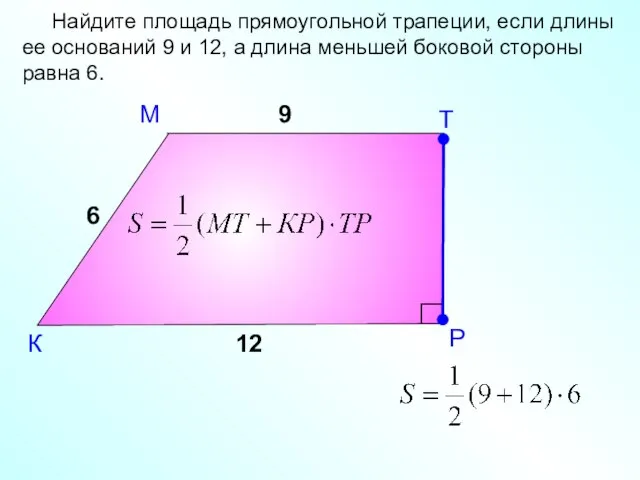 Площадь трапеции
Площадь трапеции Установите соответствие между словами
Установите соответствие между словами Канонический вид многочлена с одной переменной (урок 66)
Канонический вид многочлена с одной переменной (урок 66) Задачи военно-прикладного характера
Задачи военно-прикладного характера Графики тригонометрических функций
Графики тригонометрических функций Практикум. «Математика вокруг нас» при изучении темы «Симметрия»
Практикум. «Математика вокруг нас» при изучении темы «Симметрия» Устный счет
Устный счет Преобразование логических выражений
Преобразование логических выражений Компьютерное моделирование физических процессов, как средство формирования математических понятий
Компьютерное моделирование физических процессов, как средство формирования математических понятий Письменное вычитание с переходом через десяток
Письменное вычитание с переходом через десяток Десятичная запись дробных чисел
Десятичная запись дробных чисел Угол между прямой и плоскостью (решение задач)
Угол между прямой и плоскостью (решение задач) Длина окружности
Длина окружности Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Комплексный экзамен. Математика
Комплексный экзамен. Математика Показательные уравнения
Показательные уравнения Основное свойство дроби
Основное свойство дроби Сложение с переходом через десяток вида + 7
Сложение с переходом через десяток вида + 7 Урок-проект во 2 классе Тема: «Наша страничка в учебнике математики». Работу выполнила Дерябина Наталья Викторовна, учитель началь
Урок-проект во 2 классе Тема: «Наша страничка в учебнике математики». Работу выполнила Дерябина Наталья Викторовна, учитель началь Аттестационная работа. Элективный курс по математике «Избранные вопросы математики». (8 класс)
Аттестационная работа. Элективный курс по математике «Избранные вопросы математики». (8 класс)