Содержание
- 2. а) Рівняння, що не містить шукану функцію у Рівняння (1) явно не містить шукану функцію у.
- 3. загальний розв’язок: . Тоді загальний інтеграл буде мати вигляд: б) Рівняння, що не містить незалежну змінну
- 4. Підставимо знайдені вирази у рівняння (2) і отримаємо: . Звідси знайдемо: . Тоді . Проінтегрувавши останнє
- 5. 2. Лінійні однорідні диференціальні рівняння. Означення. Диференціальне рівняння другого порядку наз. лінійним, якщо шукана функція у
- 6. Теорема 1. Якщо -2 частинних розв’язки лінійного однорідного диференціального рівняння 2 порядку: то -також є розв’язком
- 7. Означення. Розв’язки лінійного однорідного диференціального рівняння 2 порядку лінійно незалежні на : якщо . Теорема 3.
- 8. Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами. Лінійне однорідне диференціальне рівняння другого порядку зі
- 9. Рівняння (5) наз. характеристичним рівнянням для рівняння (4). Характеристичне рівняння- це квадратне рівняння, що має 2
- 10. У випадку: , де: Корені комплексно спряжені. Загальний розв’язок рівняння (4) має вигляд:
- 11. 3.Неоднорідні лінійні рівняння другого порядку зі сталими коефіцієнтами . Розглянемо неоднорідне лінійне диференціальне рівняння другого порядку:
- 12. Розглянемо неоднорідне лінійне диференціальне рівняння другого порядку зі сталими коефіцієнтами: (8) Якщо , то рівняння (9)
- 13. Розглянемо декілька випадків. Нехай права частина рівняння (8) є добуток показникової функції на поліном n-того степеня,
- 14. Підставивши вираз для у рівняння (8), скоротивши на і прирівнявши коефіцієнти при однакових степенях х, отримаємо
- 16. Скачать презентацию













 Что такое математика?
Что такое математика? Линейные дискретные системы. Введение
Линейные дискретные системы. Введение Как построить график функции y=f(x+l)+m, если известен график функции y=f(x). 8 класс
Как построить график функции y=f(x+l)+m, если известен график функции y=f(x). 8 класс Количественный счет
Количественный счет Средние величины. (Лекция 4.2)
Средние величины. (Лекция 4.2)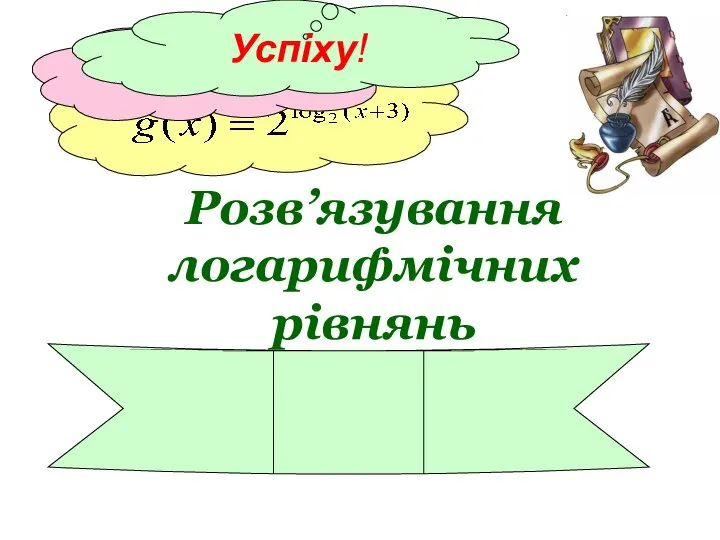 Розв’язування логарифмічних рівнянь
Розв’язування логарифмічних рівнянь Квадрат и куб
Квадрат и куб формулы сокращенного умножения. Георг Кристоф Лихтенберг (1742 - 1799)
формулы сокращенного умножения. Георг Кристоф Лихтенберг (1742 - 1799) Геометрические фигуры
Геометрические фигуры Правильные многоугольники. Геометрия 9 класс
Правильные многоугольники. Геометрия 9 класс Способы решения комбинаторных задач
Способы решения комбинаторных задач Показательная функция, её свойства и график
Показательная функция, её свойства и график Методы преобразования эпюра
Методы преобразования эпюра Занимательная математика
Занимательная математика Предел и непрерывность функции
Предел и непрерывность функции Математические задачи от русских, советских и зарубежных писателей МОУ «Средняя общеобразовательная школа №42 с углубленным из
Математические задачи от русских, советских и зарубежных писателей МОУ «Средняя общеобразовательная школа №42 с углубленным из Арифметическая прогрессия
Арифметическая прогрессия Значение логико-математических игр в умственном и речевом развитии детей старшего дошкольного возраста
Значение логико-математических игр в умственном и речевом развитии детей старшего дошкольного возраста Вписанные окружности (решение задач)
Вписанные окружности (решение задач) Турнир эрудитов. 9 - 11 классы
Турнир эрудитов. 9 - 11 классы Элементы комбинаторики.
Элементы комбинаторики. Математическая модель. 5 класс
Математическая модель. 5 класс Работа выполнена: Ученицей 10 класса «б» МБОУСОШ №1 г. Новочеркасска Пасенчук Анастасией под руководством учителя
Работа выполнена: Ученицей 10 класса «б» МБОУСОШ №1 г. Новочеркасска Пасенчук Анастасией под руководством учителя  Информационный проект Бюджет семьи Исполнители: ученицы 10 класса МКОУ « Горбуновская СОШ», Денисова Ири
Информационный проект Бюджет семьи Исполнители: ученицы 10 класса МКОУ « Горбуновская СОШ», Денисова Ири Аттестационная работа. Образовательная программа элективного курса Тайны квадратного трехчлена
Аттестационная работа. Образовательная программа элективного курса Тайны квадратного трехчлена Косинус угла
Косинус угла Вводное повторение. 7 класс
Вводное повторение. 7 класс Тема урока: Простые и составные числа. Презентацию подготовила Учитель математики МОУ ООШ с.Студёновка Гончарова Ольга Евге
Тема урока: Простые и составные числа. Презентацию подготовила Учитель математики МОУ ООШ с.Студёновка Гончарова Ольга Евге