Дифференциальные уравнения

Тема 1. Дифференциальные уравнения первого порядка
§1. Основные понятия
§2. Теорема существования и единственности

§1. Основные понятия

ОПРЕДЕЛЕНИЕ. Обыкновенным дифференциальным уравнением (ОДУ) называется уравнение, связывающее независимую

Замечание. Уравнение, связывающее неизвестную функцию
n переменных, ее аргументы и ее

График решения (интеграла) дифференциального уравнения называется интегральной кривой.
Процесс нахождения решений дифференциального

§2. Теорема существования и единственности
решения задачи Коши для уравнения y ′ = f(x,y)
Общий вид

ТЕОРЕМА 1 (Коши).
Пусть для уравнения y ′ = f(x,y) выполняются два условия:
1) f(x,y)

Задача нахождения решения дифференциального уравнения F(x,y,y ′)=0, удовлетворяющего начальному условию y(x0) = y0, называется

Замечание. Теорема 1 дает достаточные условия существо- вания и единственности решения задачи

ОПРЕДЕЛЕНИЕ. Общим решением дифференциального урав- нения y ′ = f(x,y) в области D существования и единствен- ности

Любое решение (интеграл), получающееся из общего решения (интеграла) при конкретном значении

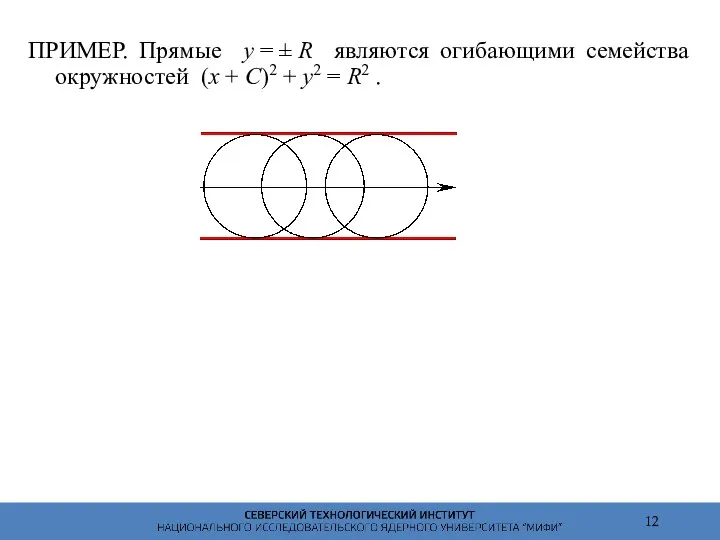
ПРИМЕР. Прямые y = ± R являются огибающими семейства окружностей (x + C)2 + y2 = R2 .

§3. Уравнения с разделенными переменными

ДУ 1-го порядка, разрешенное относительно y ′,

Пусть F(x) – первообразная функции f(x),
Φ(y) – первообразная функции ϕ(y).

§4. Уравнения с разделяющимися переменными

Дифференциальным уравнением с разделяющимися
переменными называется

Замечания.
1) Деление на ϕ1(y) ⋅ f2(x) может привести к потере решений. Поэтому

§5. Однородные уравнения

Функция M(x , y) называется однородной степени m (или изме- рения

Дифференциальное уравнение первого порядка
y ′ = f(x , y)
называется однородным относительно x и y, если функция

§6. Уравнения, приводящиеся к однородным

1. Уравнения вида
Рассмотрим уравнение (7)
Если c1 = c2 = 0 , то

Это зависит от определителя
а) Если Δ ≠ 0 , то (7) приводится к однородному

б) Если Δ = 0  , то уравнение (7) приводится к уравнению с разделяющимися

2. Обобщенно однородные уравнения

Уравнение 1-го порядка называется обобщённо однородным, если

§7. Линейные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка называется

Линейное однородное уравнение
y ′ + p(x) ⋅ y = 0
является уравнением с разделяющимися переменными.
Его общее решение:
(9)
Рассмотрим линейное

2) Полагаем, что решение неоднородного уравнения по структуре совпадает с решением соответствующего линей- ного

Замечания.
1) Раскроем скобки в (10):
(11)
Заметим, что первое слагаемое в (11)

II) Метод Бернулли.
Будем искать решение (8) в следующем виде:
y = u(x) ⋅ v(x) .
Тогда y ′ = u ′ ⋅ v + u ⋅ v ′ .
Подставим

Условия (12) позволяют однозначно определить v(x) и u(x) .
При этом получим
Замечание.

§8. Уравнения Бернулли

Уравнением Бернулли называется уравнение вида
y ′ + p(x) ⋅ y = f(x) ⋅ y n , (13)
где p(x) ,  f(x) –

2) Решив получившееся после замены линейное уравнение методом Бернулли, получим:
z = u(x) ⋅ v(x) ,
Таким образом, решение

§9. Уравнения в полных дифференциалах

Уравнение M(x , y)dx + N(x , y)dy = 0  (14)
называется уравнением в полных дифференциалах, если

ТЕОРЕМА 2.
Пусть функции M(x , y) , N(x , y) определены и непрерывны в области

Способы нахождения функции u(x , y):
1) используя алгоритм, предложенный в доказательстве теоре- мы 2;
2)

3) методом интегрируемых комбинаций.
Суть метода интегрируемых комбинаций: выделить в
M(x , y)dx + N(x , y)dy
выражения,

§10. Интегрирующий множитель

Функция μ(x,y) называется интегрирующим множителем уравнения M(x , y)dx + N(x , y)dy = 0, (14)
если