Два треугольника подобны, если их углы соответственно равны и сходственные стороны
пропорциональны.
Два равносторонних треугольника всегда подобны.
Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
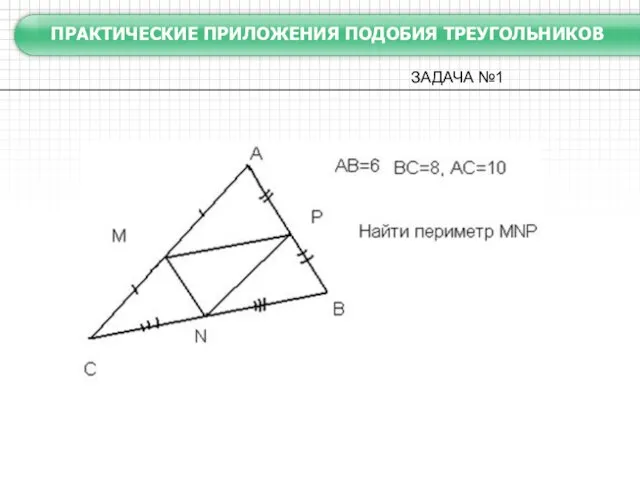
Стороны одного треугольника имеют длины 3, 4, 6 см, стороны другого треугольника равны 9, 14, 18 см. Подобны ли эти треугольники?
Периметры подобных треугольников относятся как квадраты сходственных сторон.
Если два угла одного треугольника равны 60° и 50° , а два угла другого треугольника равны 50° и 80°, то такие треугольники подобны.
Два прямоугольных треугольника подобны, если имеют по равному острому углу.
Два равнобедренных треугольника подобны, если их боковые стороны пропорциональны.
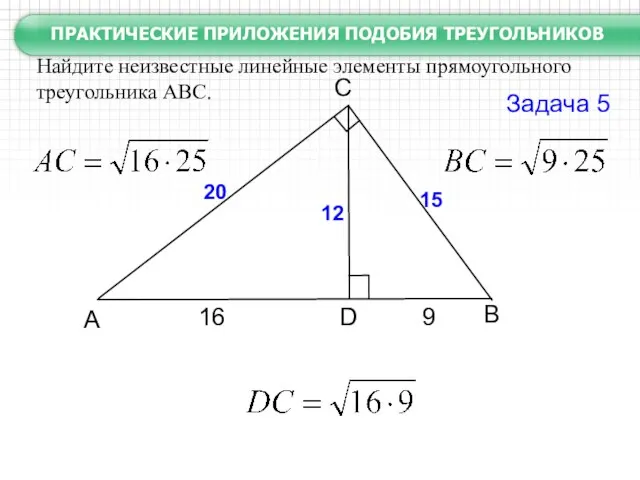
Если отрезки гипотенузы, на которые она делится высотой, проведенной из вершины прямого угла, равны 2 и 8 см, то эта высота равна 4 см.
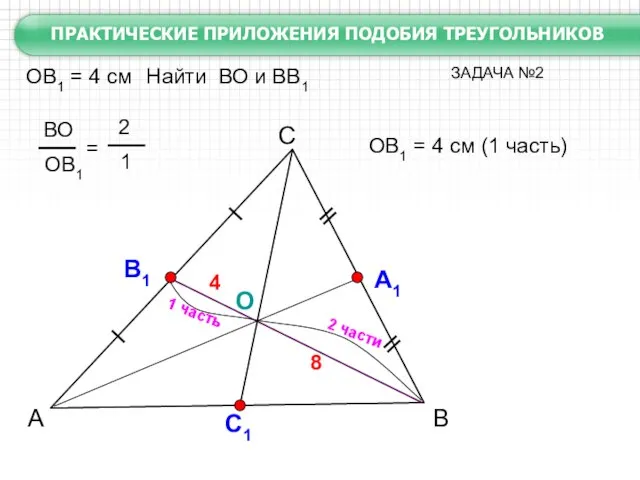
Если медиана треугольника равна 9 см, то расстояние от вершины треугольника до точки пересечения медиан равно 6 см.
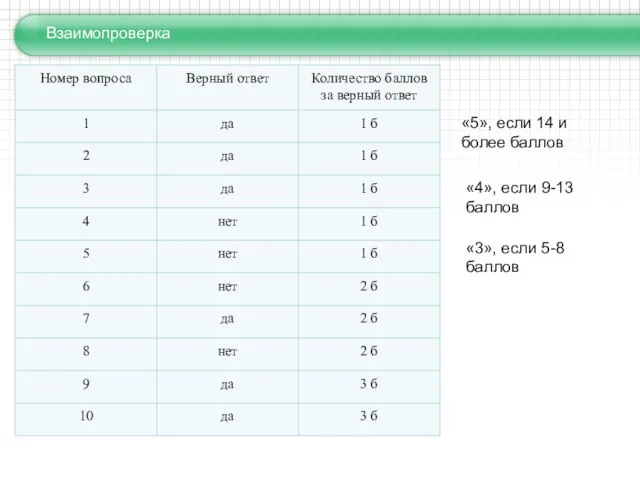
Тест Если высказывание истинно – отвечаем “Да”, если ложно – “Нет”







 Понятие логарифма
Понятие логарифма Математические фокусы
Математические фокусы Конус
Конус II городской турнир по ментальной арифметике
II городской турнир по ментальной арифметике Многогранники в нашей жизни
Многогранники в нашей жизни История возникновения геометрии
История возникновения геометрии Математический турнир
Математический турнир Признаки делимости на 2; 3; 5; 9; 10
Признаки делимости на 2; 3; 5; 9; 10 Функция y=sinx
Функция y=sinx Положительные и отрицательные числа. 6 класс
Положительные и отрицательные числа. 6 класс Итоговый тест по математике. 2 класс. УМК «Гармония»
Итоговый тест по математике. 2 класс. УМК «Гармония» Графики. График движения
Графики. График движения Статистическая теория радиотехнических систем. Моменты случайных функций. (Лекция 3)
Статистическая теория радиотехнических систем. Моменты случайных функций. (Лекция 3) Остапенко Ирина Борисовна, Учитель математики и информатики, МОУ Барановская СОШ 2011 г.
Остапенко Ирина Борисовна, Учитель математики и информатики, МОУ Барановская СОШ 2011 г. Решение уравнений и неравенств, содержащих переменную под знаком модуля
Решение уравнений и неравенств, содержащих переменную под знаком модуля Математические открытия
Математические открытия Математика
Математика Площадь параллелограмма
Площадь параллелограмма Четырехугольники 8 класс
Четырехугольники 8 класс Параллельные прямые
Параллельные прямые Графы и их применение к решению задач
Графы и их применение к решению задач Десятичные дроби
Десятичные дроби Проценты. Урок математики в 5 классе
Проценты. Урок математики в 5 классе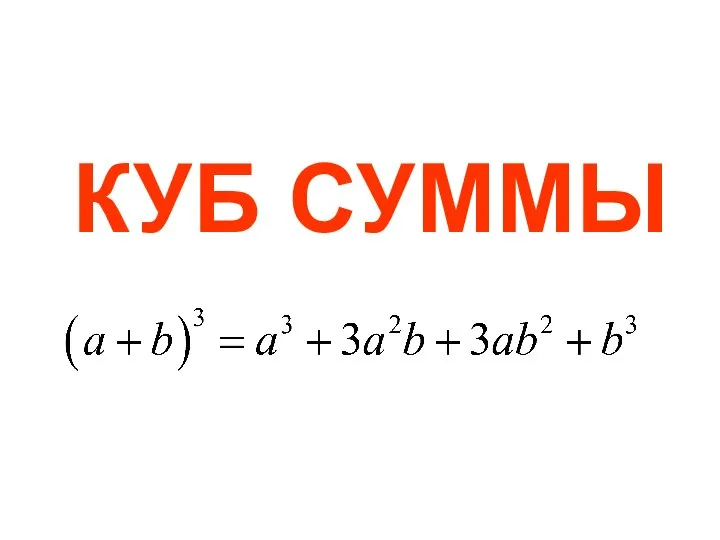 Куб суммы
Куб суммы Квадратные уравнения. Методическая разработка раздела программы по алгебре 8 класса
Квадратные уравнения. Методическая разработка раздела программы по алгебре 8 класса Тайны чисел. Фигурные числа
Тайны чисел. Фигурные числа Методы построения математических моделей на основе активного эксперимента
Методы построения математических моделей на основе активного эксперимента Аттестационная работа. Математическое общество учащихся «Ориентир»
Аттестационная работа. Математическое общество учащихся «Ориентир»