Содержание
- 2. Рекомендуемая литература Баврин И.И. Дискретная математика: учебник и задачник для прикладного бакалавриата.- М.: Издательство Юрайт, 2015.-
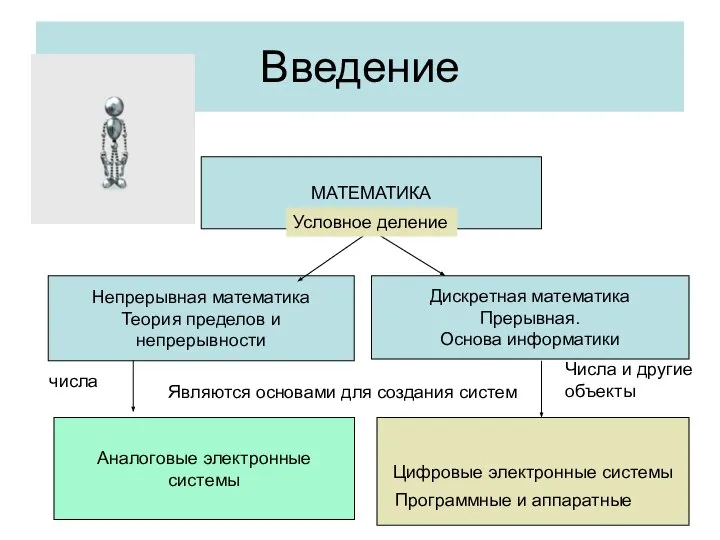
- 3. Введение МАТЕМАТИКА Непрерывная математика Теория пределов и непрерывности Дискретная математика Прерывная. Основа информатики Являются основами для
- 4. Разделы дискретной математики Теория множеств. Комбинаторика Теория графов. Алгебра логики. Матрицы. Разностные уравнения. Дискретная вероятность.
- 5. Задачи курса УМЕТЬ Правильно употреблять математическую символику и оперировать математическим инструментарием. Классифицировать задачу. Выбирать модель представления
- 6. Раздел 1. Элементы теории 1.1 Множества и операции над ними Множество – это совокупность, собрание каких-либо
- 7. Примеры Учебник –страницы. Группа ВТ-115 – ФИО студентов. Серия микросхем – состав серии.
- 8. Обозначения числовых множеств N – множество натуральных чисел; N0 – множество неотрицательных целых чисел; Z –
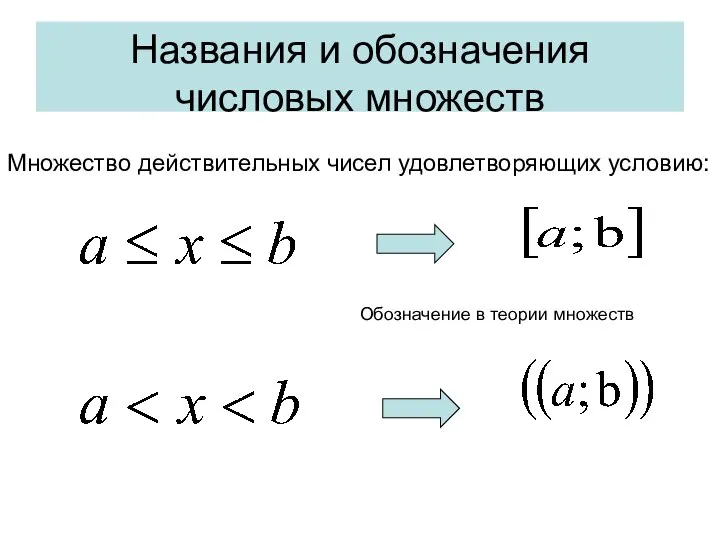
- 9. Названия и обозначения числовых множеств Множество действительных чисел удовлетворяющих условию: Обозначение в теории множеств
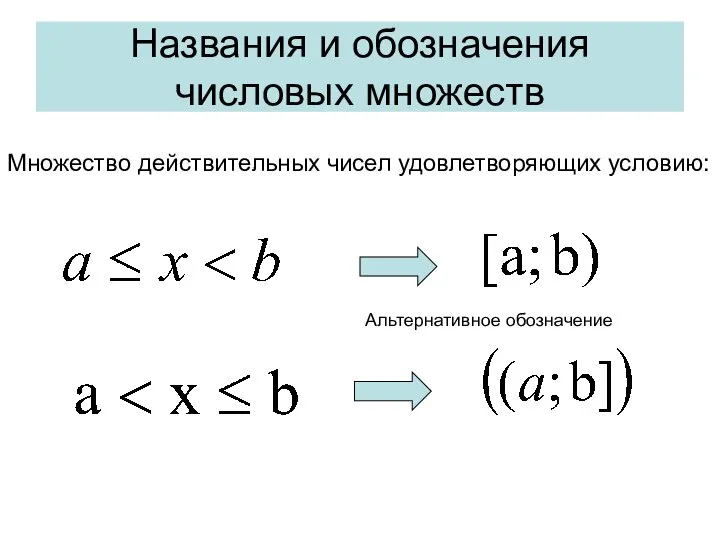
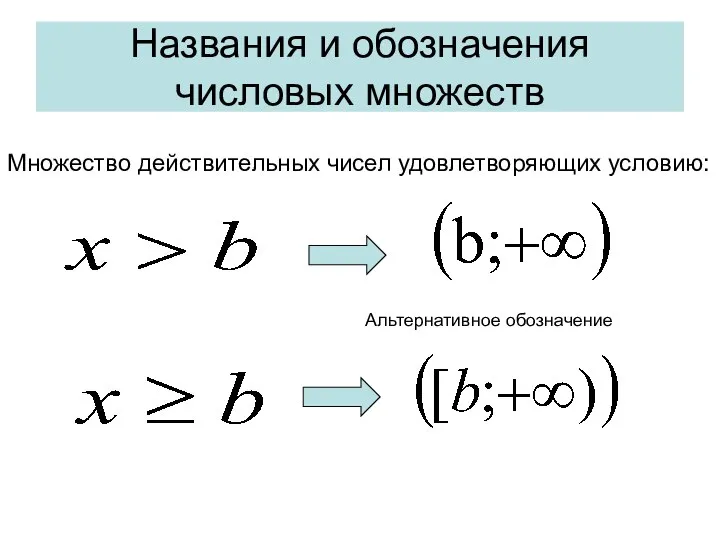
- 10. Названия и обозначения числовых множеств Множество действительных чисел удовлетворяющих условию: Альтернативное обозначение
- 11. Названия и обозначения числовых множеств Множество действительных чисел удовлетворяющих условию: Альтернативное обозначение
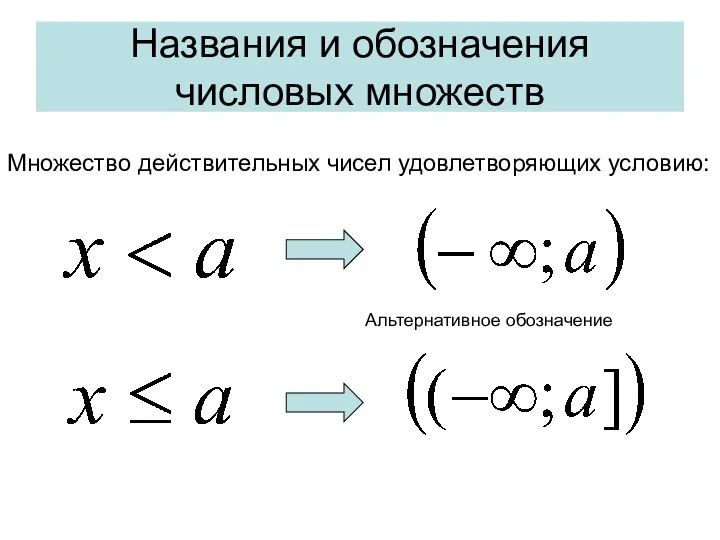
- 12. Названия и обозначения числовых множеств Множество действительных чисел удовлетворяющих условию: Альтернативное обозначение
- 13. Названия и обозначения числовых множеств Множество всех действительных чисел обозначается: ИЛИ ИЛИ R Множество всех положительных
- 14. Множества конечные и бесконечные Множество содержащее конечное число элементов называют конечным, в противоположном случае множество называю
- 15. Формы задания множества 1 способ Например: А = {1,2,3} – означает, что множество А состоит из
- 16. Формы задания множества 2 способ Заключается в описании элементов определяющим свойством P (x), общим для всех
- 17. C = {x: x – пациент больницы №4 г.Владимир} D = {x: x – студент группы
- 18. Порождающая процедура описывает способ получения элементов множества из других объектов или уже полученных элементов множества. Формы
- 19. Равенство множеств Если множество А и множество В состоит из одних и тех же элементов, то
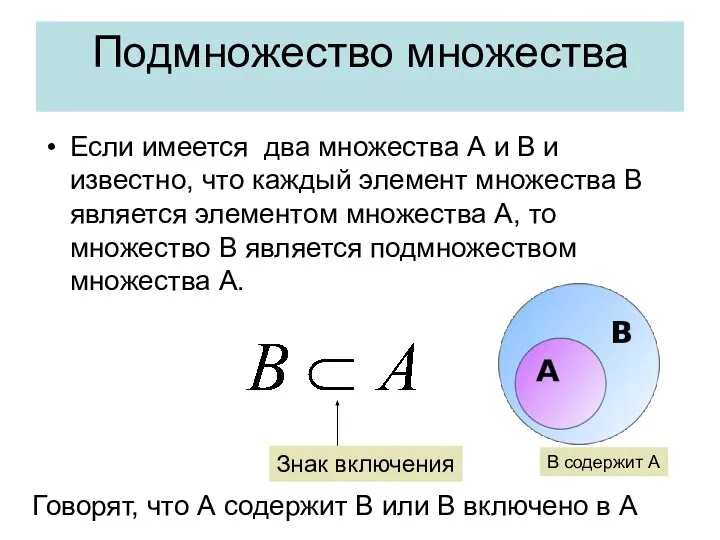
- 20. Подмножество множества Если имеется два множества А и В и известно, что каждый элемент множества В
- 21. Пример 1: Множество четных чисел, есть подмножество множества целых чисел. Пример 2: А={x: x – группа
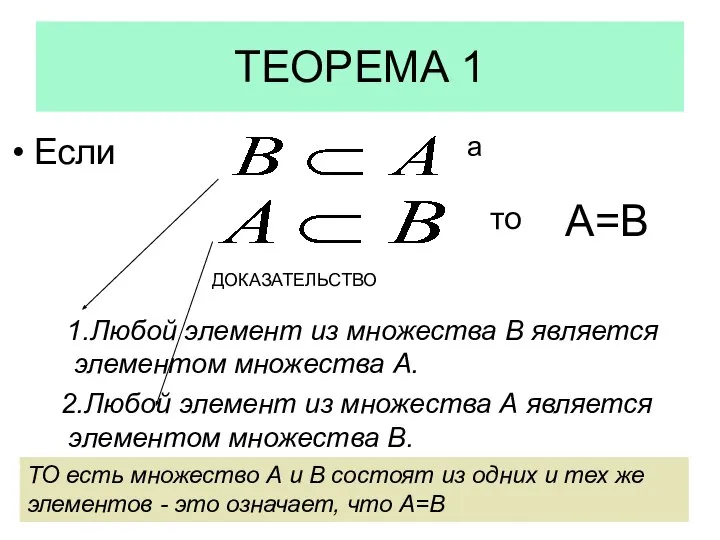
- 22. ТЕОРЕМА 1 Если а то А=В 1.Любой элемент из множества В является элементом множества А. 2.Любой
- 23. Определение - булеан Элементами множества могут быть подмножества. Множество всех подмножеств множества А называется его булеаном
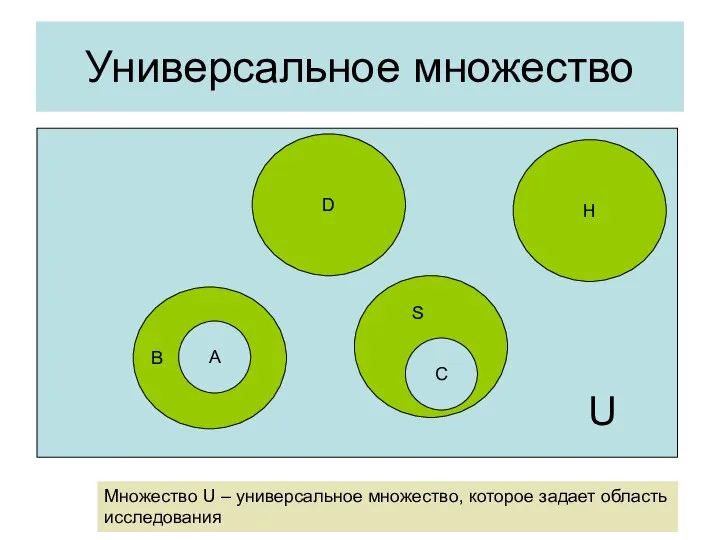
- 24. Универсальное множество D H A C B S U Множество U – универсальное множество, которое задает
- 25. Пустое множество Множество, не содержащее ни одного элемента называется пустым и обозначается знаком: Пример1: множество людей
- 26. ТЕОРЕМА 2 Пустое множество является подмножеством любого множества. ДОКАЗАТЕЛЬСТВО Из определения подмножества следует, что В является
- 27. Операции над множествами Объединение или сумма ОПРЕДЕЛЕНИЕ: если даны два множества А и В, то их
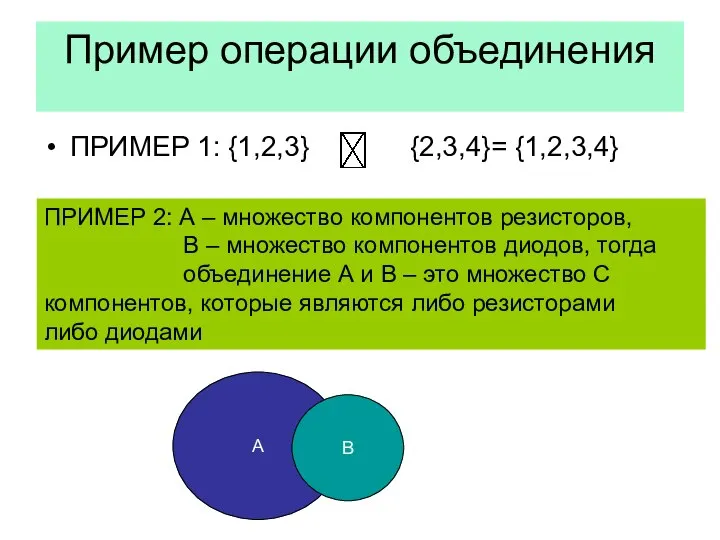
- 28. Пример операции объединения ПРИМЕР 1: {1,2,3} {2,3,4}= {1,2,3,4} ПРИМЕР 2: А – множество компонентов резисторов, В
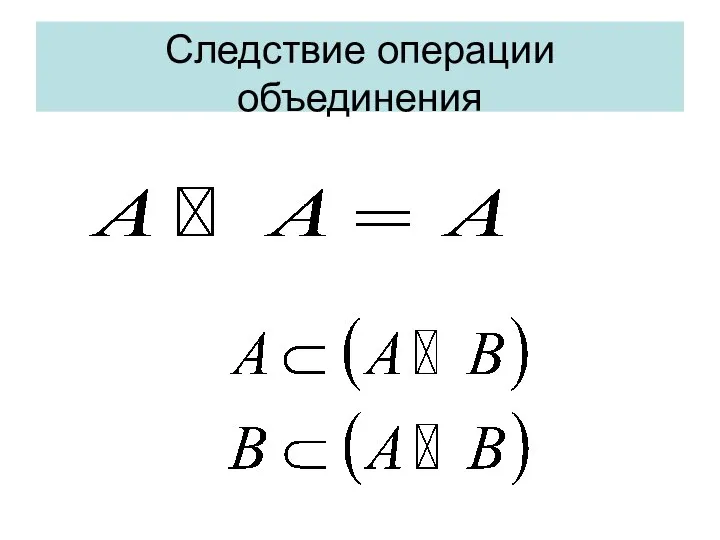
- 29. Следствие операции объединения
- 30. Объединение N множеств Операция объединения может быть распространена на N множеств. Тогда записывают:
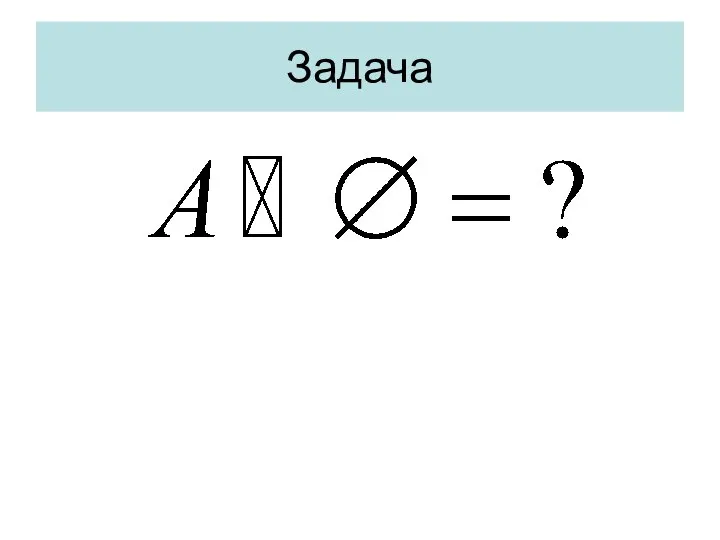
- 31. Задача
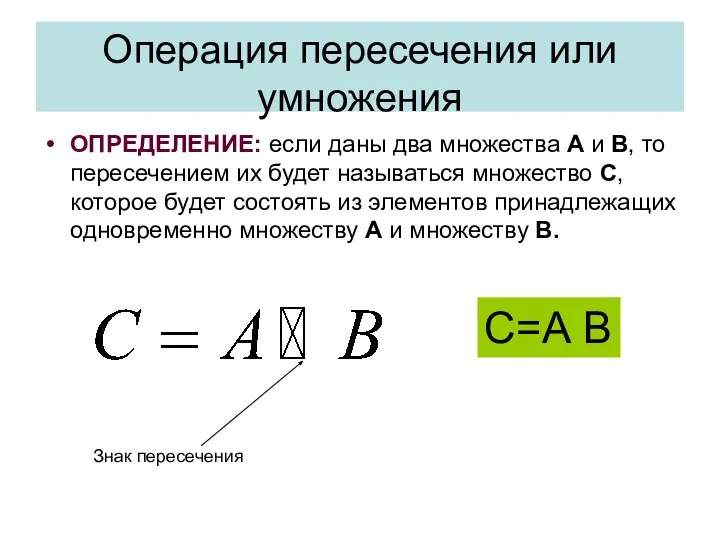
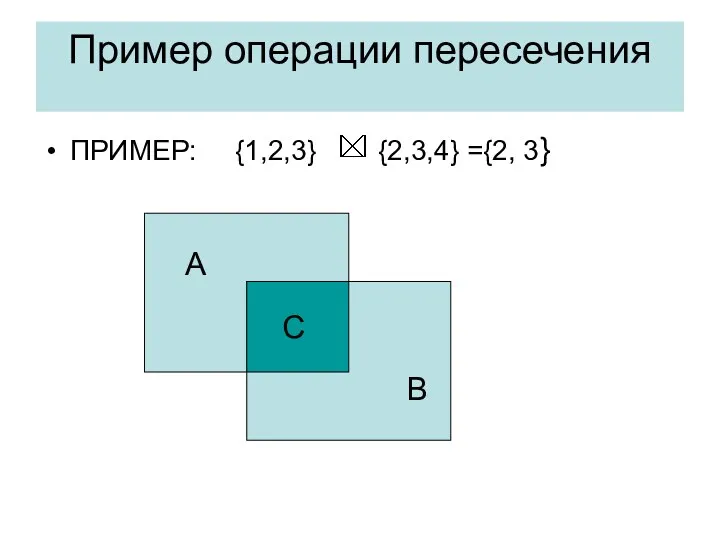
- 32. Операция пересечения или умножения ОПРЕДЕЛЕНИЕ: если даны два множества А и В, то пересечением их будет
- 33. Пример операции пересечения ПРИМЕР: {1,2,3} {2,3,4} ={2, 3} А В С
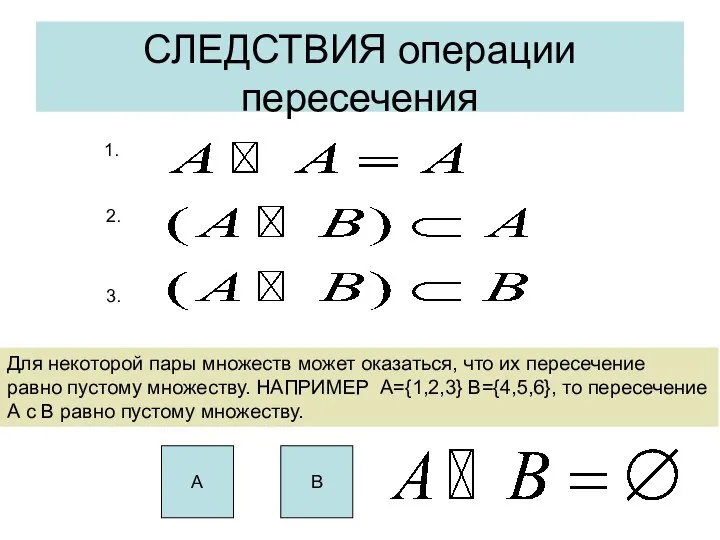
- 34. СЛЕДСТВИЯ операции пересечения Для некоторой пары множеств может оказаться, что их пересечение равно пустому множеству. НАПРИМЕР
- 35. Непересекающиеся множества Множества, пересечение которых, является пустым множеством называются непересекающимися. ПРИМЕР 1: А – множество целых
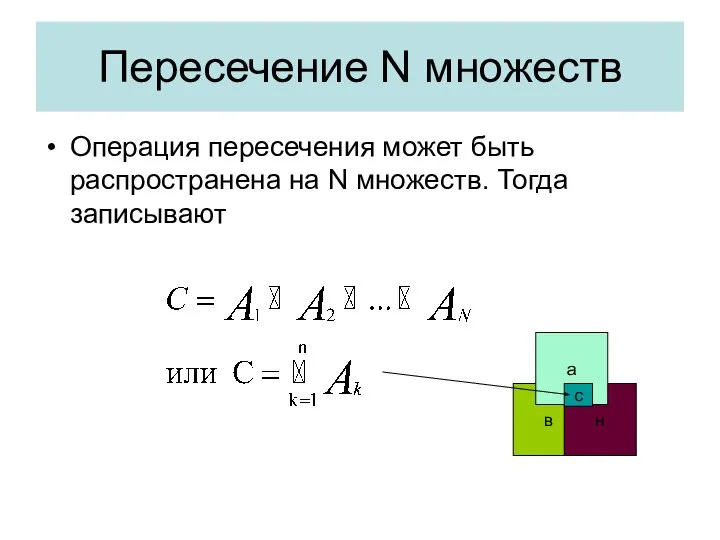
- 36. Пересечение N множеств Операция пересечения может быть распространена на N множеств. Тогда записывают в н а
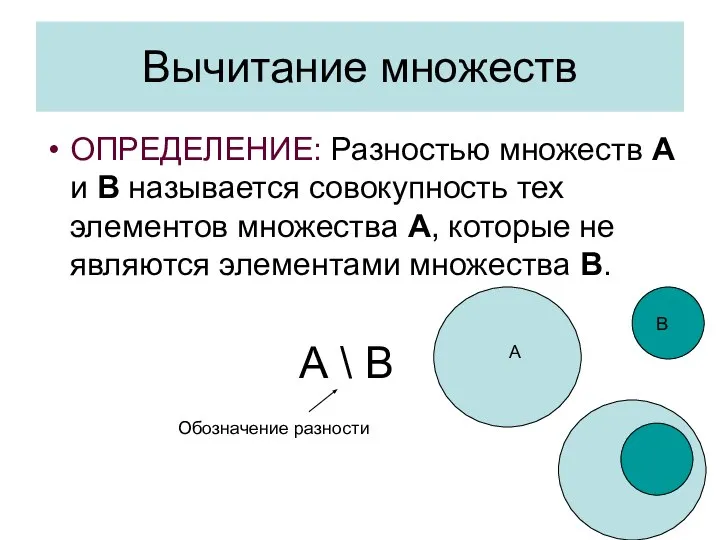
- 37. Вычитание множеств ОПРЕДЕЛЕНИЕ: Разностью множеств А и В называется совокупность тех элементов множества А, которые не
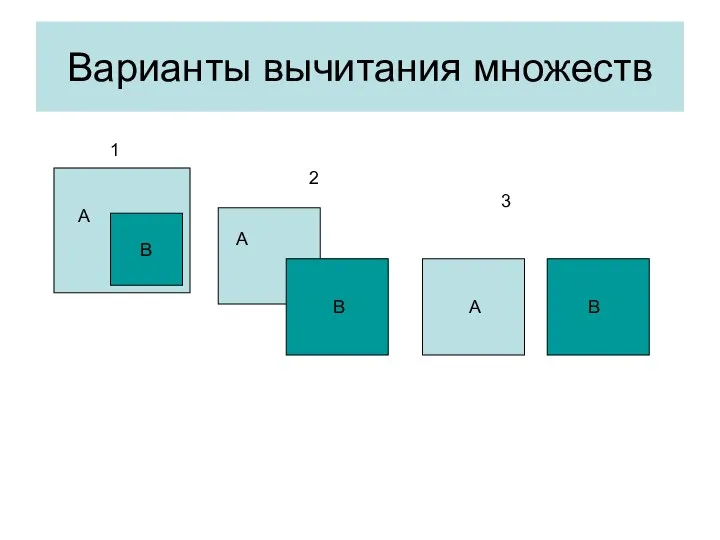
- 38. Варианты вычитания множеств А В А В А В 1 2 3
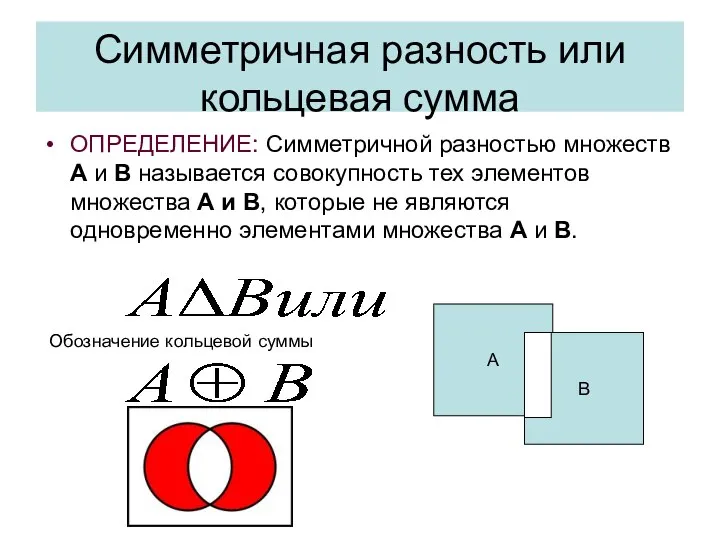
- 39. Симметричная разность или кольцевая сумма ОПРЕДЕЛЕНИЕ: Симметричной разностью множеств А и В называется совокупность тех элементов
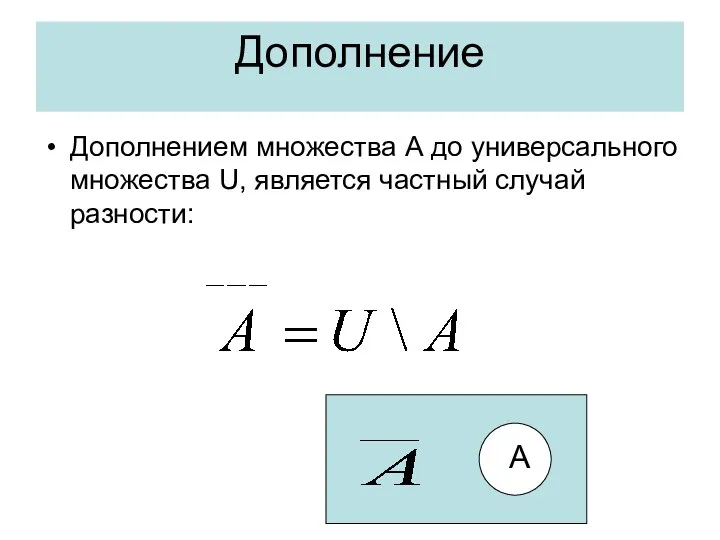
- 40. Дополнение Дополнением множества А до универсального множества U, является частный случай разности: A
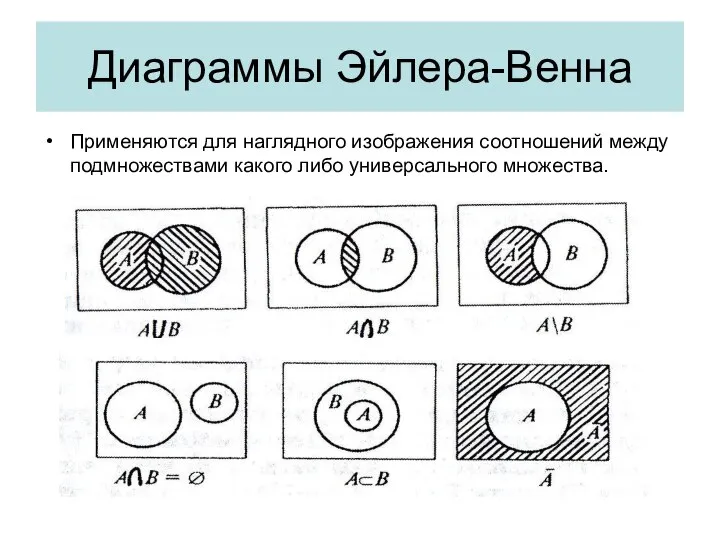
- 41. Диаграммы Эйлера-Венна Применяются для наглядного изображения соотношений между подмножествами какого либо универсального множества.
- 42. Декартово произведение множества А на множество В ОПРЕДЕЛЕНИЕ: это множество всех упорядоченных пар элементов из А
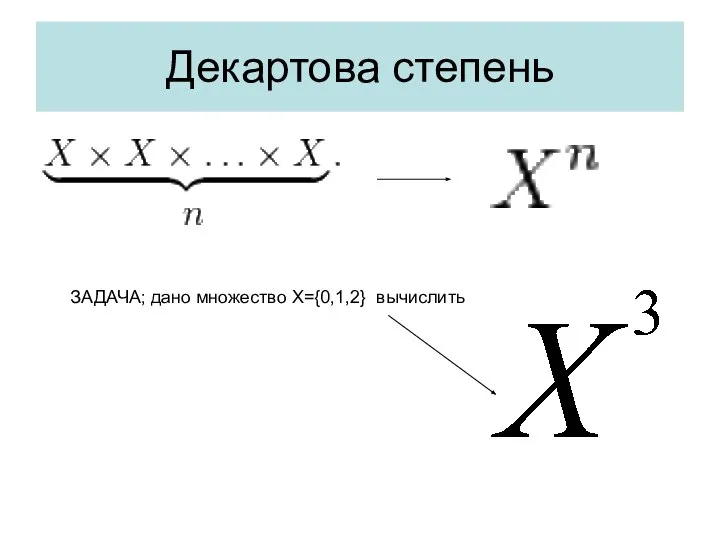
- 43. Декартова степень ЗАДАЧА; дано множество X={0,1,2} вычислить
- 44. Порядок выполнения операций над множествами Дополнение – (пересечение- объединение) и разность - умножение. Изменить порядок выполнения
- 45. Мощность множества Это характеристика количества элементов множества. Используется как класс эквивалентности над множествами, между которыми можно
- 46. Законы алгебры множеств или алгебра Буля 1. ЗАКОН. Свойство двойного дополнения. Двойное дополнение множества А равно
- 47. Законы алгебры множеств или алгебра Буля 2 ЗАКОН. Свойство идемпотентности объединения или пересечения множества А.
- 48. Законы алгебры множеств или алгебра Буля 3 ЗАКОН. Дополнения.
- 49. Законы алгебры множеств или алгебра Буля 4. ЗАКОН. Свойство единицы.
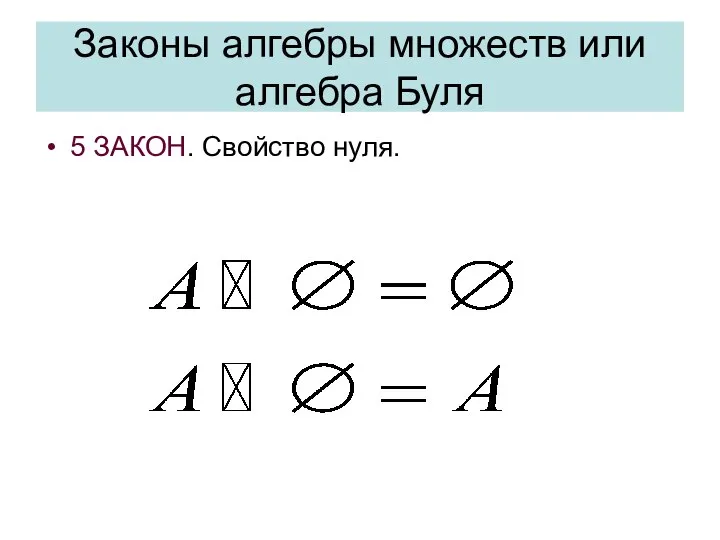
- 50. Законы алгебры множеств или алгебра Буля 5 ЗАКОН. Свойство нуля.
- 51. Законы алгебры множеств или алгебра Буля 6 ЗАКОН. де Моргана.
- 52. Законы алгебры множеств или алгебра Буля 7 ЗАКОН. Коммутативность пересечения или объединения множеств.
- 53. Законы алгебры множеств или алгебра Буля 8 ЗАКОН. Ассоциативности пересечения или объединения.
- 54. Законы алгебры множеств или алгебра Буля 9 ЗАКОН. Дистрибутивность объединения относительно пересечения и пересечения относительно объединения
- 55. Проверка закона де Моргана Пусть
- 57. Скачать презентацию
































 Методы оптимизации объектов
Методы оптимизации объектов Старинные меры длины наших предков
Старинные меры длины наших предков Квадратные уравнения
Квадратные уравнения Логарифмические неравенства
Логарифмические неравенства Сравнение многозначных чисел
Сравнение многозначных чисел Своя игра. Степень с натуральным показателем
Своя игра. Степень с натуральным показателем Векторная алгебра
Векторная алгебра Производная и ее геометрический смысл Урок обобщения и систематизации знаний
Производная и ее геометрический смысл Урок обобщения и систематизации знаний Чтение графика функций
Чтение графика функций Төртбұрыштар
Төртбұрыштар Деление на десятичную дробь
Деление на десятичную дробь Умножение и деление дробей
Умножение и деление дробей Прямоугольный параллелепипед
Прямоугольный параллелепипед Интеграл. Математика - гимнастика ума
Интеграл. Математика - гимнастика ума Решение задач на нахождение расстояний и углов в пространстве с помощью метода координат. Задание С2
Решение задач на нахождение расстояний и углов в пространстве с помощью метода координат. Задание С2 История развития математики
История развития математики Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Открытый урок по математике в 6 классе
Открытый урок по математике в 6 классе Уравнение прямой на плоскости
Уравнение прямой на плоскости Задачи с применением подобия треугольников. 8 класс
Задачи с применением подобия треугольников. 8 класс Игра-тренажер 1 класс. Состав чисел 14 – 18
Игра-тренажер 1 класс. Состав чисел 14 – 18 Обобщение и углубление знаний о круглых телах
Обобщение и углубление знаний о круглых телах Сложение и вычитание натуральных чисел
Сложение и вычитание натуральных чисел Материалы к урокам геометрии в 8 классе по теме: «Подобие треугольников. Признаки подобия треугольников»
Материалы к урокам геометрии в 8 классе по теме: «Подобие треугольников. Признаки подобия треугольников» Случайные величины (Лекция 8)
Случайные величины (Лекция 8) Численные методы решения уравнений
Численные методы решения уравнений Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Задачі timss. (8 клас)
Задачі timss. (8 клас)