Содержание
- 2. Определение: Неравенства, содержащие переменную под знаком логарифма, называются логарифмическими. Например:
- 3. I. Типы простейших логарифмических неравенств или называются простейшими логарифмическими неравенствами Неравенства вида или Неравенства можно переписать
- 4. Решение логарифмических неравенств основано на свойстве монотонности функции y = logat : при a > 1
- 5. Методы решения логарифмических неравенств. І) Неравенство вида logaf(x) > c (или logaf(x) > c, logaf(x) >
- 6. Пример. Решить неравенство log7(4x + 1) ≥ 2 Решение. log7(4x + 1) ≥ log749 4x +
- 7. 2) Если 0 убывает на R+ и неравенство logaf(x) > c равносильно системе Систему в этом
- 8. Пример. Решить неравенство log1/2(1 – x) > 2 Решение. log1/2(1 – x) > log1/2(1/4) 3/4 Ответ:
- 9. І І. Неравенство вида logaf(x) > logaφ(x) или logaf (x) 1) Если a > 1, то
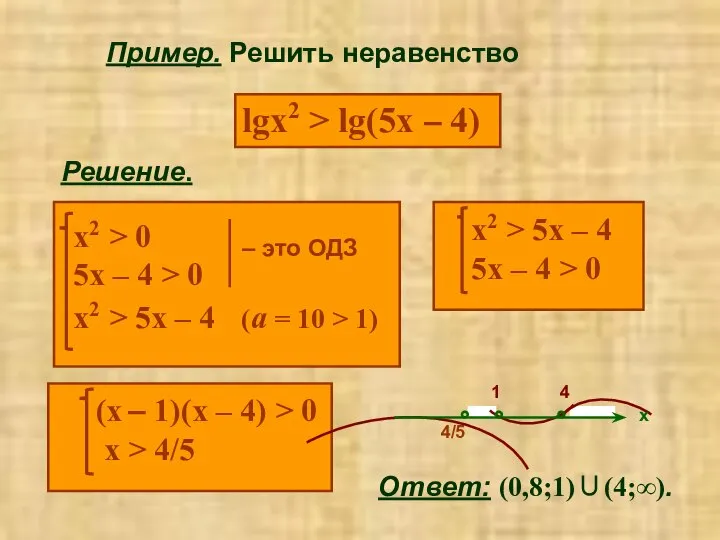
- 10. Пример. Решить неравенство lgx2 > lg(5x – 4) Решение. Ответ: (0,8;1)∪(4;∞).
- 11. 2) Если 0 убывает на R+ и неравенство logaf(x) > logaφ(x) равносильно системе І І. Неравенство
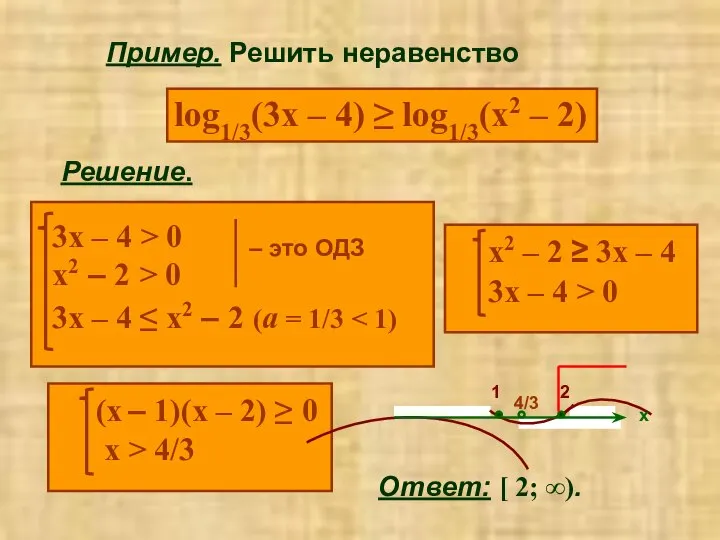
- 12. Пример. Решить неравенство log1/3(3x – 4) ≥ log1/3(x2 – 2) Решение. Ответ: [ 2; ∞).
- 13. Простейшие логарифмические неравенства.
- 14. І І І) Неравенства, требующие предварительных преобразований. 1) Находят ОДЗ неравенства. 2) Преобразуют неравенство к виду
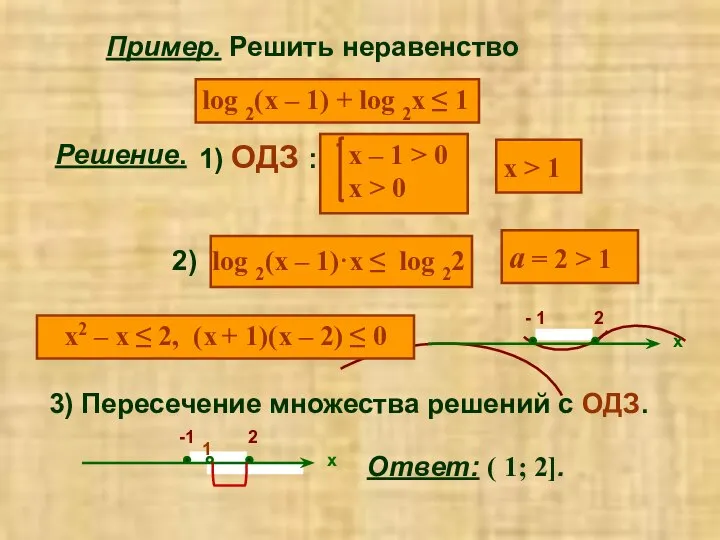
- 15. Пример. Решить неравенство log 2(x – 1) + log 2x ≤ 1 Решение. Ответ: ( 1;
- 16. Отсюда имеем lg x lg x т. к. a = 10 > 1, x >0, то
- 17. IV. Решение логарифмических неравенств, содержащих переменную в основании логарифма Теорема 1. Если а > 0, a
- 18. Решение логарифмических неравенств, содержащих переменную в основании логарифма Замечание- соглашение. Для упрощения записей целесообразно ввести символ
- 19. Пример 1. Решите неравенство logx+7(2x2-6x+8)≤logx+7(x2+x-2). Решение: logx+7(2x2-6x+8) ≤ logx+7(x2+x-2) Так как D -6 -7 -2 1
- 20. Следствие 2. При допустимых значениях a и b неравенство logab v 0 равносильно неравенству (a -1)(b
- 22. Теорема 2. При допустимых значениях a ,b , c, d неравенство logab logcd v 0 равносильно
- 23. При допустимых значениях a ,b , c неравенство logab - logcb v 0 равносильно неравенству (a
- 25. Скачать презентацию



















 Newton’s binomial formula
Newton’s binomial formula Критерии теории игр
Критерии теории игр Определители и их свойства
Определители и их свойства Тренажёр. Таблица умножения. «С Барби за покупками»
Тренажёр. Таблица умножения. «С Барби за покупками» Десятичные дроби. 5 класс
Десятичные дроби. 5 класс Математическая конференция 6а класса
Математическая конференция 6а класса Легенды о Пифагоре и его теореме
Легенды о Пифагоре и его теореме ЕГЭ-2018. Задания 1 - 12
ЕГЭ-2018. Задания 1 - 12 Корреляция. Причинность. Детерминизм
Корреляция. Причинность. Детерминизм В царстве «чисел-великанов». Илтакова Александра ученица 6 класса Зун-Муринской СОШ
В царстве «чисел-великанов». Илтакова Александра ученица 6 класса Зун-Муринской СОШ Элементы интегрального исчисления
Элементы интегрального исчисления Решение системы уравнений y0=2х2
Решение системы уравнений y0=2х2 Умножение и деление на 2, 3 и 4
Умножение и деление на 2, 3 и 4 Презентация на тему Размещения и сочетания
Презентация на тему Размещения и сочетания  Внеклассное мероприятие. Путешествие в мир многогранников
Внеклассное мероприятие. Путешествие в мир многогранников Решение задач на проценты. 6 класс. Урок 1
Решение задач на проценты. 6 класс. Урок 1 Биквадратные уравнения
Биквадратные уравнения Признаки параллельности прямых
Признаки параллельности прямых Зеркальная симметрия и параллельный перенос
Зеркальная симметрия и параллельный перенос Числовые промежутки
Числовые промежутки Графы и их применение к решению задач
Графы и их применение к решению задач Геометрическая прогрессия
Геометрическая прогрессия График функции у =f(x) и касательная. Задачи
График функции у =f(x) и касательная. Задачи Регулярные выражения
Регулярные выражения Дидактическая игра как средство повышения эффективности урока математики
Дидактическая игра как средство повышения эффективности урока математики Презентация по математике "Применение интеграла к решению физических задач" - скачать бесплатно
Презентация по математике "Применение интеграла к решению физических задач" - скачать бесплатно 25.02.2010г. Закрепление темы «Правила дифференцирования» Дернова А.М. Учитель математикиIкв.к. МБОУ «Новотроицкая СОШ»
25.02.2010г. Закрепление темы «Правила дифференцирования» Дернова А.М. Учитель математикиIкв.к. МБОУ «Новотроицкая СОШ» Упражнения по планиметрии на готовых чертежах. VII класс
Упражнения по планиметрии на готовых чертежах. VII класс