Содержание
- 2. Унарные отношения Отношения – один из способов задания взаимосвязей между элементами множества. Унарные (одноместные) отношения отражают
- 3. Бинарные (двухместные отношения) используются для определения каких-либо взаимосвязей, которыми характеризуются пары элементов во множестве М. Например,
- 4. n-местное отношение
- 5. Бинарные отношения Пример. Пусть . Рассмотрим отношение R⊆ A × A , R- множество всех пар
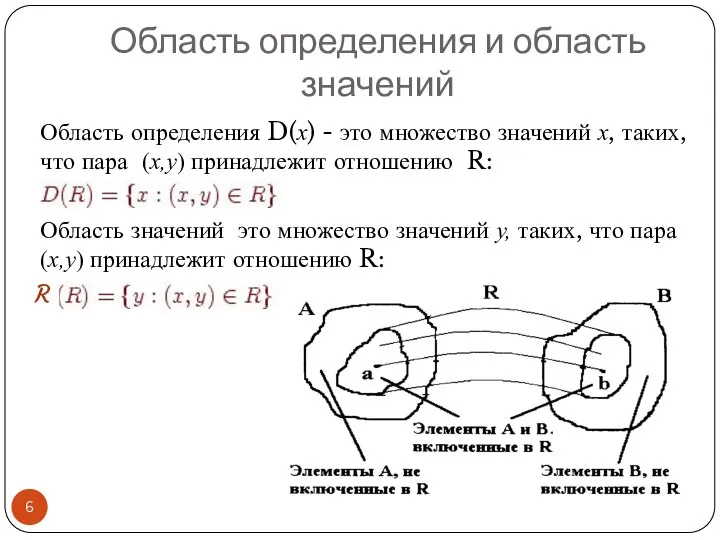
- 6. Область определения и область значений Область определения D(x) - это множество значений x, таких, что пара
- 7. Пример. Для отношения рассмотренного в предыдущем примере, область определения и область значений будут соответственно равны: и
- 8. Способы задания отношений 2. Характеристическим свойством. Например, 3. Графически. Например, R ={(1,5), (2,4), (3,6), (6,2)} на
- 9. Способы задания отношений
- 10. Пример. R ={(1,5), (2,4), (3,6), (6,2)} на R⊆ Х2, Х = {1,2,3,4,5,6} Способы задания отношений
- 11. Способы задания отношений
- 12. Матрица отношения будет иметь вид: Способы задания отношений
- 13. Способы задания отношений
- 14. Способы задания отношений
- 15. Способы задания отношений 4. на рис.
- 16. Рассмотрим подробнее графический способ задания отношений. Графические методы задания отношения: Координатный метод; Линейно-координатный метод; Линейный метод;
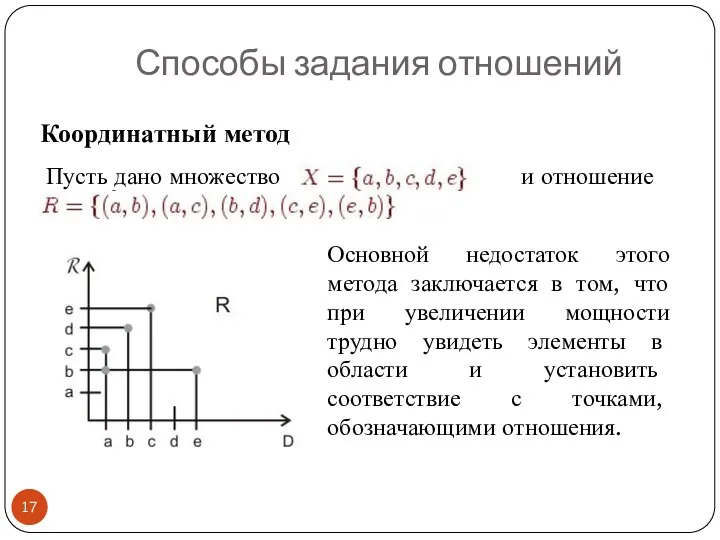
- 17. Координатный метод Способы задания отношений Пусть дано множество и отношение R⊆X2: Основной недостаток этого метода заключается
- 18. Линейно-координатный метод Способы задания отношений Представим то же отношение На множестве линейно-координатным методом. Недостаток этого метода
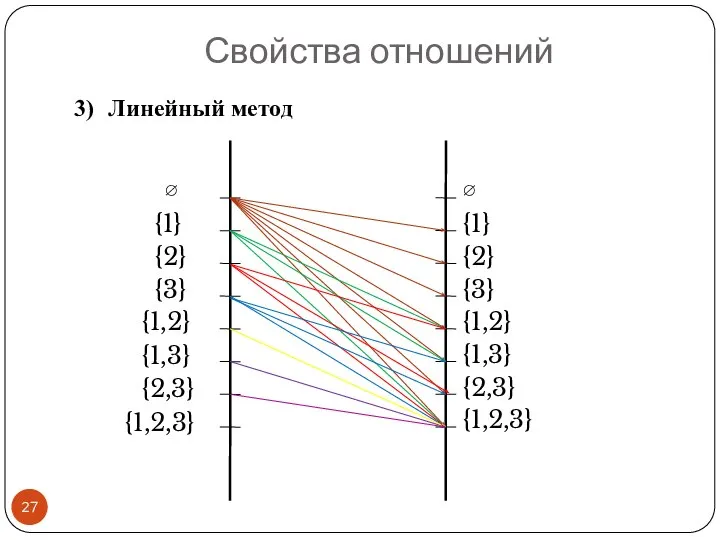
- 19. Линейный метод Используя параллельные вертикальные линии для D и R получаем диаграммы, в которых стрелки не
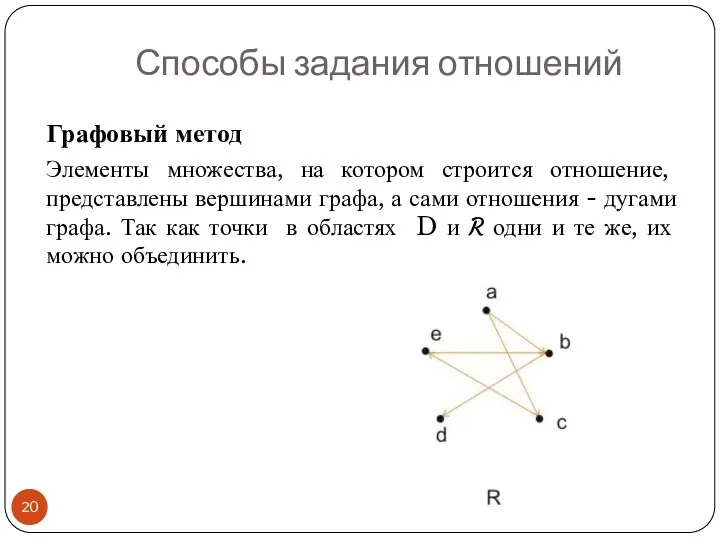
- 20. Графовый метод Элементы множества, на котором строится отношение, представлены вершинами графа, а сами отношения - дугами
- 21. Задача. По матрице представить отношение списком, графически Способы задания отношений
- 22. Свойства отношений
- 23. Свойства отношений
- 24. Пример. Пусть Определено на множестве Зададим списком: Свойства отношения R: рефлексивно, так как х/х=1 для ∀х∈N
- 25. Свойства отношений 1 2 3 4 7 6 5 8 9
- 26. Пример. На булеане множества М={1, 2, 3} задано отношение R – «являться собственным подмножеством». Задать списком,
- 27. Свойства отношений ∅ ∅ {1} {2} {3} {1,2} {1,3} {2,3} {1,2,3} {1} {3} {2} {1,2} {1,3}
- 28. Свойства отношений ∅ {1} {2} {3} {1,2} {1,3} {2,3} {1,2,3} Графовый метод
- 29. Свойства отношения R – «быть собственным подмножеством»: Не является рефлексивным Антирефлексивно, так как любое множество не
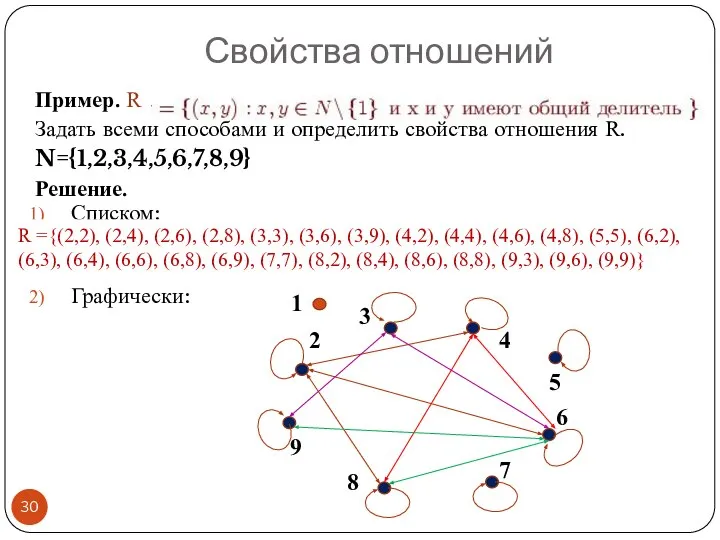
- 30. Пример. R Задать всеми способами и определить свойства отношения R. N={1,2,3,4,5,6,7,8,9} Решение. Списком: Графически: Свойства отношений
- 31. Матрица отношения «иметь общий делитель» Свойства отношений
- 32. Свойства отношения R- «иметь общий делитель»: нерефлексивно, так как выполняется аRа ∀а∈R, кроме а=1; Не антирефлексивно;
- 33. Свойства отношений
- 34. Свойства отношений Матрица рефлексивного отношения имеет на главной диагонали 1 А на диаграмме графового представления рефлексивного
- 35. Свойства отношений На диаграмме графового представления антирефлексивного отношения ни для какого узла не существует стрелка-петля. Матрица
- 36. Свойства отношений
- 37. Свойства отношений В матрице симметричного отношения единицы симметричны относительно главной диагонали На диаграмме графового представления симметричного
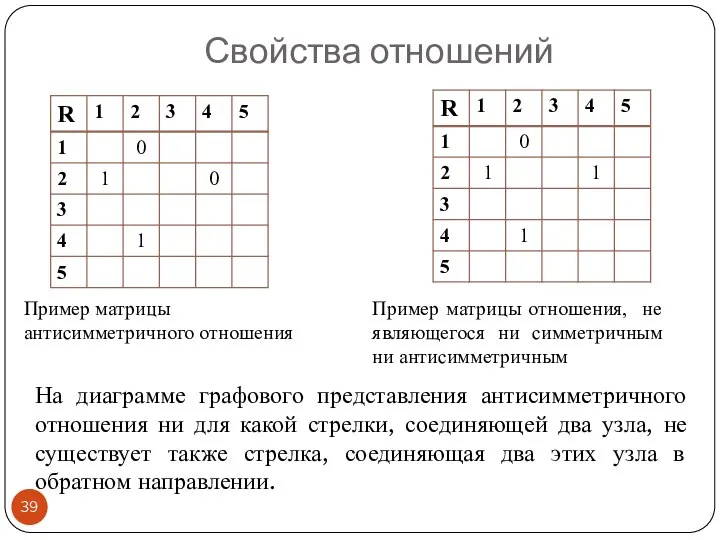
- 38. Свойства отношений Пример матрицы антисимметричного отношения
- 39. На диаграмме графового представления антисимметричного отношения ни для какой стрелки, соединяющей два узла, не существует также
- 40. 5) На диаграмме графового представления транзитивного отношения для каждой пары узлов a и c, связанных последовательностью
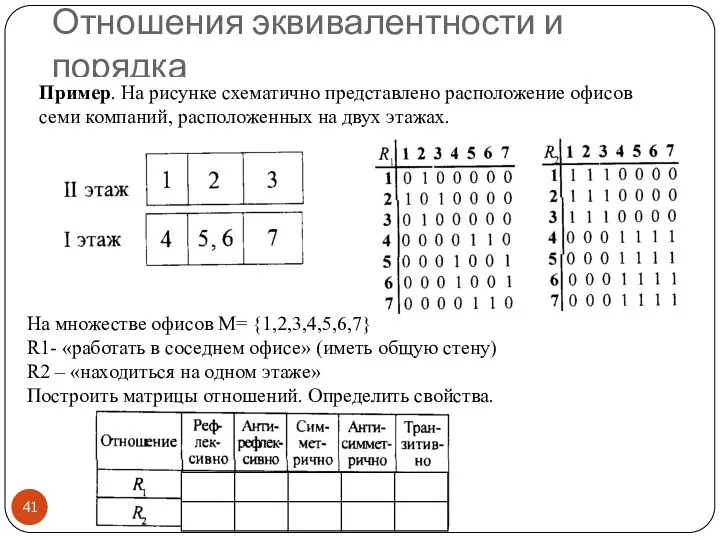
- 41. Отношения эквивалентности и порядка Пример. На рисунке схематично представлено расположение офисов семи компаний, расположенных на двух
- 42. Определение: Отношение эквивалентности– это бинарное отношение на множестве Х, удовлетворяющее следующим условиям: Рефлексивность (xRx) Симметричность (xRy
- 43. Отношение эквивалентности Пример. R- «быть равным» на множестве натуральных чисел. Свойства: Рефлексивно, т.к. а=а, ∀а∈N; Симметрично,
- 44. Примеры отношений эквивалентности: Отношение «быть равным», «иметь один и тот же остаток от деления на конкретное
- 45. Отношение толерантности Определение: Отношением толерантности (или просто толерантностью) на множестве X называется бинарное отношение, удовлетворяющее свойствам
- 46. Отношения «быть другом», «быть знакомым», - отношения толерантности, так как они рефлексивны, симметричны, но не транзитивны.
- 47. Отношения порядка Множество М, которое обладает отношением порядка, называется упорядоченным. Отношение порядка антисимметричность транзитивность + рефлексивность
- 48. Отношение строгого порядка Определение: Отношение строгого порядка– это бинарное отношение на множестве Х, удовлетворяющее следующим условиям:
- 49. Отношение нестрогого порядка Определение: Отношение нестрогого порядка– это бинарное отношение на множестве Х, удовлетворяющее следующим условиям:
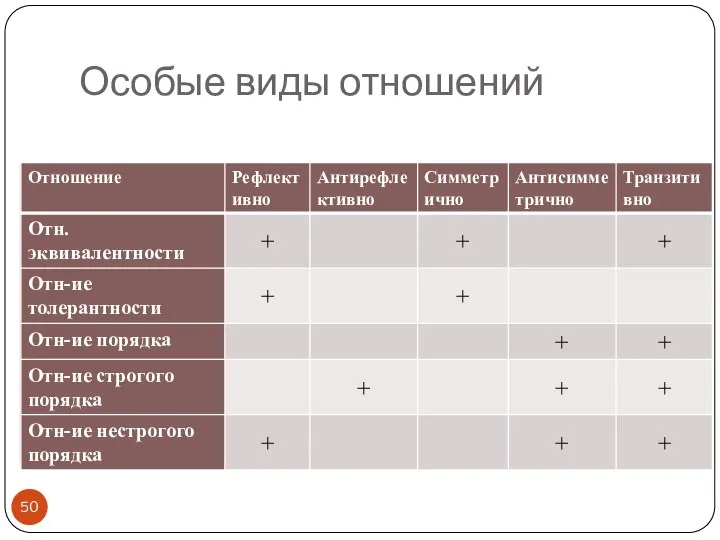
- 50. Особые виды отношений
- 51. Задача 2. Дан граф некоторого отношения. Дополните его минимальным числом стрелок так, чтобы оно превратилось в
- 52. Задача 3. Назовем два слова сходными, если они состоят из одинакового числа букв, причем либо совпадают,
- 54. Скачать презентацию











































 Непрерывные функции
Непрерывные функции Аттестационная работа. Программа курса внеурочной деятельности Живая математика
Аттестационная работа. Программа курса внеурочной деятельности Живая математика Старинный способ решения задач на смеси и сплавы
Старинный способ решения задач на смеси и сплавы Координатная плоскость
Координатная плоскость Линейные неравенства
Линейные неравенства Задачи на построение сечений в тетраэдре и параллелограмме
Задачи на построение сечений в тетраэдре и параллелограмме Математическая жизнь класса в графиках и диаграммах
Математическая жизнь класса в графиках и диаграммах Пособие для самостоятельного обучения учащихся 5-6 классов Проценты. Основные задачи на проценты.
Пособие для самостоятельного обучения учащихся 5-6 классов Проценты. Основные задачи на проценты. Площадь правильного треугольника
Площадь правильного треугольника Числовые последовательности
Числовые последовательности Открытый урок в 1 классе по математике. Тема: Дециметр
Открытый урок в 1 классе по математике. Тема: Дециметр K-подмножества
K-подмножества Прямоугольник. Квадрат
Прямоугольник. Квадрат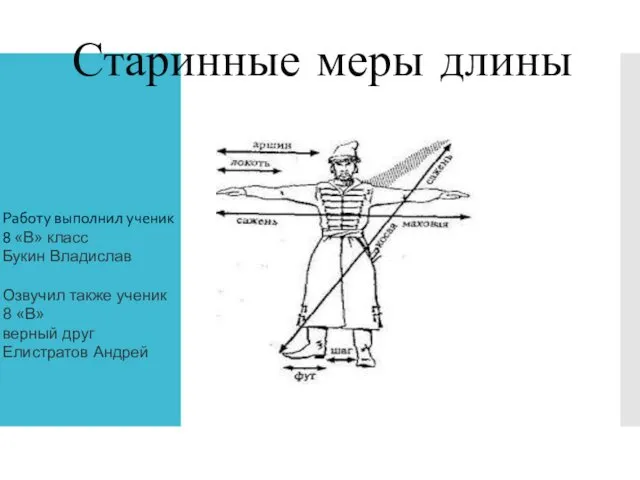 Старинные меры длины на Руси
Старинные меры длины на Руси Марковские цепи
Марковские цепи Презентация на тему Кто хочет стать отличником Математическая игра
Презентация на тему Кто хочет стать отличником Математическая игра  Решение уравнений (5 класс)
Решение уравнений (5 класс) Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Исследовательская работа на уроках математики Учитель математики Ледовская Евгения Николаевна
Исследовательская работа на уроках математики Учитель математики Ледовская Евгения Николаевна  Сумма углов треугольника
Сумма углов треугольника Моделирование систем и процессов. Марковские процессы. (Лекция 3)
Моделирование систем и процессов. Марковские процессы. (Лекция 3) Подготовка к контрольной работе по алгебре. (9 класс)
Подготовка к контрольной работе по алгебре. (9 класс) Алгоритмы линейного поиска. Тема 1
Алгоритмы линейного поиска. Тема 1 Свойства параллельных прямых
Свойства параллельных прямых Құрама есептер
Құрама есептер Урок математики
Урок математики Презентация по математике "Уравнения 1 класс" - скачать бесплатно
Презентация по математике "Уравнения 1 класс" - скачать бесплатно Справедливые и несправедливые игры с точки зрения теории вероятностей
Справедливые и несправедливые игры с точки зрения теории вероятностей