Содержание
- 2. Символическая логика она же символическая формируется в XIX веке, благодаря Готлобу Фреге и Бертрану Расселу состоит
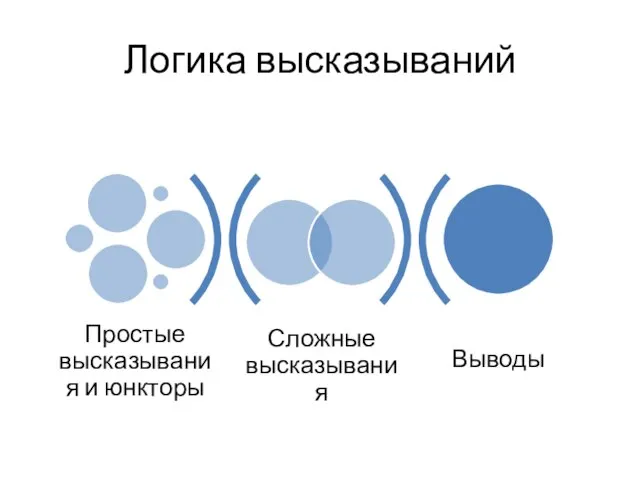
- 4. Логика высказываний
- 5. Высказывание мысль, выраженная повествовательным предложением, которая может быть истинной или ложной
- 6. Формальный аппарат А, В, С…. – пропозициональные переменные (формулы), отражающие независимый факт; ¬ – униарная связка-юнктор;
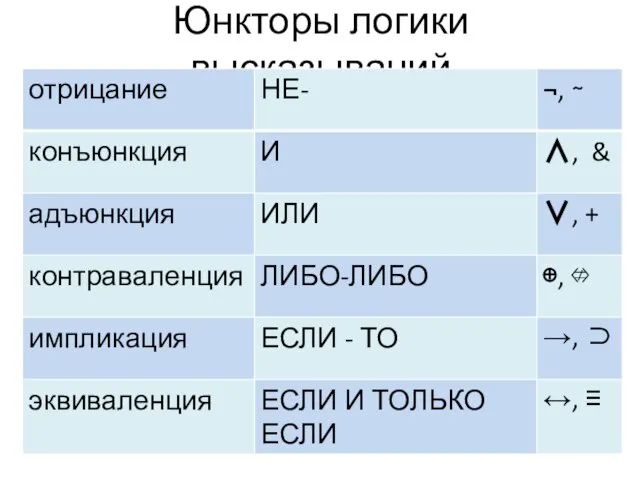
- 7. Юнкторы логики высказываний
- 8. Преобразование конъюнкции в дизъюнкцию (А ∧ В) = ¬(¬А ∨ ¬В) в импликацию (А ∧ В)
- 9. Преобразование дизъюнкции в конъюнкцию (А ∨ В) = ¬(¬А ∧ ¬В) в импликацию (А ∨ В)
- 10. Преобразование импликации в конъюнкцию (А → В) = ¬(А ∧ ¬В) в дизъюнкцию (А → В)
- 11. Преобразование строгой дизъюнкции в конъюнкцию (А ⊕ В) = (А ∨ В) ∧ (¬А ∨ ¬В)
- 12. Формулы тождественно-истинные (законы) истинные при всех наборах истинностных значений переменных тождественно-ложные (противоречия) ложные при всех наборах
- 13. Правило подстановки любую буквенную переменную в символическом выражении можно заменять на произвольную формулу Например, (p ∨
- 14. Законы символической логики дистрибутивности ассоциативности коммутативности двойственности контрапозиции импортации экспортации транспозиции исключения поглощения выявления
- 15. Закон ассоциативности (А ∧ (В ∧ С)) = ((А ∧ В) ∧ С) (А ∨ (В
- 16. Закон дистрибутивности для двух переменных (А ∧ (В ∨ С)) = (А ∧ В) ∨ (А
- 17. Закон двойственности для конъюнкции и дизъюнкции (А ∧ В) = ¬(¬А ∨ ¬В) (А ∨ В)
- 18. Закон контрапозиции (А → В) = (¬А → ¬В) ((А ∧ В) → С) = (¬С
- 19. Закон транспозиции ((А ∧ В) → С) = ((А ∧ ¬С) → ¬В) Закон исключения (А
- 20. Закон поглощения (А ∧ (А ∨ В)) = А (А ∨ (А ∧ В)) = А
- 21. результат реконструкции естественного языка Здесь есть точные правила построения высказываний (формул) и сложных имен (термов) Этот
- 22. Нелогические символы естественного языка Предикатор Предметные функторы Имя
- 23. Имена обозначают отдельный объект, бывают простые и сложные. Простые не содержат никакой информации об обозначаемых индивидах
- 24. Предметные функторы знаки так называемых предметных функций (функциональная константа) Наряду с математическими функциями «синус», «логарифм», «умножение»
- 25. Предикатор (предикатная константа) - выражение языка (слова и словосочетания), предметными значениями которого являются свойства (одноместные предикаторы)
- 26. Язык логики предикатов
- 27. Определение терма 1 любая предметная переменная и предметная константа – термы 2 если F – предметный
- 28. Пример а – «Аполлон» в – «Венера» f1 – «красавец» g2 – «молодой» f1(a) – Аполлон
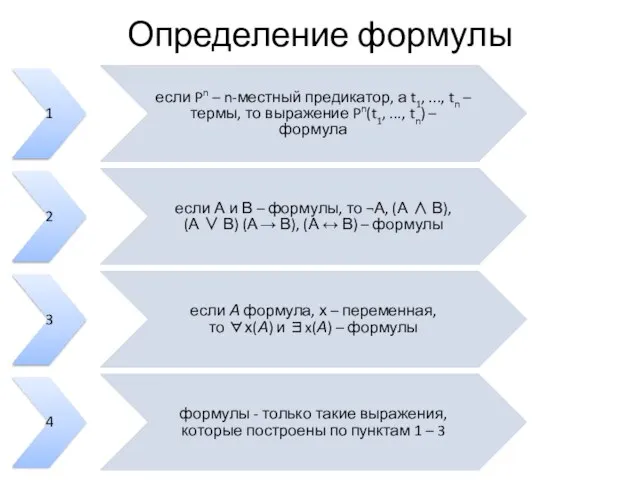
- 29. Определение формулы 1 если Pn – n-местный предикатор, а t1, ..., tn – термы, то выражение
- 30. Область действия квантора Если формула А имеет вид ∀хВ или ∃хВ, то областью действия квантора ∀
- 31. Пример «Если целое число больше 13, то его квадрат делится без остатка на 4 или на
- 32. Некоторые законы логики предикатов 1. Взаимовыразимость кванторов ∀хА ↔ ¬∃х¬А, ∃хА ↔ ¬∀х¬А. 2. Отрицание кванторов
- 33. Некоторые законы логики предикатов 4. Законы пронесения и вынесения кванторов а) конъюнкция ∀a(А ∧ В) ↔
- 34. Примеры «Все люди интересуются строением космоса», ∀х(Р1(х) → Q1(х, f(a)) где Р1 – «быть человеком», Q1
- 35. Исчисление естественного вывода порождение одних формул из других Здесь нет аксиом. Знание не истинное, а доказуемое.
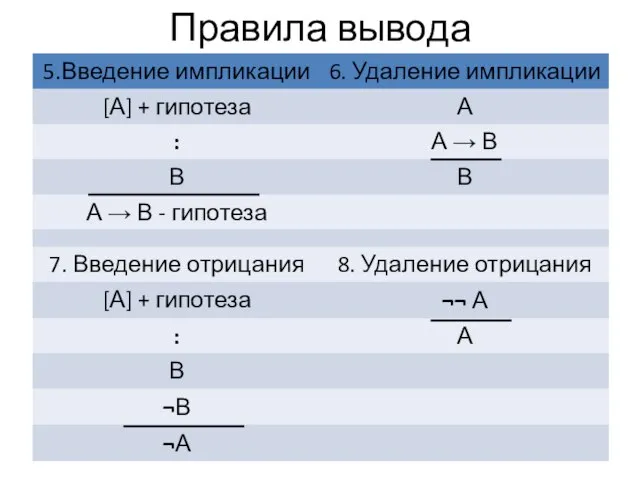
- 36. Правила вывода
- 37. Правила вывода
- 38. Пример «Семён сидит дома или разговаривает по телефону. Если он сидит дома, то он скучает. Он
- 40. Скачать презентацию

































 Диаграммы Чтение диаграмм. (6 класс)
Диаграммы Чтение диаграмм. (6 класс) Презентация по математике "Применение квадратичной функции в баллистике" - скачать
Презентация по математике "Применение квадратичной функции в баллистике" - скачать  Приращение функции
Приращение функции Перестановка слагаемых. Применение переместительного свойства
Перестановка слагаемых. Применение переместительного свойства Презентация по математике "Математика в повседневной жизни" - скачать
Презентация по математике "Математика в повседневной жизни" - скачать  Показательная функция, её свойства и график
Показательная функция, её свойства и график Основы теории случайных процессов
Основы теории случайных процессов Задачи на проценты
Задачи на проценты Геометрическая интерпретация комплексных чисел
Геометрическая интерпретация комплексных чисел Своя игра. 6 класс
Своя игра. 6 класс Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Задачи по теме «Призма и пирамида»
Задачи по теме «Призма и пирамида» Практическое применение интегралов в различных областях
Практическое применение интегралов в различных областях Моделирование, основные понятия и определения, виды и методы идентификации статических моделей
Моделирование, основные понятия и определения, виды и методы идентификации статических моделей Решение уравнений третьей степени различными способами
Решение уравнений третьей степени различными способами Наименьшее общее кратное
Наименьшее общее кратное Методы параметрического спектрального анализа. Оценка порядка АР-модели и сравнение оценок СПМ
Методы параметрического спектрального анализа. Оценка порядка АР-модели и сравнение оценок СПМ Тренажер «Домики». Состав числа в пределах 10
Тренажер «Домики». Состав числа в пределах 10 20171220_prezentatsiya_matematicheskiy_poezd
20171220_prezentatsiya_matematicheskiy_poezd Проецирование. Общие сведения о проецировании. Способы проецирования. Прямоугольное проецирование
Проецирование. Общие сведения о проецировании. Способы проецирования. Прямоугольное проецирование Деление дробей. Французский математик и физик Паскаль
Деление дробей. Французский математик и физик Паскаль Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами Увеличение (уменьшение) числа в 10, 100, 1000 раз (4 класс)
Увеличение (уменьшение) числа в 10, 100, 1000 раз (4 класс) Числовые характеристики случайной величины. Лекция 2
Числовые характеристики случайной величины. Лекция 2 Признаки подобия треугольников. Решение задач
Признаки подобия треугольников. Решение задач Сума кутів трикутника. Урок розв'язування задач. 7 клас
Сума кутів трикутника. Урок розв'язування задач. 7 клас Реляционная алгебра
Реляционная алгебра Несложное показательное, логарифмическое или иррациональное уравнение
Несложное показательное, логарифмическое или иррациональное уравнение