Содержание
- 2. Цель проекта: Совершенствовать свои умения и навыки при решении уравнений; Познакомиться с историческими сведениями о решении
- 3. Омар Хайям (ок. 1048- ок. 1123) Описал всевозможные виды уравнений третьей степени и рассмотрел сложные и
- 4. В начале XVI века в крупных торговых городах Северной Италии были популярны математические состязания. Математики публично
- 5. Николо Тарталья (ребёнок из очень бедной семьи, мать не могла платить за образование, поэтому мальчик в
- 6. Джероламо Кардано (медик) занимался астрологией, составлял гороскопы. Кардано неоднократно обращался к Тарталье с просьбой сообщить ему
- 7. x³-3x-2=0 1) Разложение на множители: x³-3x-2=x³+x²-x²-x-2x-2=0 x²(x+1)-x(x+1)-2(x+1)=0 (x+1)(x²-x-2)=0 x=-1 D=1+8=9 x₁=2 x₂=-1 Ответ: -1; 2.
- 8. 2) Решение с помощью теоремы Безу: x³-3x-2=0 x³-3x-2=0 (-1)³ -3(-1)-2=0 x=-1 x³-3x-2 x+1 x³+x² x²-x-2 -x²-3x
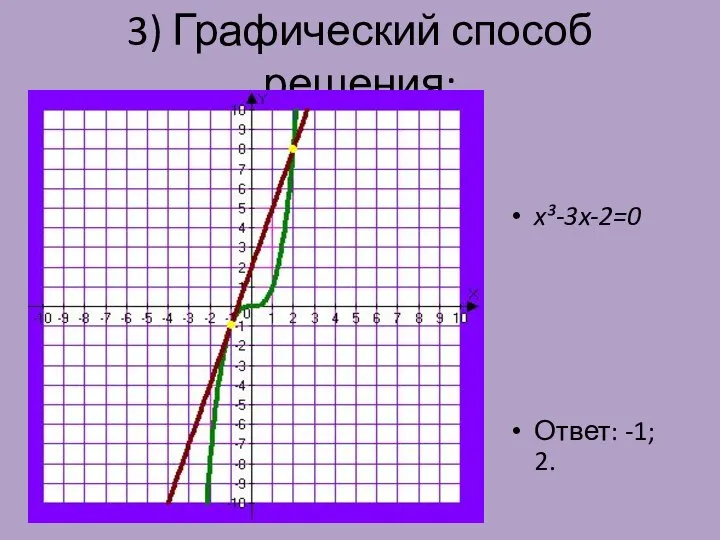
- 9. 3) Графический способ решения: x³-3x-2=0 Ответ: -1; 2.
- 10. x³-7x+6=0 1) Разложение на множители: x³-7x+6=0 x(x²-1)-6(x-1)=0 x(x-1)(x+1)-6(x-1)=0 (x²+x-6)(x-1)=0 D=1+24=25 x-1=0 x₁=2 x=1 x₂=3 Ответ: -3;
- 11. 2) Решение с помощью теоремы Безу: 1³-7+6=0 1³-7+6=0 x³-7x+6 x-1 x³-x² x²+x-6 x²-7x -x²+x -6x+6 -6x+6
- 12. 3) Графический способ решения: Ответ: -3; 1; 2.
- 13. x³-13x+12=0 1) Разложение на множители: x³-13x+12=0 x³-x-12x+12=0 x(x²-1)-12(x-1)=0 x(x-1)(x+1)-12(x-1)=0 (x²+x-12)(x-1)=0 D=1+48=49 x=1 x₁=3 x₂=-4 Ответ: -4;
- 14. 2) Решение с помощью теоремы Безу: x³-13x+12=0 x³-13x+12=0 1-13+12=0 x=1 x³-13x+12 x-1 x³-x² x²+x-12 x²-13x x²-x
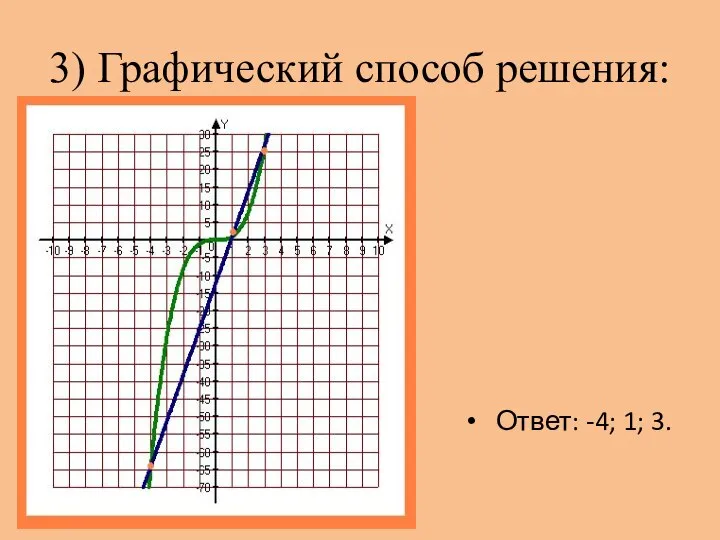
- 15. 3) Графический способ решения: Ответ: -4; 1; 3.
- 16. 2x³+x²-3=0 1) Разложение на множители: 2x³+x²-3=0 3x³-x³+x²-3=0 3(x³-1)-x²(x-1)=0 3(x-1)(x²+x+1)-x²(x-1)=0 (x-1)(3x²+3x+3-x²)=0 (x-1)(2x²+3x+3)=0 x=1 2x²+3x+3=0 D=9-24=-15 Ответ: 1.
- 17. 2) Решение с помощью теоремы Безу: 2x³+x²-3=0 2x³+x²-3 x-1 2x³-2x² 2x²+3x+3 3x²-3 3x²-3x 3x-3 3x-3 0
- 19. Скачать презентацию














 Весь курс геометрии. (7 класс)
Весь курс геометрии. (7 класс) Матрицы, операции над матрицами
Матрицы, операции над матрицами Компьютерные технологии принятия решений в формализованных и неформализованных задачах
Компьютерные технологии принятия решений в формализованных и неформализованных задачах Своя игра по математике
Своя игра по математике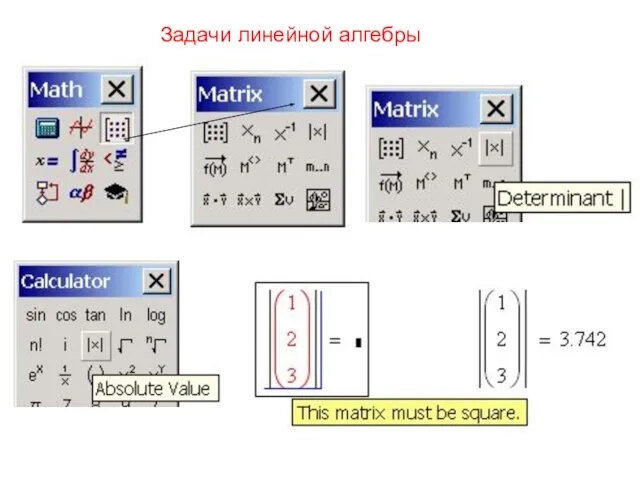 Задачи линейной алгебры. Решение дифференциальных уравнений в MathCAD
Задачи линейной алгебры. Решение дифференциальных уравнений в MathCAD Квадратичная функция ее график и свойства
Квадратичная функция ее график и свойства Определение подобных треугольников
Определение подобных треугольников Теорема Пифагора. Теорема, обратная к теореме Пифагора
Теорема Пифагора. Теорема, обратная к теореме Пифагора Теорема Пифагора
Теорема Пифагора Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Сечения тетраэдра
Сечения тетраэдра Факультативное занятие. Лабиринт. 6 класс
Факультативное занятие. Лабиринт. 6 класс Структурные средние
Структурные средние Дұрыс және бүрыс бөлшектер
Дұрыс және бүрыс бөлшектер Тест по математике! Начнём. Сокращать дроби!
Тест по математике! Начнём. Сокращать дроби! Построение сечений многогранников
Построение сечений многогранников Разложение квадратного трехчлена на множители. Теорема Виета
Разложение квадратного трехчлена на множители. Теорема Виета Значение переменной после выполнения алгоритма
Значение переменной после выполнения алгоритма Взвешенный и обобщенный МНК. Неоднородность. Дамми-переменные
Взвешенный и обобщенный МНК. Неоднородность. Дамми-переменные Основные законы теории вероятности
Основные законы теории вероятности Математический тренажёр «Наряжаем ёлочку». Случаи сложения и вычитания вида 26+4, 30-7
Математический тренажёр «Наряжаем ёлочку». Случаи сложения и вычитания вида 26+4, 30-7 Математический марафон
Математический марафон Descriptive statistics. Frequency distributions and their graphs. (Section 2.1)
Descriptive statistics. Frequency distributions and their graphs. (Section 2.1) Математический анализ Составитель: Никулина Л.С., старший преподаватель кафедры Математики и Моделирования
Математический анализ Составитель: Никулина Л.С., старший преподаватель кафедры Математики и Моделирования  Периметр треугольника
Периметр треугольника В заповедном лесу. Состав чисел первого десятка
В заповедном лесу. Состав чисел первого десятка Симметрия вокруг нас
Симметрия вокруг нас Прикидка результата действий. Цифры разряда, до которого выполняется округление. (5 класс)
Прикидка результата действий. Цифры разряда, до которого выполняется округление. (5 класс)