Содержание
- 2. Определение множества Величиной называется все что может быть измерено и выражено числом. Множеством называется совокупность некоторых
- 3. «Множество есть многое, мыслимое нами как единое». Основоположник теории множеств немецкий математик Георг Кантор (1845-1918)
- 4. С понятием множества мы соприкасаемся прежде всего тогда, когда по какой-либо причине объединяем по некоторому признаку
- 5. Примеры множеств: множество учащихся в данной аудитории; множество людей, живущих на нашей планете в данный момент
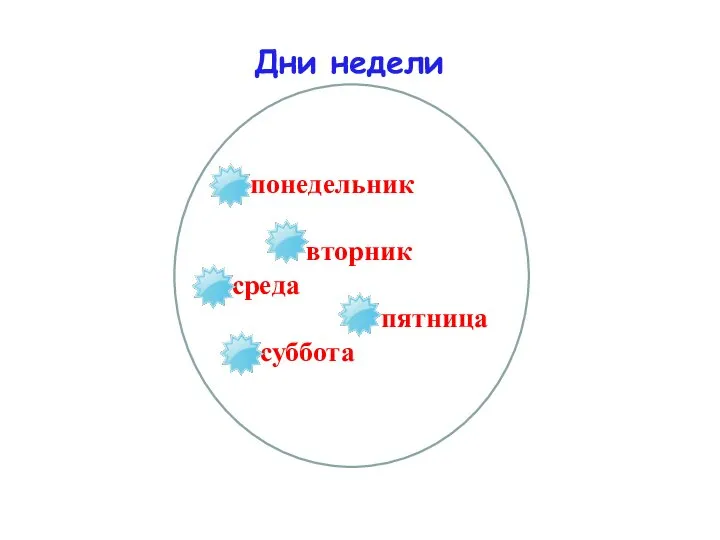
- 6. понедельник вторник среда пятница суббота Дни недели
- 7. Музыкальные инструменты
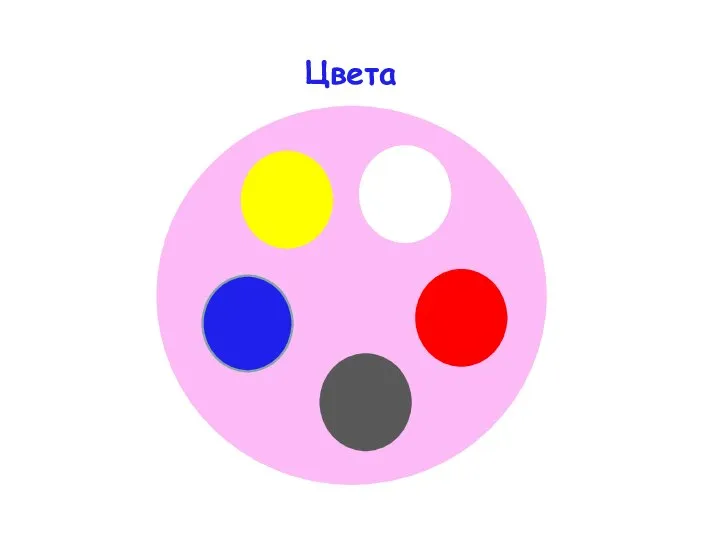
- 8. Цвета
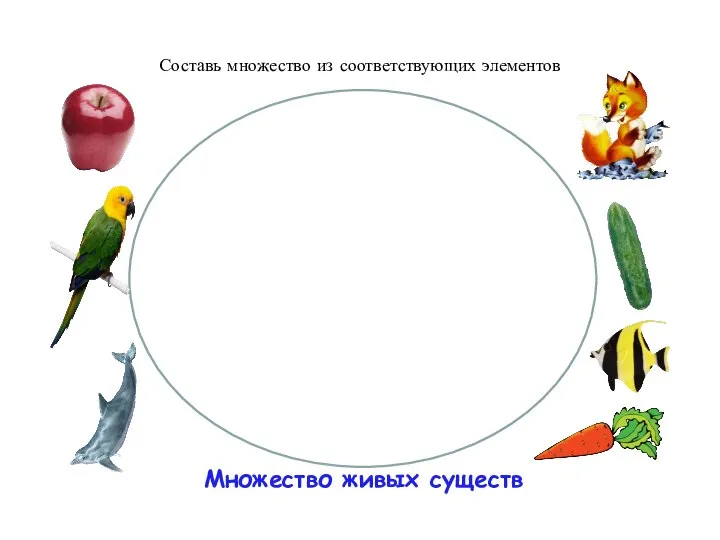
- 10. Множество живых существ Составь множество из соответствующих элементов
- 11. Объекты, из которых состоит множество, называются его ЭЛЕМЕНТАМИ. Если элемент x принадлежит множеству X, то записывают
- 12. Способы задания множеств Множество может быть задано перечислением всех его элементов или списком. В этом случае
- 13. Например, перечислением заданы следующие множества: А={1,2,3,5,7} — множество чисел Х={x1,x2,...,xn} — множество некоторых элементов x1,x2,...,xn N={1,2,...,n}
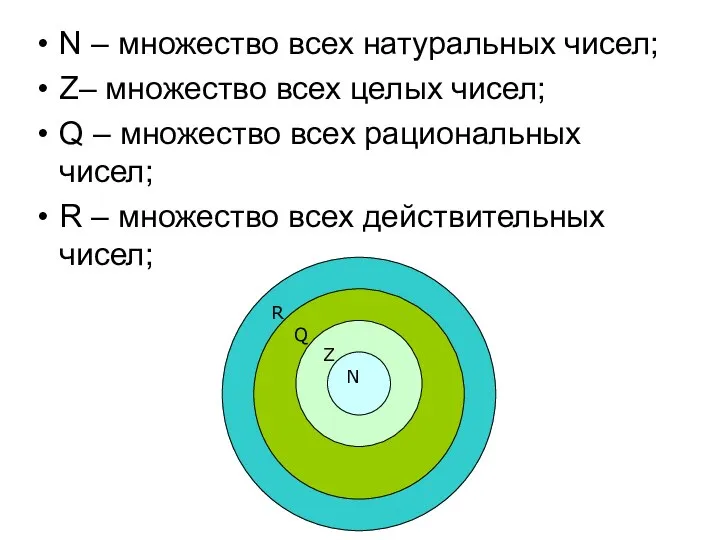
- 14. N – множество всех натуральных чисел; Z– множество всех целых чисел; Q – множество всех рациональных
- 15. Пример Мы говорим, что число 5 натуральное, т.е. утверждаем, что число 5 принадлежит множеству натуральных чисел.
- 16. Поставьте вместо звездочки знак так, чтобы получить правильное утверждение: 5 * N; –5 * Q; 3,14
- 17. Задайте перечислением элементов множество: 1) A = {x | x ∈ N, x2 – 4 =
- 18. По числу элементов, входящих в множество, множества делятся на три класса: 1 – конечные, 2 –
- 19. Если элементы множества можно сосчитать, то множество является КОНЕЧНЫМ Пример Множество гласных букв в слове “математика”
- 20. Если элементы множества сосчитать невозможно, то множество БЕСКОНЕЧНОЕ Пример Множество натуральных чисел бесконечно. Пример Множество точек
- 21. Примеры 1). множество, содержащее 6 элементов (конечное множество). 2). бесконечное счетное множество. 3). множество, содержащее 5
- 22. В теории множеств отдельно вводится множество, которое не содержит ни одного элемента. Такое множество называется пустым
- 23. Множество, не содержащее ни одного элемента, называется ПУСТЫМ. Символически оно обозначается знаком ∅ Пример Множество действительных
- 24. Мощность множества Число элементов конечного множества называют мощностью этого множества и обозначают символом Card A или
- 25. В любой конкретной задаче приходится иметь дело только с подмножествами некоторого, фиксированного для данной задачи, множества.
- 26. Отношения между множествами Наглядно отношения между множествами изображают при помощи особых чертежей, называемых КРУГАМИ ЭЙЛЕРА (или
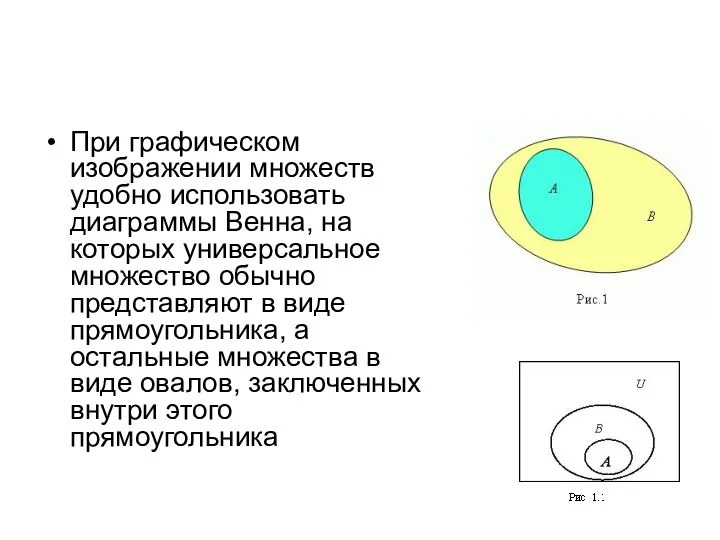
- 27. При графическом изображении множеств удобно использовать диаграммы Венна, на которых универсальное множество обычно представляют в виде
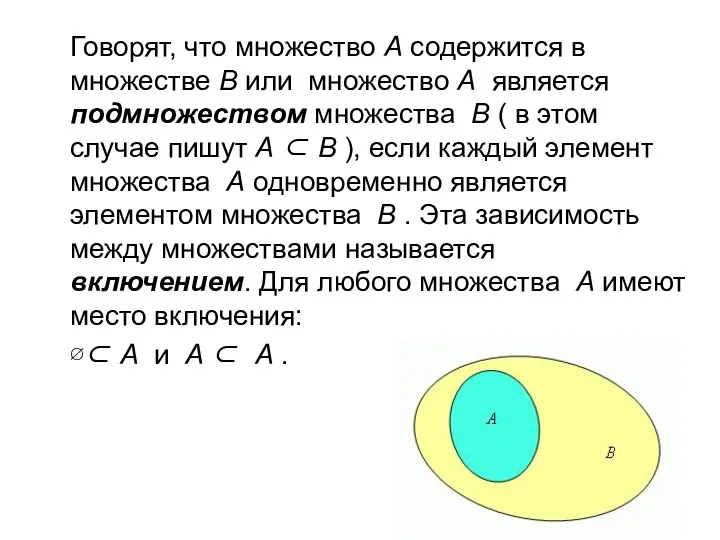
- 28. Множество A называется подмножеством множества B, если любой элемент множества A принадлежит множеству B. При этом
- 29. Говорят, что множество А содержится в множестве В или множество А является подмножеством множества В (
- 30. Определить как между собой соотносятся множества A = {1, 2, 3, 5, 7}, B ={1, 3,
- 31. Количество подмножеств Если мощность множества n, то у этого множества 2n подмножеств. А={1,2} Подмножества А: {∅},
- 32. Количество подмножеств В={1,3,5} Подмножества В: {∅}, {1}, {3}, {5}, {1,3}, {1,5}, {5,3}, {1,3,5} С={а,и,е,о} Подмножества С:
- 33. Два множества А и В называются равными ( А = В ), если они состоят из
- 34. Операции над множествами Два множества А и В равны (А=В), если они состоят из одних и
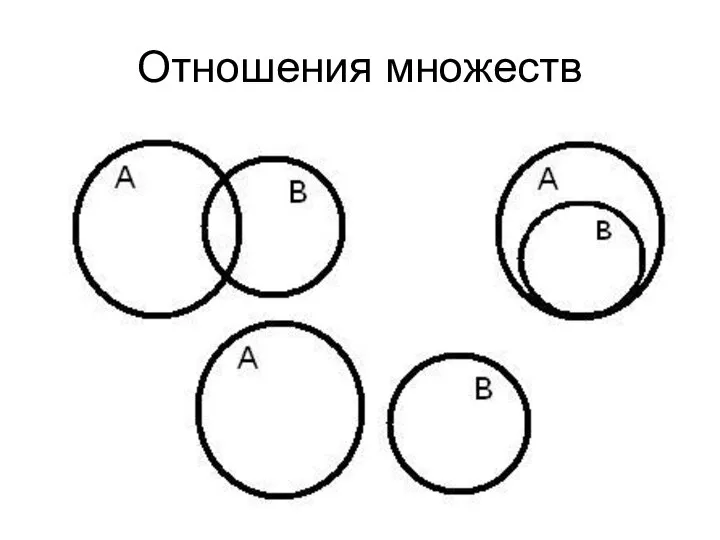
- 35. Отношения множеств
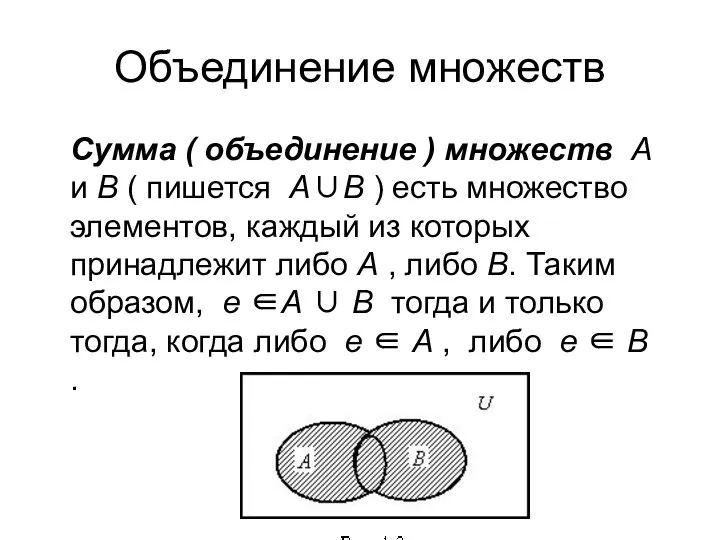
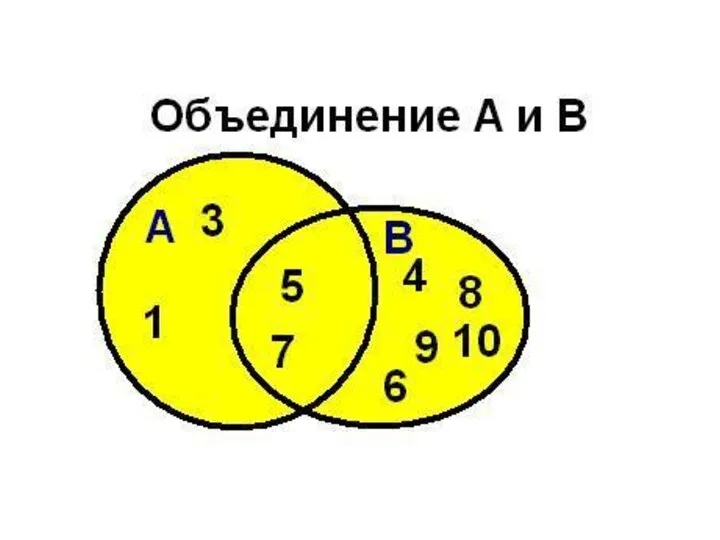
- 36. Объединение множеств Сумма ( объединение ) множеств А и В ( пишется А∪В ) есть множество
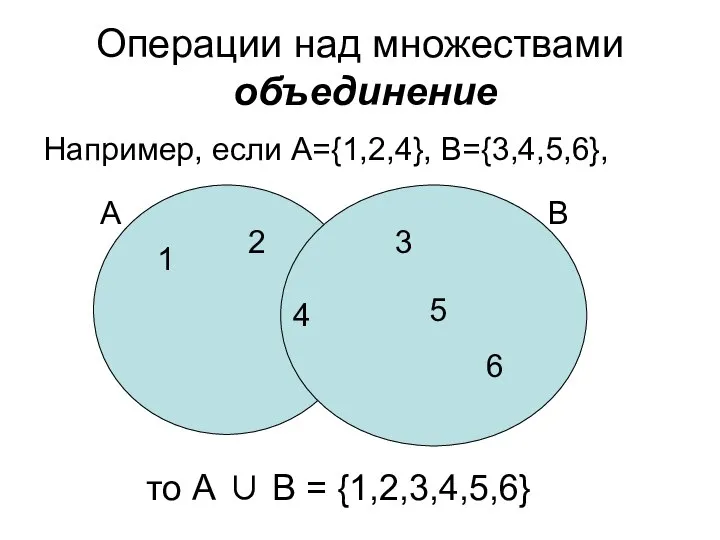
- 37. Операции над множествами объединение Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6} 1 2
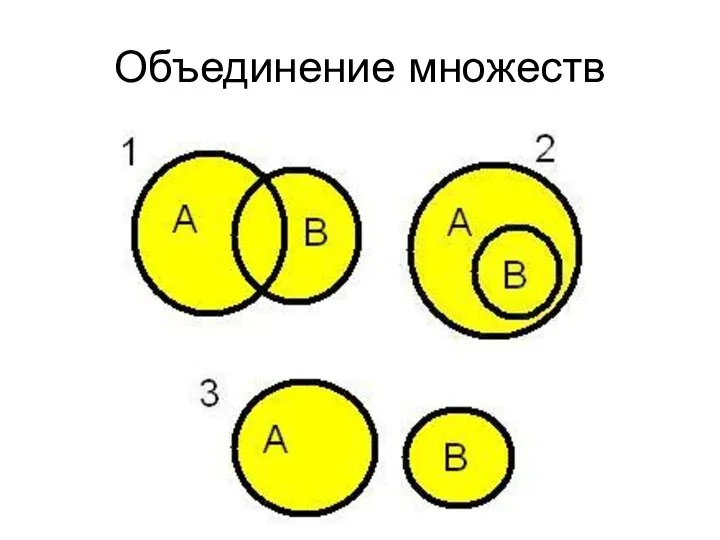
- 38. Объединение множеств
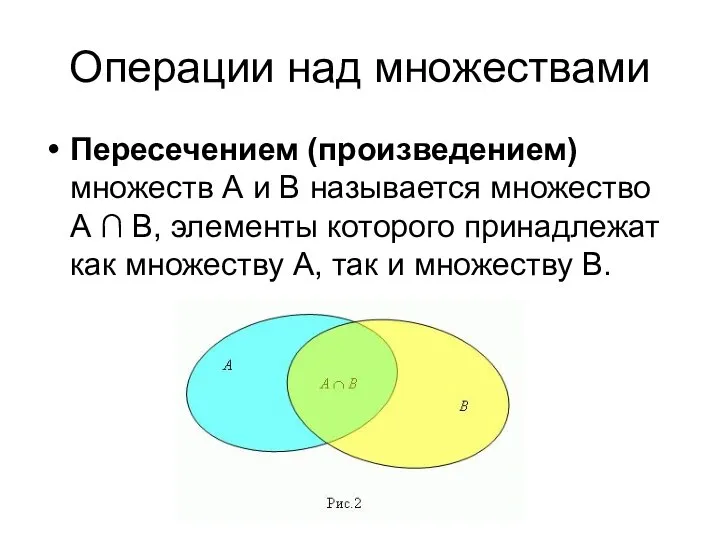
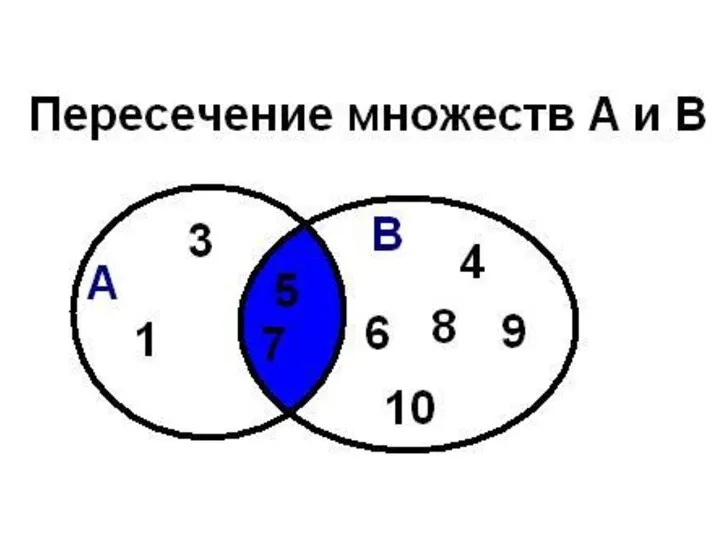
- 39. Операции над множествами Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого
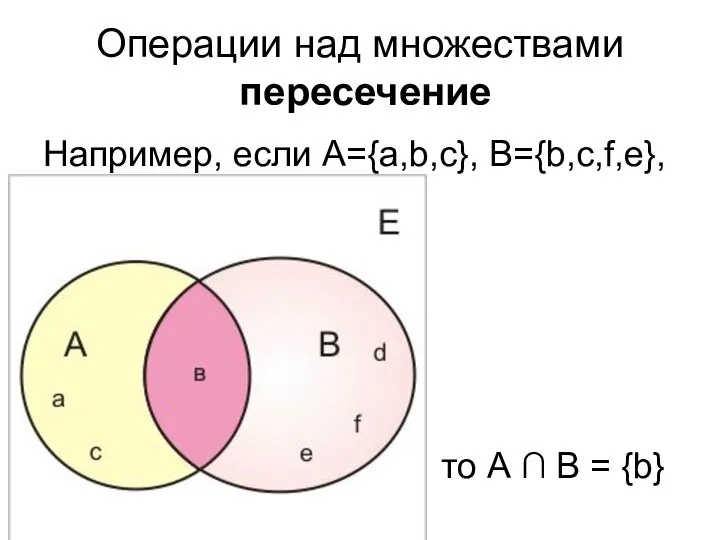
- 40. Операции над множествами пересечение Например, если А={a,b,c}, B={b,c,f,e}, то А ∩ В = {b}
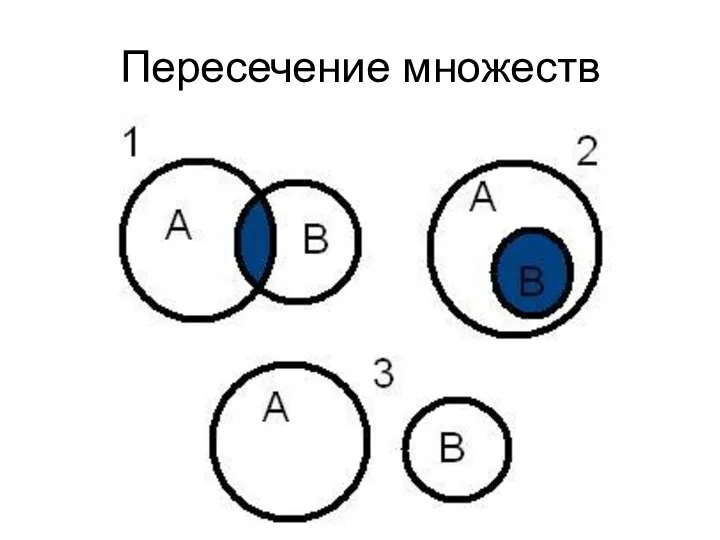
- 41. Пересечение множеств
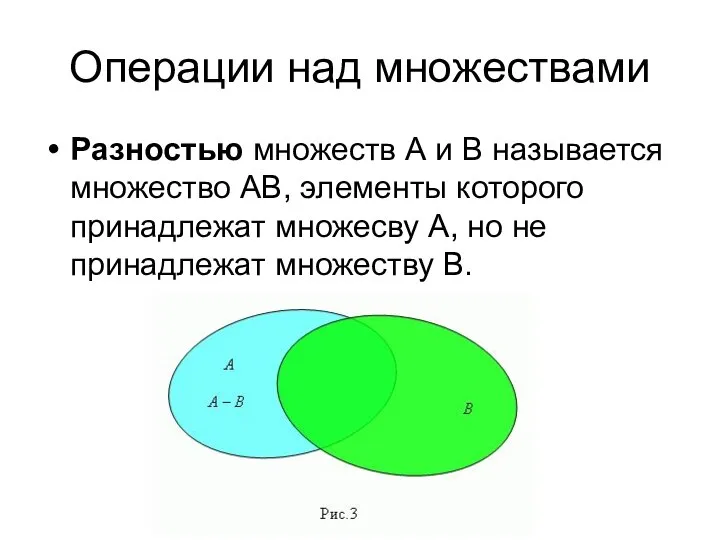
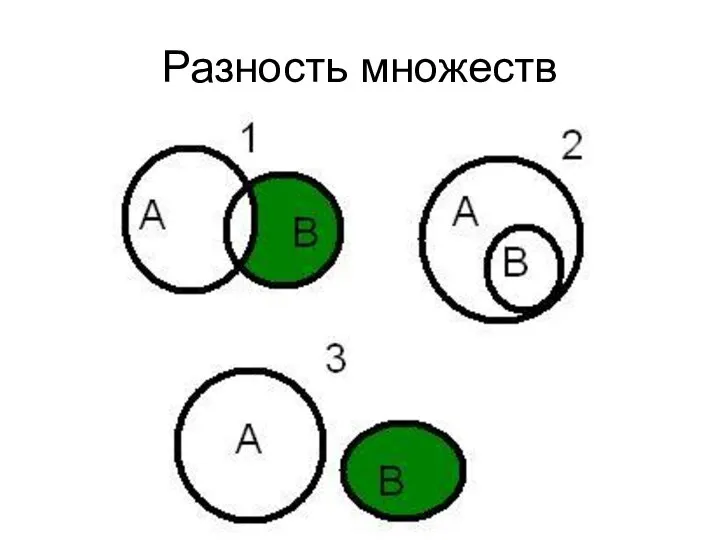
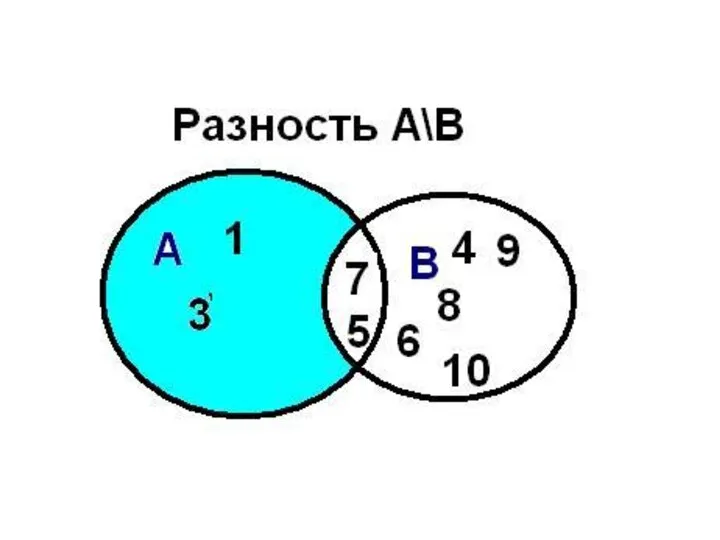
- 42. Операции над множествами Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А,
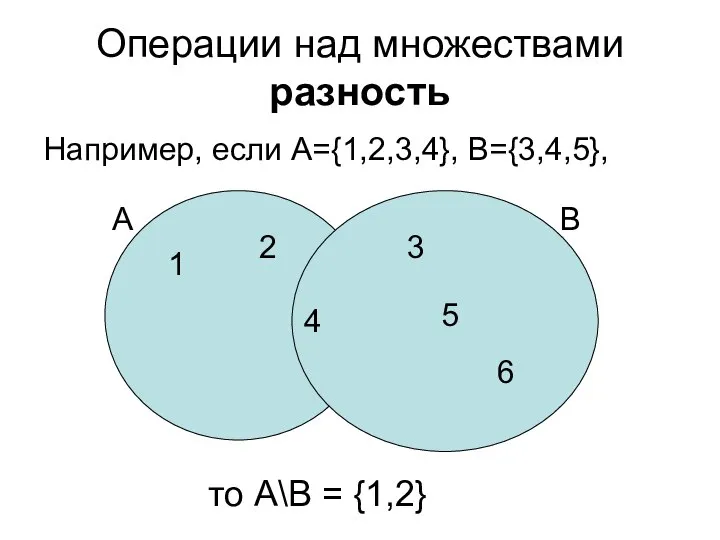
- 43. Операции над множествами разность Например, если А={1,2,3,4}, B={3,4,5}, то А\В = {1,2} 1 2 4 А
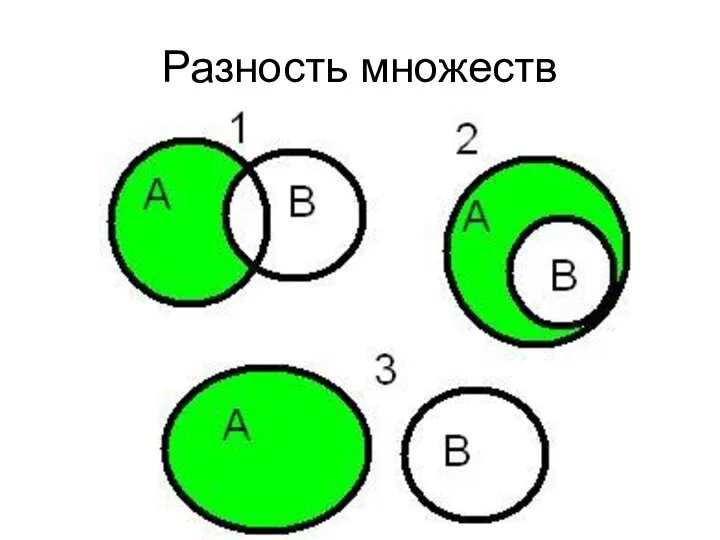
- 44. Разность множеств
- 45. Разность множеств
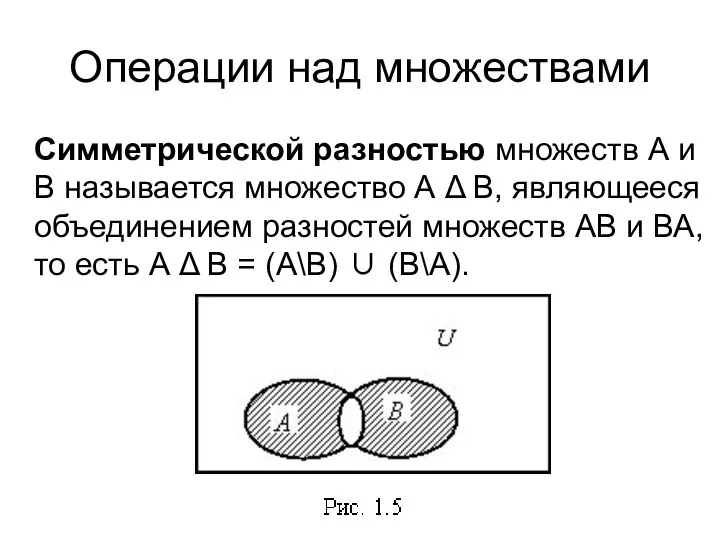
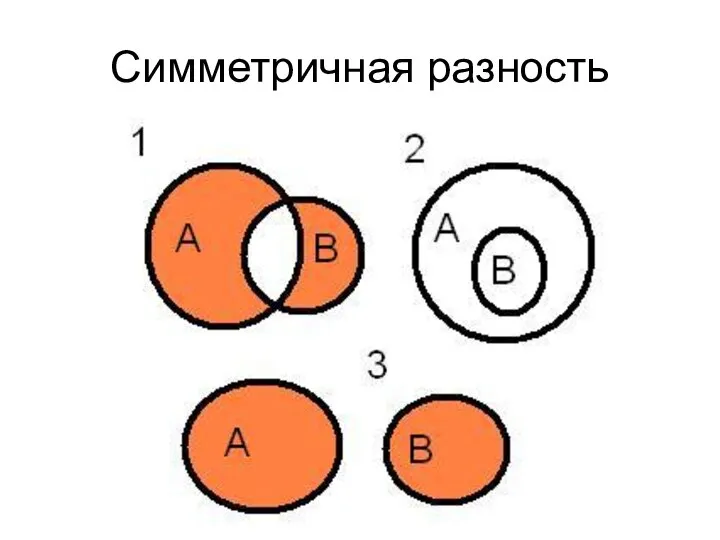
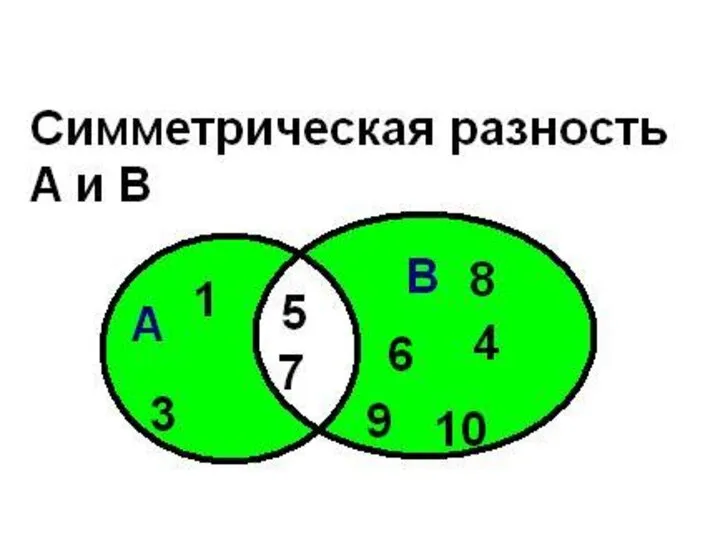
- 46. Операции над множествами Симметрической разностью множеств А и В называется множество А Δ В, являющееся объединением
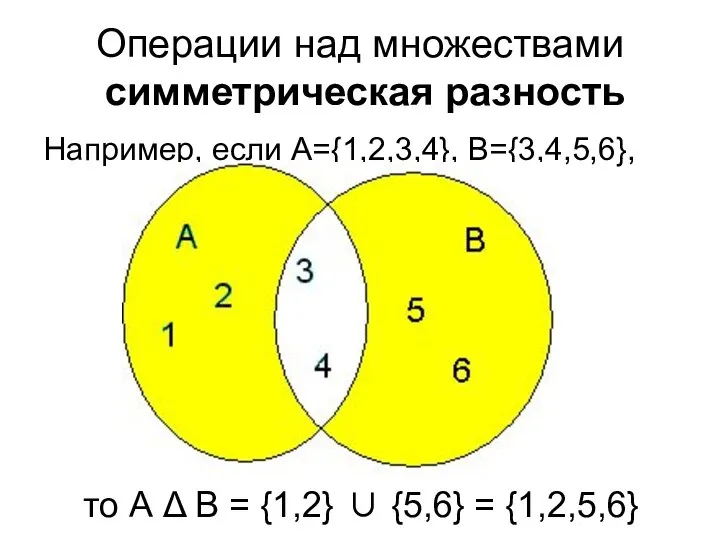
- 47. Операции над множествами симметрическая разность Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪
- 48. Симметричная разность
- 49. Операции над множествами Абсолютным дополнением множества называется множество всех элементов, не принадлежащих A, т.е. множество U\A,
- 50. Свойства операций над множествами:
- 51. П р и м е р ы Множество детей является подмножеством всего населения. Пересечением множества целых
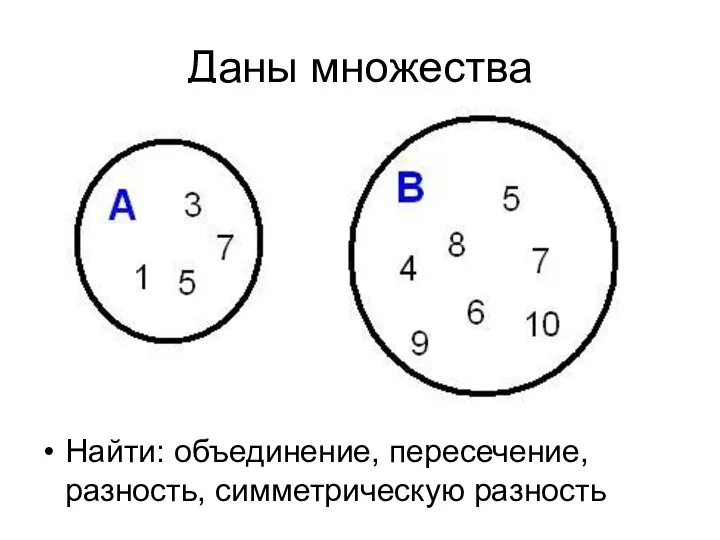
- 52. Даны множества Найти: объединение, пересечение, разность, симметрическую разность
- 58. Пример1: На вступительном экзамене по математике были предложены три задачи: по алгебре, планиметрии и стереометрии. Из
- 60. Скачать презентацию































 Учитель математики МОУ «СОШ №12» Мариничева И.М. 5класс
Учитель математики МОУ «СОШ №12» Мариничева И.М. 5класс  С 6
С 6  Событие, вероятность события. Сложение и умножение вероятностей. Понятие о независимости событий
Событие, вероятность события. Сложение и умножение вероятностей. Понятие о независимости событий Линейная алгебра
Линейная алгебра Объем фигур в пространстве
Объем фигур в пространстве Презентация по математике "Формулы сокращенного умножения 5" - скачать
Презентация по математике "Формулы сокращенного умножения 5" - скачать  Модуль Алгебра (№6-7)
Модуль Алгебра (№6-7) Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Презентация на тему Перпендикулярные прямые
Презентация на тему Перпендикулярные прямые  Построение сечений (задачи)
Построение сечений (задачи) Графики тригонометрических функций и их свойства
Графики тригонометрических функций и их свойства Геометрия. Картинки к уроку 4, М-2, часть 1
Геометрия. Картинки к уроку 4, М-2, часть 1 Задачи на доказательство № 25 из ОГЭ (геометрия)
Задачи на доказательство № 25 из ОГЭ (геометрия) Тест по теме: Координаты точки и координаты вектора
Тест по теме: Координаты точки и координаты вектора Иррациональные уравнения. Задания для устного счета
Иррациональные уравнения. Задания для устного счета Обыкновенные дроби. Урок-мозаика
Обыкновенные дроби. Урок-мозаика Аттестационная работа. Эссе о включении учащихся в проектную деятельность на уроках математики
Аттестационная работа. Эссе о включении учащихся в проектную деятельность на уроках математики Своя игра «Отношения и пропорция»
Своя игра «Отношения и пропорция» ВКОШП-2011. Разбор задач
ВКОШП-2011. Разбор задач Странички для любознательных. Что узнали. Чему научились. 2 класс
Странички для любознательных. Что узнали. Чему научились. 2 класс Цветовые схемы для мышления
Цветовые схемы для мышления Второй признак равенства треугольников
Второй признак равенства треугольников Площади многоугольников
Площади многоугольников Открытый интенсив по математике. Как мощно подготовиться к экзамену. День 1
Открытый интенсив по математике. Как мощно подготовиться к экзамену. День 1 Случайные величины. Определение случайной величины (лекция 6)
Случайные величины. Определение случайной величины (лекция 6) Кто хочет стать отличником
Кто хочет стать отличником Решение тригонометрических неравенств.10 класс ( профиль)
Решение тригонометрических неравенств.10 класс ( профиль) Прямоугольная система координат на плоскости 6 класс - презентация__________________________________________________________________________________________________________________
Прямоугольная система координат на плоскости 6 класс - презентация__________________________________________________________________________________________________________________