Содержание
- 2. Неопределенность выбора элементов хi при создании сообщения удобно характеризовать энтропией источника H(x). При независимых элементах: При
- 3. Решение: Согласно тому, как понимается здесь слово «погода» имела место 15 июля и 15 ноября, характеризуется
- 4. Поэтому погоду 15 ноября в рассматриваемом пункте следует считать более неопределенной, чем 15 июня. 1) Поэтому
- 5. Решение: 1) Строим функциональную зависимость величины энтропии от вероятности Р: Задача №2 На выходе двоичного источника
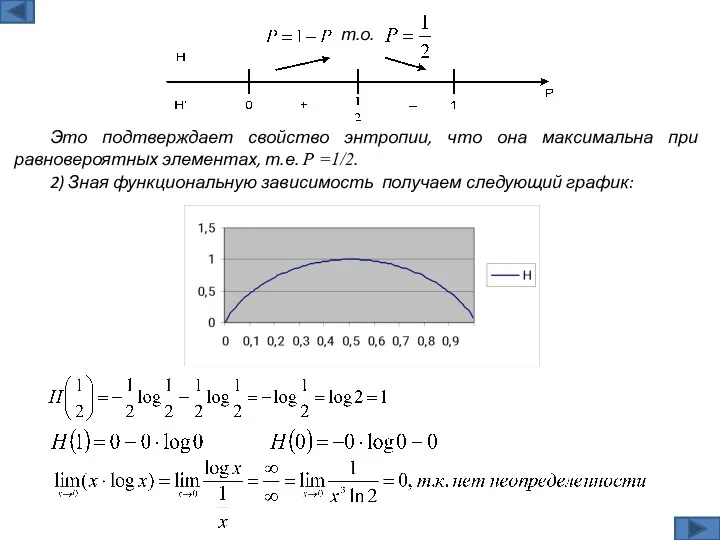
- 6. Это подтверждает свойство энтропии, что она максимальна при равновероятных элементах, т.е. Р =1/2. т.о. 2) Зная
- 7. Решение: Задача №3 Имеются два дискретных троичных источника с независимыми элементами. На выходе каждого источника появляются
- 8. Решение: Задача №4 Пусть опыты α и β состоят в последовательном извлечении двух шаров из урны,
- 9. Таким образом, безусловная энтропия опыта β равна безусловной энтропии опыта α. можно определить безусловные вероятности опыта
- 10. Решение: Полагаем, что варианты поражения целей соответствуют случайному опыту В, а выбор ракетной установки – опыту
- 11. Теперь мы можем найти условные вероятности (см. тему «условные вероятности»): В результате находим: Неопределенность ситуации, если
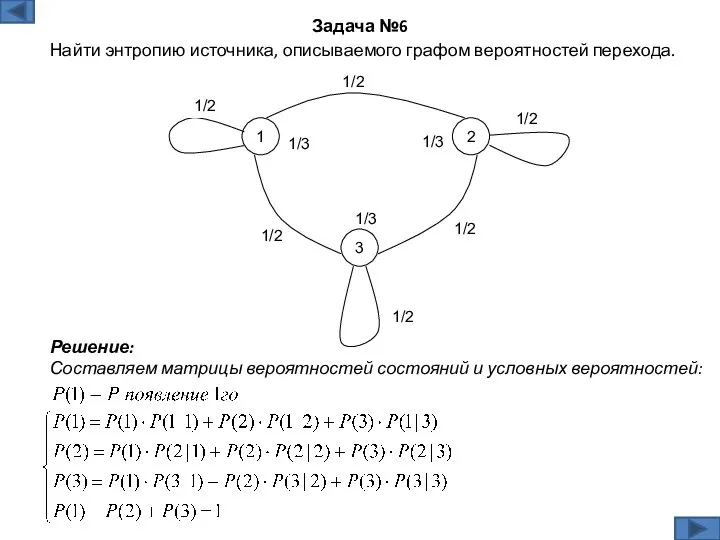
- 12. Решение: Составляем матрицы вероятностей состояний и условных вероятностей: Задача №6 Найти энтропию источника, описываемого графом вероятностей
- 13. Теперь находим среднюю условную энтропию:
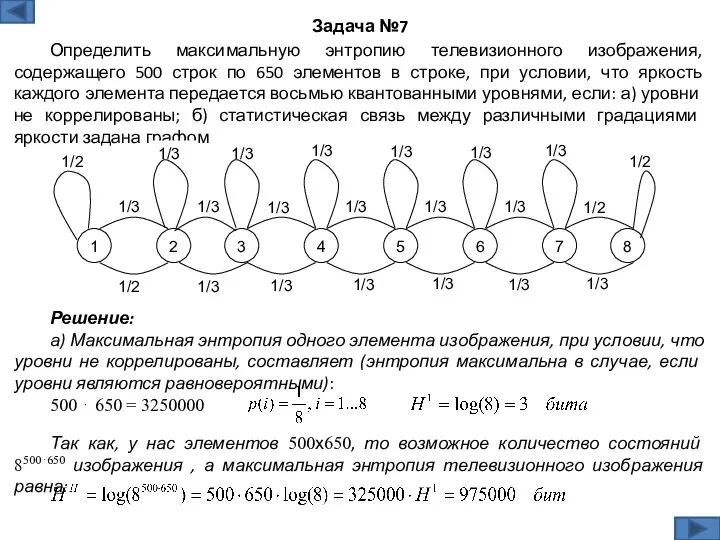
- 14. Решение: а) Максимальная энтропия одного элемента изображения, при условии, что уровни не коррелированы, составляет (энтропия максимальна
- 15. Уровни считаем равновероятными, так как ищем максимальную энтропию, значит: б) Найдем максимальную среднюю условную энтропию одного
- 16. Решение: Задача №8 Дана матрица вероятностей совместных событий: 1) Определить энтропии: H(x), H(y), Hy1(x), Hx2 (y),
- 17. 3) 4)
- 18. Решение: Так как точность измерений составляет ΔF=2кГц, то мы имеем дело с Задача №9 Информация передается
- 19. Дан сигнал с распределением f(x), который затем был квантован с точностью 1В. Известно, что появление уровней
- 20. Теперь мы можем найти энтропию данного сигнала Hx(x) :
- 21. Решение: Т.к.: H(X, Y) = H(X) + H(Y | X) и H(X, Y) = H(Y) +
- 22. Решение: Рассмотрим каждый самолет, как случайную величину. Так, как в первом случае имеет место равномерное распределение
- 23. Решение: 1) В случае равновероятных элементов большей неопределенностью обладает троичный источник. При этом неопределенность может быть
- 24. Решение: Задача №14 Определить среднюю неопределенность появления одного символа сообщения 01001000101001, при условии, что вероятность появления
- 25. Задача №16 Опыт Х – случайный выбор целого числа от 1 до 1050. Опыт Y –
- 27. Скачать презентацию





















 Презентация по математике "Сумма и произведение. Знак умножения" - скачать бесплатно
Презентация по математике "Сумма и произведение. Знак умножения" - скачать бесплатно Первый урок алгебры в 7 классе
Первый урок алгебры в 7 классе Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Треугольник и его виды
Треугольник и его виды Классическое определение вероятности события
Классическое определение вероятности события Решение простейших задач по теории вероятности
Решение простейших задач по теории вероятности Развитие понятия числа
Развитие понятия числа Презентация по математике "Дециметр" - скачать бесплатно
Презентация по математике "Дециметр" - скачать бесплатно Теория информационных процессов и систем. Лекция 1. Информационный процесс
Теория информационных процессов и систем. Лекция 1. Информационный процесс Решение уравнения с модулем
Решение уравнения с модулем Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Виды треугольников 3 класс - Презентация по математике_
Виды треугольников 3 класс - Презентация по математике_ Сечение шара плоскостью
Сечение шара плоскостью Готовимся к ОГЭ по математике, решение задания №24
Готовимся к ОГЭ по математике, решение задания №24 Тест по математике
Тест по математике Арифметическая прогрессия
Арифметическая прогрессия Простые числа
Простые числа Графики и диаграммы
Графики и диаграммы Умножение десятичных дробей
Умножение десятичных дробей Общие приемы решения олимпиадных задач
Общие приемы решения олимпиадных задач Тригонометрические уравнения Практикум по решению и составлению тригонометрических уравнений
Тригонометрические уравнения Практикум по решению и составлению тригонометрических уравнений Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями Деление обыкновенных дробей. 6 класс
Деление обыкновенных дробей. 6 класс Понятие много-один
Понятие много-один Relational algebra. Lecture 8
Relational algebra. Lecture 8 Десятичнвя дробь в виде смешанного числа
Десятичнвя дробь в виде смешанного числа Оптимизация. Математическая модель
Оптимизация. Математическая модель Параллельность в пространстве
Параллельность в пространстве