Содержание
- 2. Содержание Определение производной 3 Физический смысл производной 5 Геометрический смысл производной 9 Уравнение касательной 15 Связь
- 3. Определение Производной функции в данной точке называется предел отношения приращения функции к приращению аргумента при условии
- 5. Физический смысл производной Если материальная точка движется по закону S (t), то скорость её движения V
- 6. Задачи на физический смысл производной №1 Тело движется по прямой так, что расстояние от начальной точки
- 7. №2 Тело движется по прямой так, что расстояние от начальной точки изменяется по закону S =
- 8. Решение задач №1 V(t) = S‘(t) = 5+0,6t²; V(5) = 5+0,6*5² = 20 (м/с) №2 V(t)
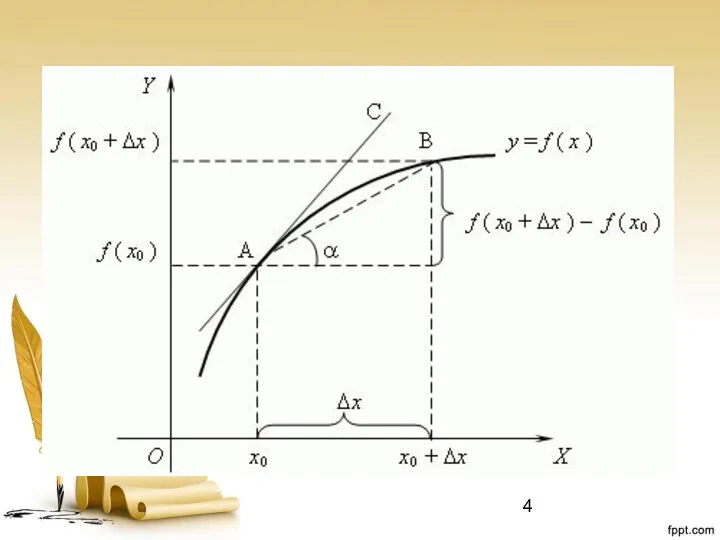
- 9. Геометрический смысл производной Геометрический смысл производной состоит в том, что значение производной функции y = f
- 10. Задачи на угловой коэффициент касательной №1 Дана функция f (x) =3x²+5x-6. Найдите координаты точки её графика,
- 11. Решение задач №1 Ккас = f ‘(x) = 6x + 5; По условию Ккас = -7,
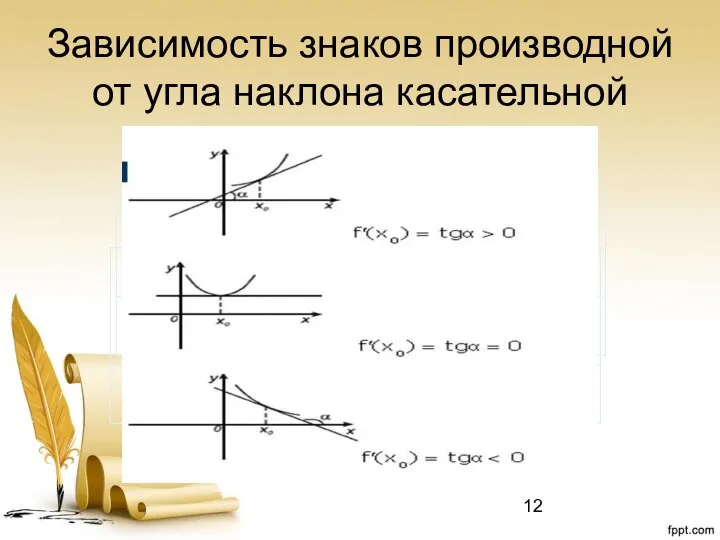
- 12. Зависимость знаков производной от угла наклона касательной
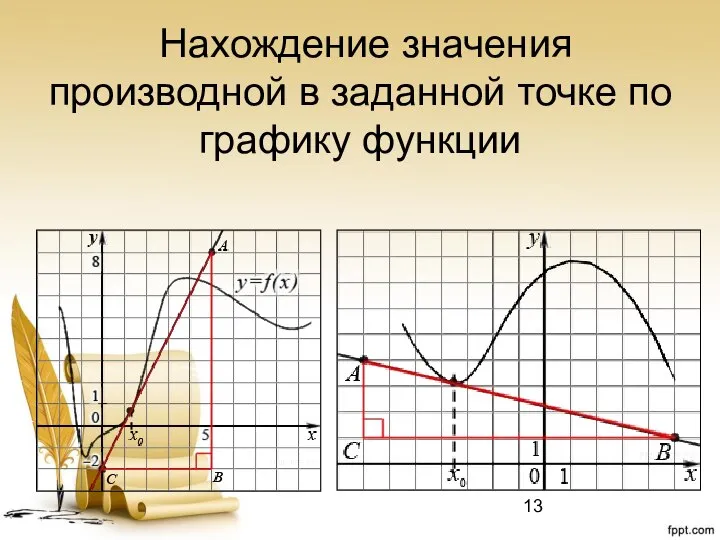
- 13. Нахождение значения производной в заданной точке по графику функции
- 14. Решение задач №1 Из ∆ ABC: tg α = tg ACB = AB/BC = 10/5 =2
- 15. Уравнение касательной дана функция y = f (x), которая имеет производную y = f ’(x) на
- 16. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке Xo
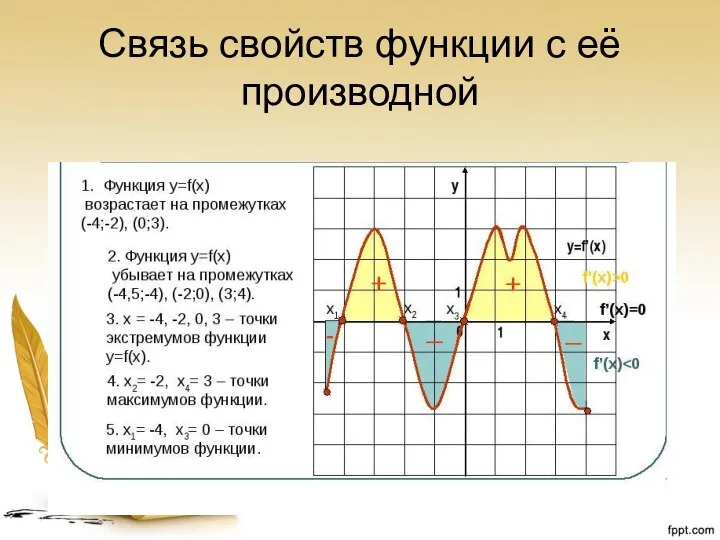
- 17. Связь свойств функции с её производной
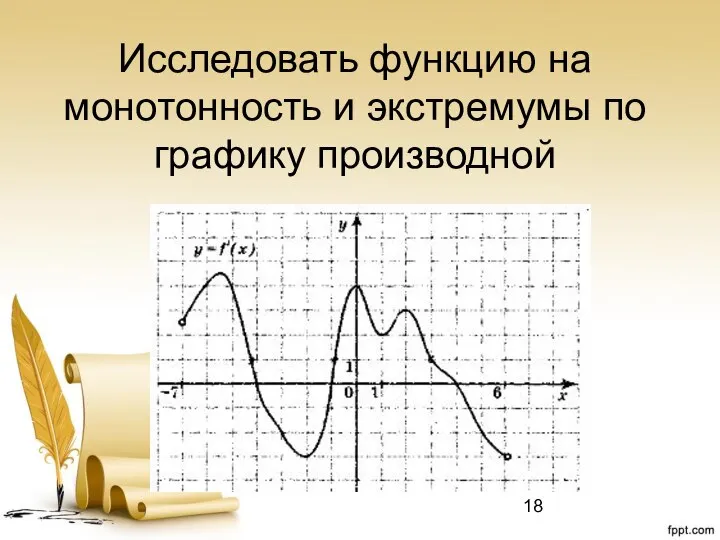
- 18. Исследовать функцию на монотонность и экстремумы по графику производной
- 20. Скачать презентацию












 Преобразование алгебраических выражений
Преобразование алгебраических выражений Задачи на смеси и сплавы
Задачи на смеси и сплавы Ряды с членами произвольного знака
Ряды с членами произвольного знака Теория надежности. Основные понятия и определения. (Лекция 1)
Теория надежности. Основные понятия и определения. (Лекция 1) Изображение точек на координатной плоскости
Изображение точек на координатной плоскости Теорема Виета. Полные, неполные и приведенные квадратные уравнения
Теорема Виета. Полные, неполные и приведенные квадратные уравнения Счёт в пределах 10
Счёт в пределах 10 Описанная окружность
Описанная окружность  Математическая статистика
Математическая статистика Математическая пицца. Игра для детей 3-7 лет
Математическая пицца. Игра для детей 3-7 лет Дія ділення.(2 клас)
Дія ділення.(2 клас) Основы стандартизации, сертификации и метрологии
Основы стандартизации, сертификации и метрологии Презентация по математике "Линейное уравнение с двумя переменными. График линейного уравнения с двумя переменными" - скачать
Презентация по математике "Линейное уравнение с двумя переменными. График линейного уравнения с двумя переменными" - скачать  Стандартизация статистических показателей
Стандартизация статистических показателей Общие сведения о формальных и аксиоматических системах
Общие сведения о формальных и аксиоматических системах Линейная функция, её график и свойства
Линейная функция, её график и свойства Сложение чисел с разными знаками. Верные равенства
Сложение чисел с разными знаками. Верные равенства Параллелепипед. Задания для устного счета. Упражнение 6
Параллелепипед. Задания для устного счета. Упражнение 6 Решение логарифмических неравенств
Решение логарифмических неравенств Математическое развитие детей в семье
Математическое развитие детей в семье Презентация по математике "Решение уравнений с использованием графической модели" - скачать
Презентация по математике "Решение уравнений с использованием графической модели" - скачать  Золотое сечение в архитектуре
Золотое сечение в архитектуре Признаки параллельности прямых. Решение задач по готовым чертежам
Признаки параллельности прямых. Решение задач по готовым чертежам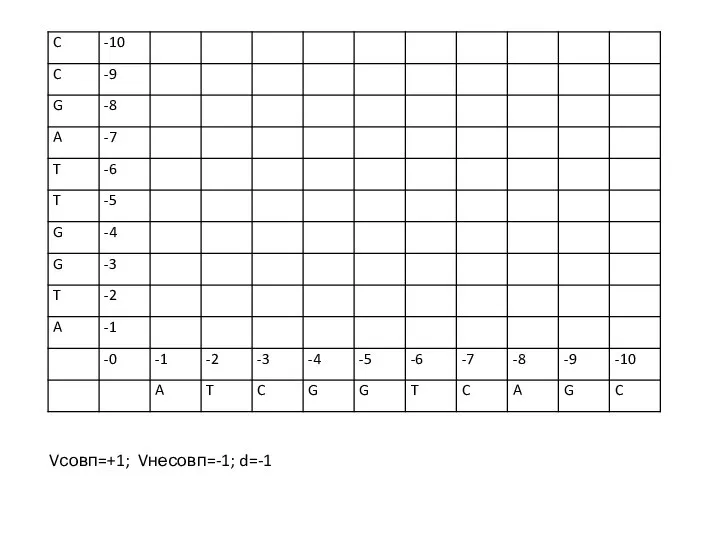 Координаты (таблица)
Координаты (таблица) Похідна складеної функції
Похідна складеної функції Решение задач в целых числах
Решение задач в целых числах Площадь криволинейной трапеции. Определенный интеграл
Площадь криволинейной трапеции. Определенный интеграл Стереометрія. Аксіоми стереометрії
Стереометрія. Аксіоми стереометрії