Содержание
- 10. График четной функции симметричен относительно оси а нечетной − относительно точки С (0;0), т.е. начала координат.
- 15. Кратко определение предела можно записать так:
- 16. Геометрический смысл определения предела последовательности: Неравенство равносильно неравенствам или т.е. Поэтому определение предела последовательности можно сформулировать
- 18. Предел функции в точке. Бесконечно большая и бесконечно малая функция.
- 26. А если условия этой теоремы не выполнены, то могут возникнуть неопределенности вида : которые в простейших
- 33. ПРОИЗВОДНАЯ ФУНКЦИИ Определение производной Геометрический смысл производной Связь между непрерывностью и дифференцируемостью Производные основных элементарных функций
- 34. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ Найдем соответствующее приращение функции:
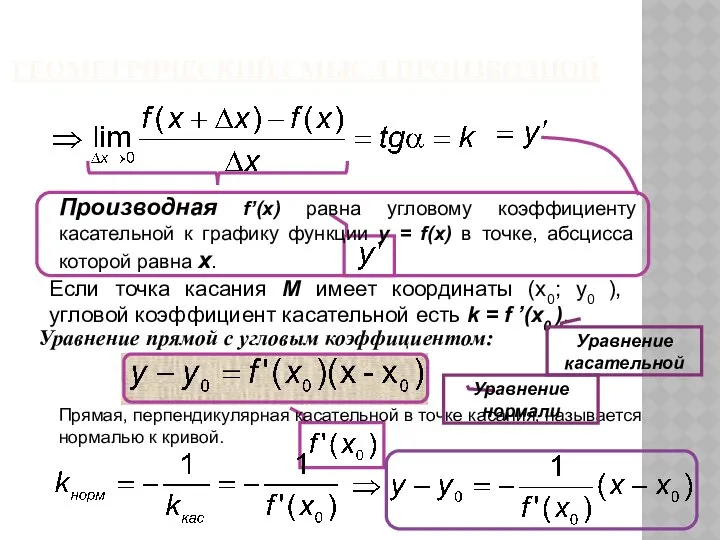
- 35. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
- 36. Если точка касания М имеет координаты (x0; y0 ), угловой коэффициент касательной есть k = f
- 37. СВЯЗЬ МЕЖДУ НЕПРЕРЫВНОСТЬЮ И ДИФФЕРЕНЦИРУЕМОСТЬЮ ФУНКЦИИ Если функция f(x) дифференцируема в некоторой точке , то она
- 38. Нахождение производной называют дифференцированием
- 39. ТАБЛИЦА ПРОИЗВОДНЫХ
- 40. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b) функции,
- 41. ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ 1. Если функции u(x) и v(x) имеют в точке х производные, то их
- 42. ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ 3. Если функции u(x) и v(x) имеют в точке х производные, то их
- 43. ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ 5. Если функции u(x) и v(x) имеют в точке х производные и v(x)
- 44. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x))
- 45. ПРИМЕР Вычислить производную функции
- 46. ПРИМЕР: Вычислить производную функции: Данную функцию можно представить следующим образом: Коротко:
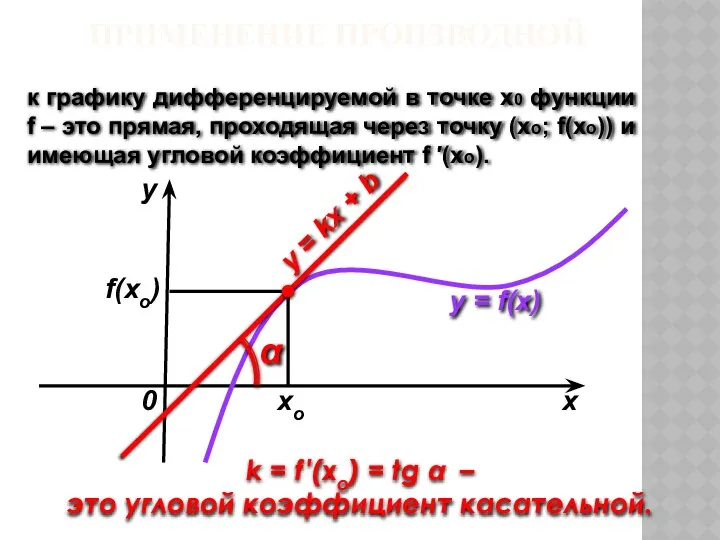
- 47. k = f ′(xo) = tg α – это угловой коэффициент касательной. Касательная к графику дифференцируемой
- 48. Общий вид уравнения касательной y = f ′(xo)(x – xo) + f(xo) Алгоритм составления уравнения касательной
- 49. Одна из основных задач исследования функции – это нахождение промежутков её возрастания и убывания. Признак возрастания
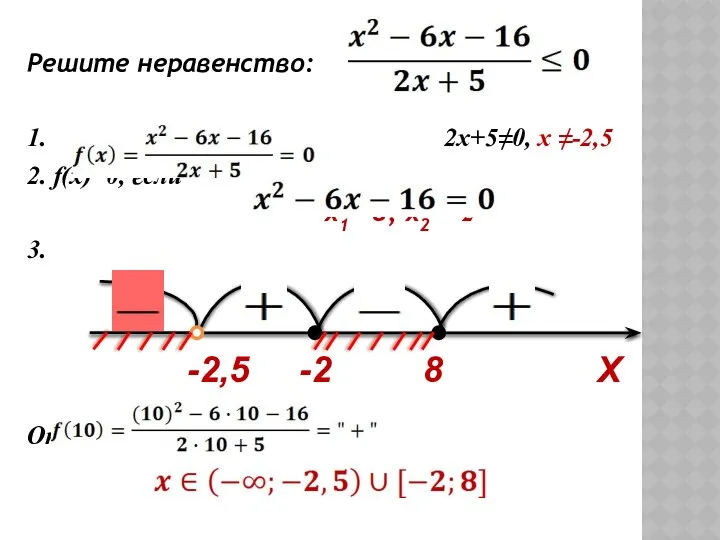
- 50. АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ: Выделить функцию y=f(x). Найти область определения функции D(f). Указать промежутки непрерывности.
- 51. Решите неравенство: 1. 2x+5≠0, х ≠-2,5 2. f(x)=0, если x1= 8, x2= -2 3. Ответ:
- 52. АЛГОРИТМ НАХОЖДЕНИЯ ПРОМЕЖУТКОВ ВОЗРАСТАНИЯ (УБЫВАНИЯ) ФУНКЦИИ y=f(x): Найти производную функции f´(x). Решить уравнение f´ (x) =0.
- 53. Найдите промежутки возрастания и убывания функции: 1. 2. f´(x)=0, если 3. Ответ:
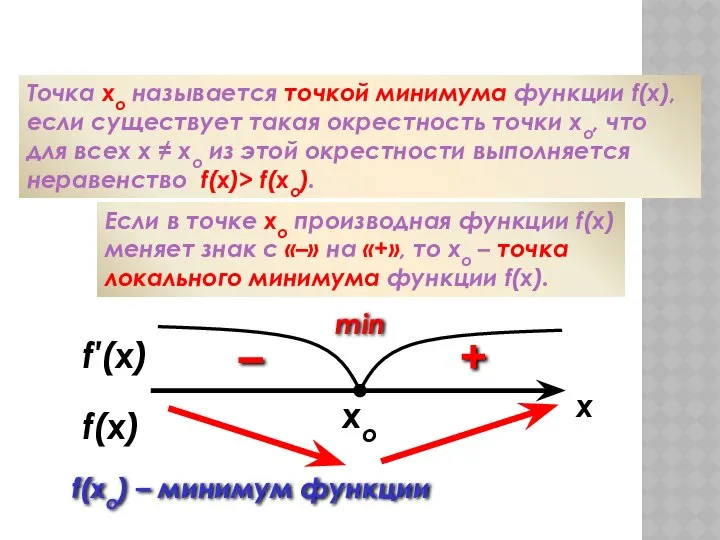
- 54. f′(x) xo Минимум функции Точка хо называется точкой минимума функции f(x), если существует такая окрестность точки
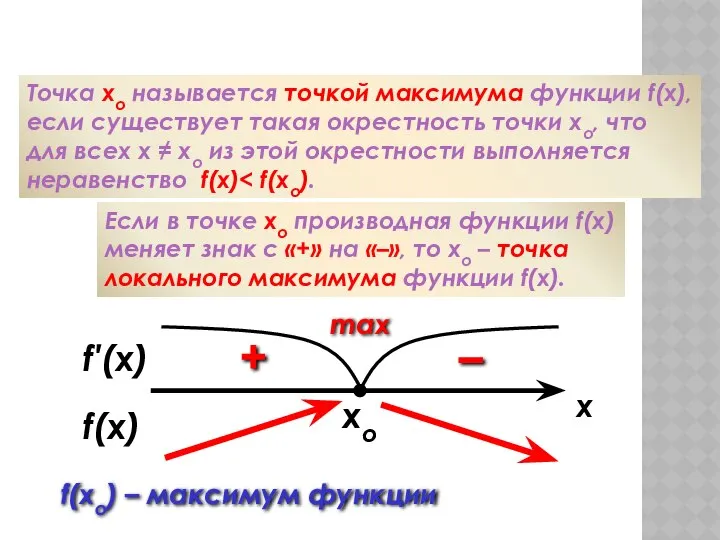
- 55. xo Максимум функции Точка хо называется точкой максимума функции f(x), если существует такая окрестность точки хо,
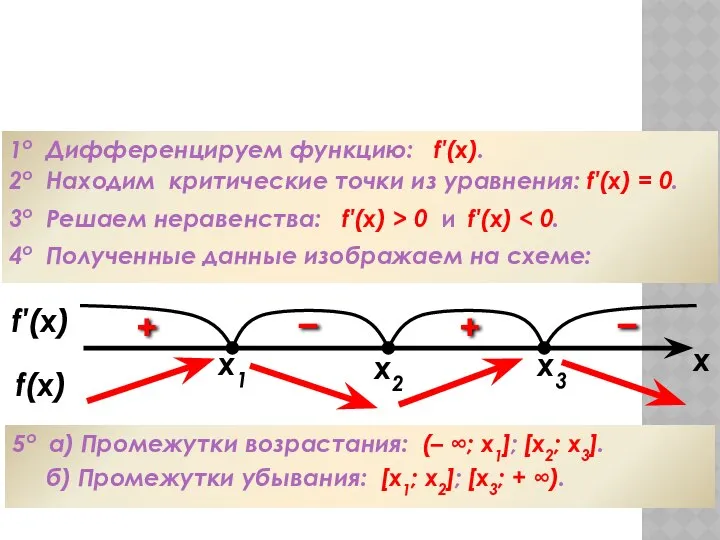
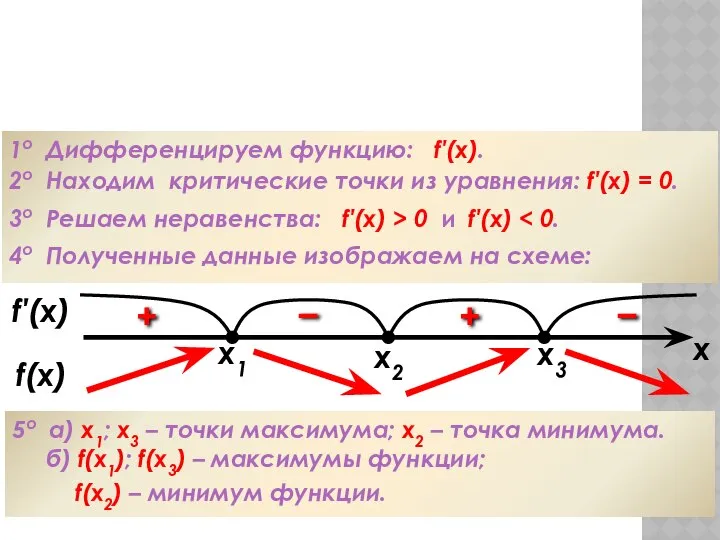
- 56. Алгоритм исследования функции на монотонность 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
- 57. Алгоритм исследования функции на экстремумы 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
- 58. ПРИМЕРЫ
- 61. Скачать презентацию





























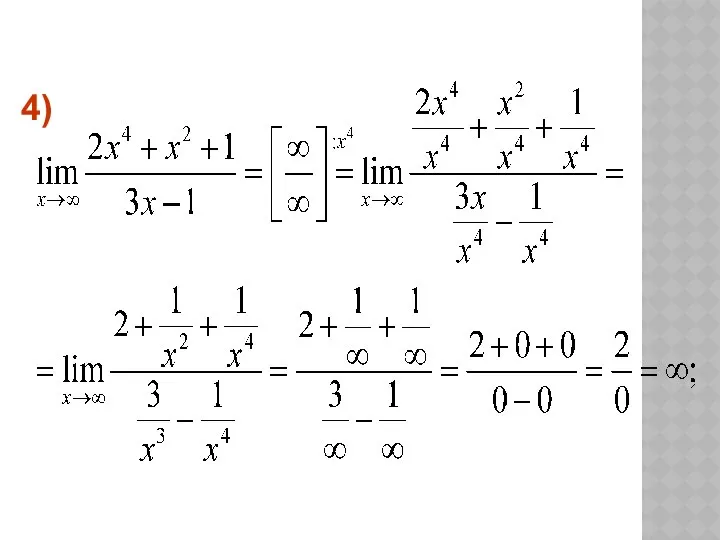






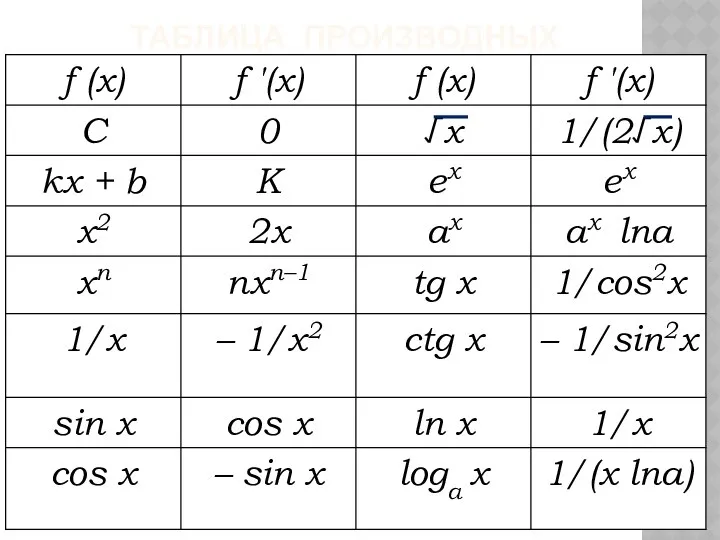













 Производная функции
Производная функции Определение угла. Развёрнутый угол
Определение угла. Развёрнутый угол Вписанная и описанная окружности
Вписанная и описанная окружности Вычисление значения функции по формуле
Вычисление значения функции по формуле Стандартный вид числа
Стандартный вид числа Сравнительный анализ
Сравнительный анализ Интерактивные тренинги по геометрии для подготовки к ОГЭ
Интерактивные тренинги по геометрии для подготовки к ОГЭ Производная функции
Производная функции Натуральные числа и дроби
Натуральные числа и дроби Презентация на тему Проценты в нашей жизни
Презентация на тему Проценты в нашей жизни Презентация по математике "Сложение и вычитание чисел" - скачать
Презентация по математике "Сложение и вычитание чисел" - скачать  Презентация по математике "Процентные вычисления и расчёты" - скачать
Презентация по математике "Процентные вычисления и расчёты" - скачать  Математика - 6. Домашнее задание
Математика - 6. Домашнее задание Преобразование графиков функций
Преобразование графиков функций Готовимся к ОГЭ по математике
Готовимся к ОГЭ по математике Координаты Подготовила и провела в 7 классе: Учитель математики и информатики Яковлева Н.С.
Координаты Подготовила и провела в 7 классе: Учитель математики и информатики Яковлева Н.С. Урок математики1 класс МОУ СОШ №128 Учитель:Лебедева Нина Ивановна Тема урока: Числа от 1 до 10. Цель урока: создать условия для закр
Урок математики1 класс МОУ СОШ №128 Учитель:Лебедева Нина Ивановна Тема урока: Числа от 1 до 10. Цель урока: создать условия для закр Уравнения, сводящиеся к квадратным
Уравнения, сводящиеся к квадратным Весёлая математика Авторы: Ульянина К., Сапожников Н., Толстова И.,Вершинин А.,Семенюта Е.
Весёлая математика Авторы: Ульянина К., Сапожников Н., Толстова И.,Вершинин А.,Семенюта Е. Презентация по математике "Решаем задачи и примеры. 2класс" - скачать
Презентация по математике "Решаем задачи и примеры. 2класс" - скачать  Куб (текше) және оның көлемі
Куб (текше) және оның көлемі Масштаб. Решение задач
Масштаб. Решение задач Сложение и вычитание обыкновенных дробей с разными знаменателями
Сложение и вычитание обыкновенных дробей с разными знаменателями Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна
Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна  Звездчатые многогранники
Звездчатые многогранники Сравнение бесконечно больших и бесконечно малых величин
Сравнение бесконечно больших и бесконечно малых величин Степень с натуральным показателем и ее свойства
Степень с натуральным показателем и ее свойства «Геометрия приближает разум к истине» Платон
«Геометрия приближает разум к истине» Платон