Содержание
- 2. 3. Основные характеристики функции Чётность функции Функция f(x) четная, если справедливо равенство График четной функции симметричен
- 3. Функция f(x) нечетная, если справедливо равенство График нечетной функции симметричен относительно начало координат (0;0)
- 4. Функция, которая не является четной или нечетной называется функцией общего вида.
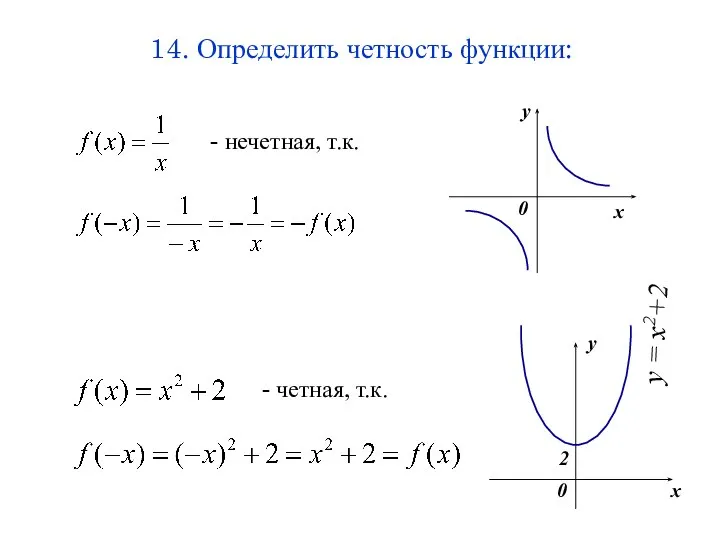
- 5. 14. Определить четность функции: 2 - нечетная, т.к. - четная, т.к.
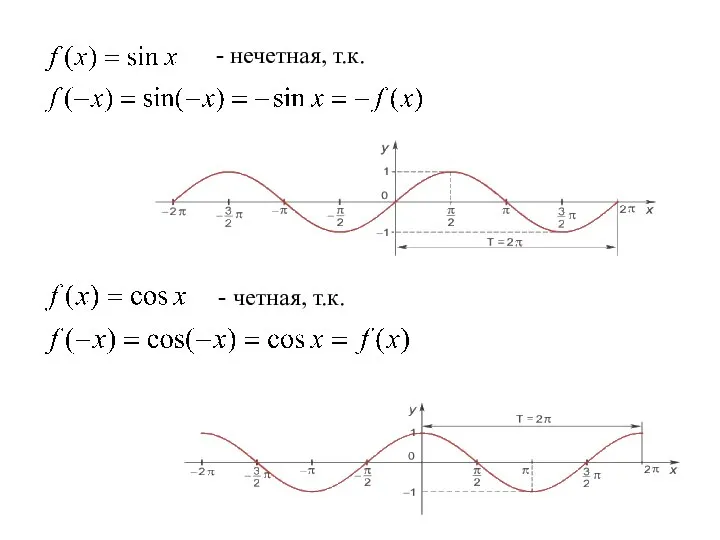
- 6. - нечетная, т.к. - четная, т.к.
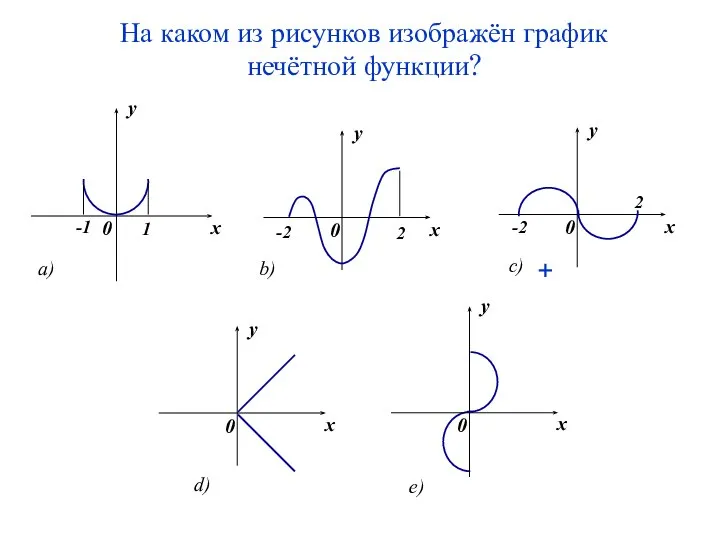
- 7. На каком из рисунков изображён график нечётной функции? +
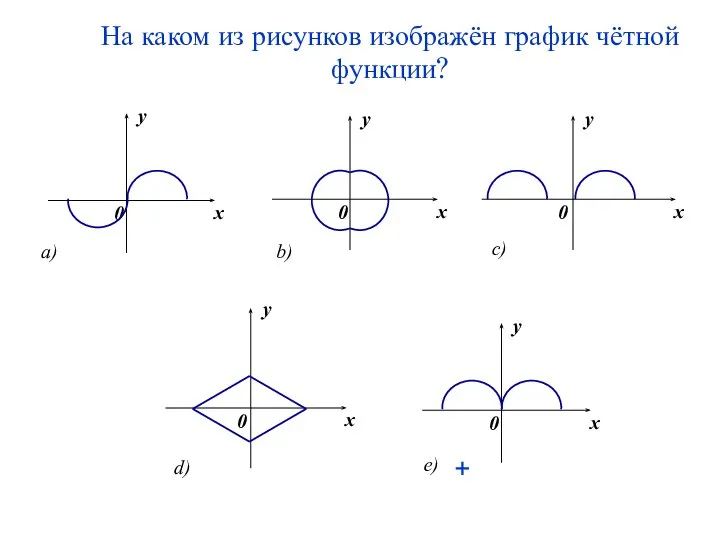
- 8. На каком из рисунков изображён график чётной функции? +
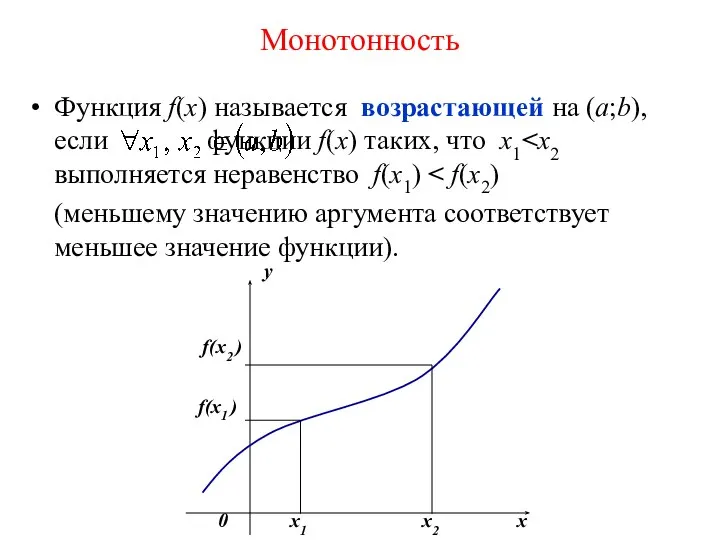
- 9. Монотонность Функция f(х) называется возрастающей на (а;b), если функции f(x) таких, что x1 (меньшему значению аргумента
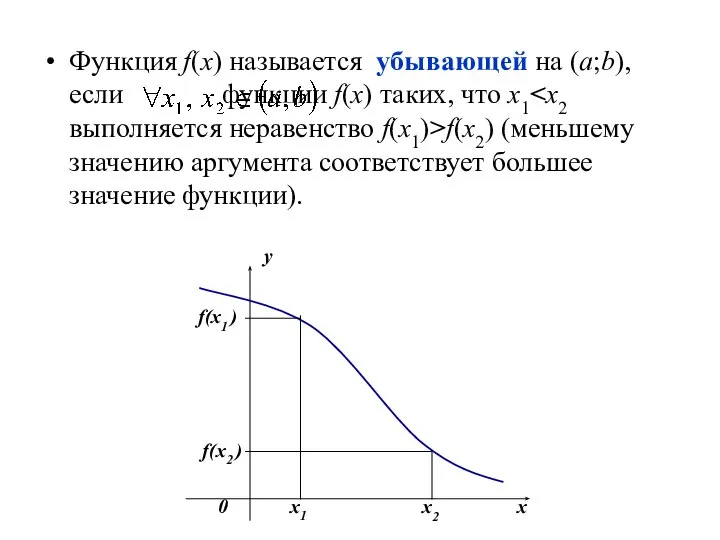
- 10. Функция f(х) называется убывающей на (а;b), если функции f(x) таких, что x1 f(x2) (меньшему значению аргумента
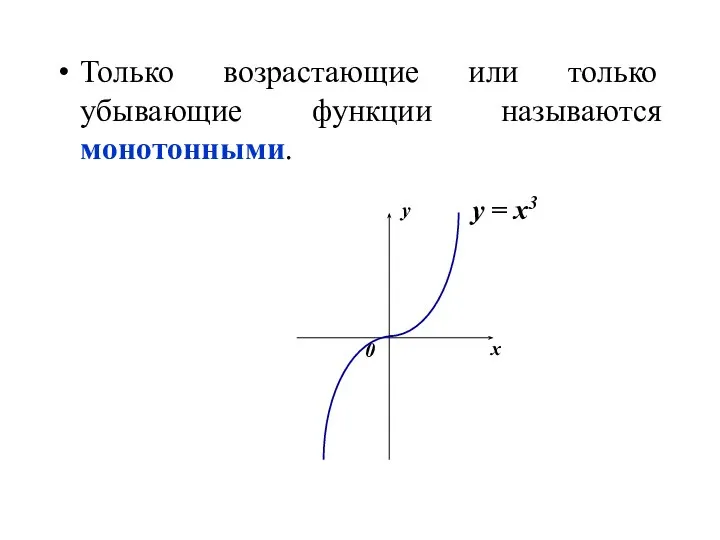
- 11. Только возрастающие или только убывающие функции называются монотонными.
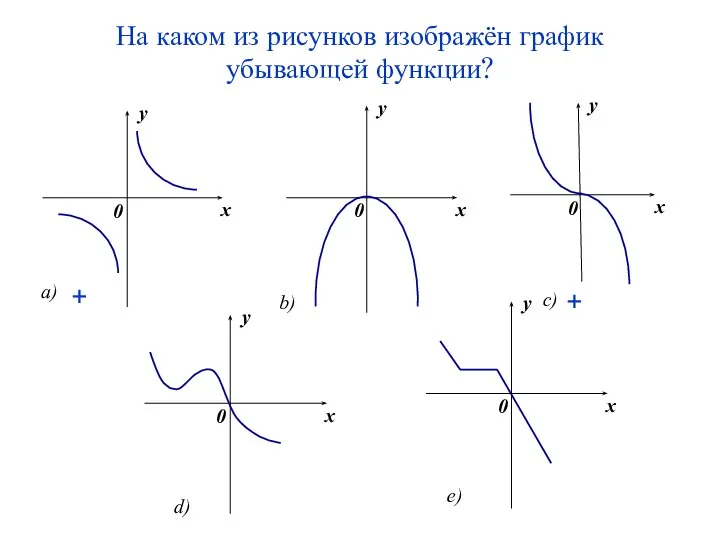
- 12. На каком из рисунков изображён график убывающей функции? + +
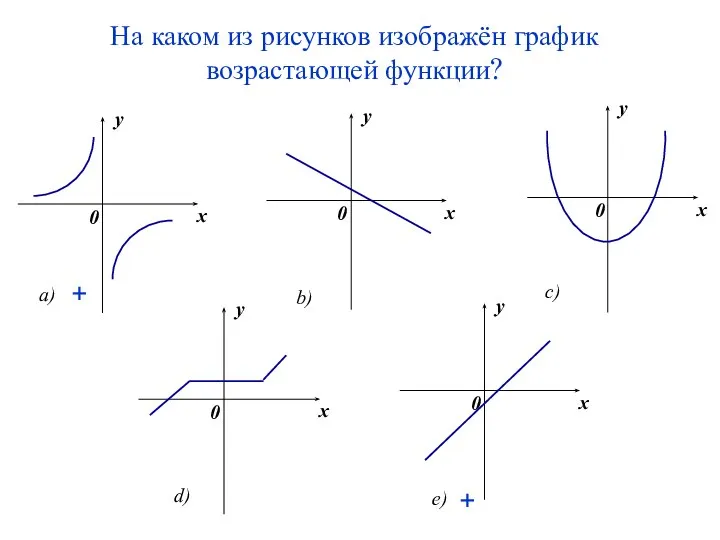
- 13. На каком из рисунков изображён график возрастающей функции? + +
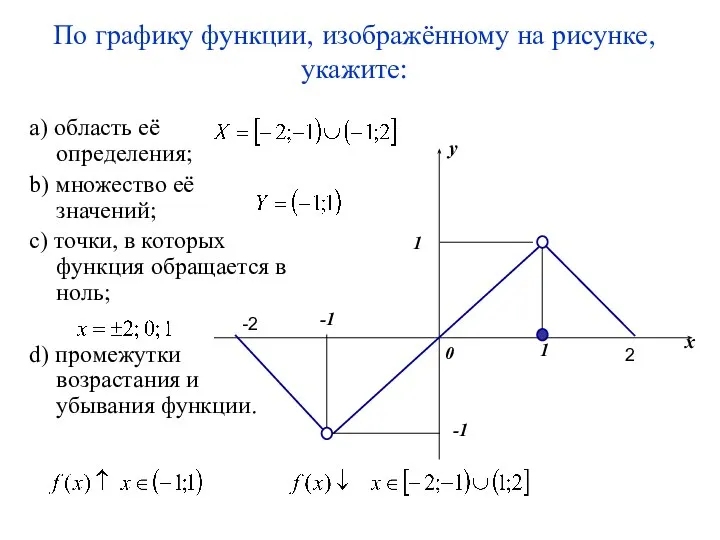
- 14. По графику функции, изображённому на рисунке, укажите: a) область её определения; b) множество её значений; c)
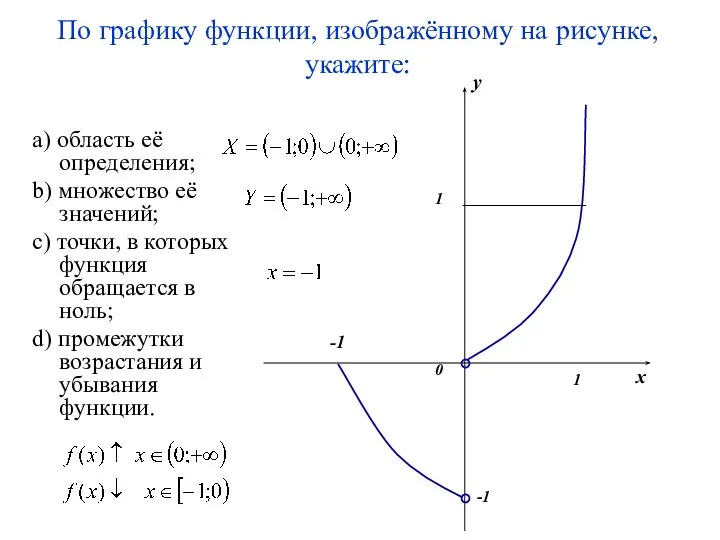
- 15. По графику функции, изображённому на рисунке, укажите: a) область её определения; b) множество её значений; c)
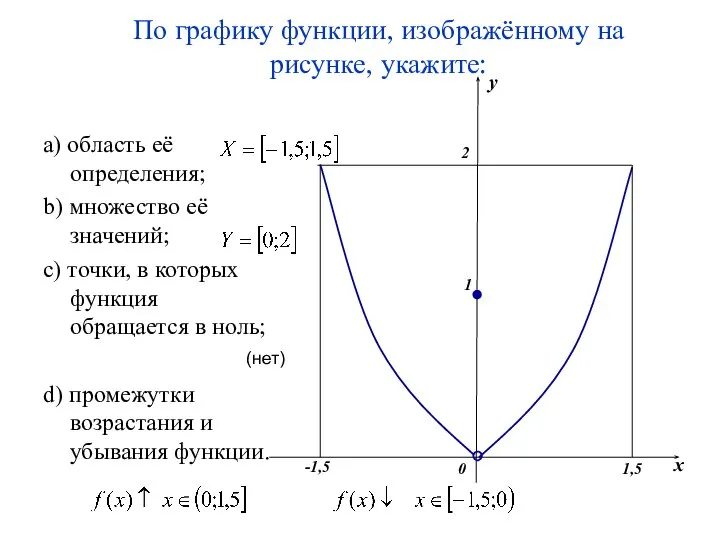
- 16. По графику функции, изображённому на рисунке, укажите: a) область её определения; b) множество её значений; c)
- 17. По графику функции, изображённому на рисунке, укажите: a) область её определения; b) множество её значений; c)
- 18. Функция f(x) называется периодической, если существует такое число Т≠0 (называемое периодом), что в каждой точке области
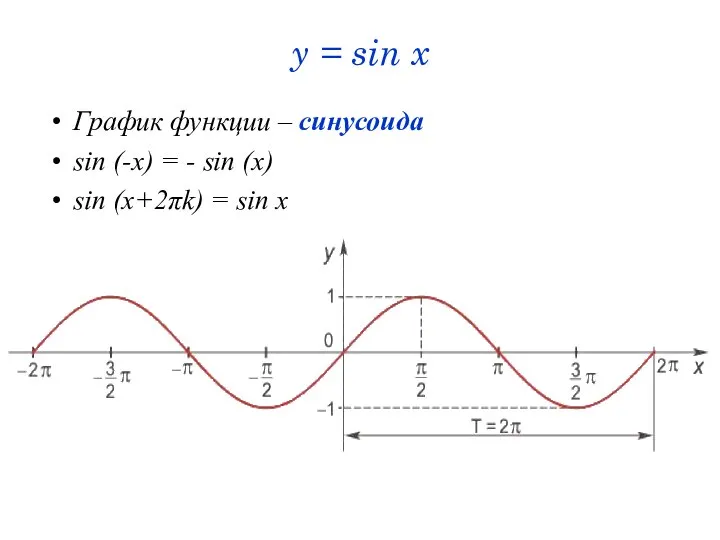
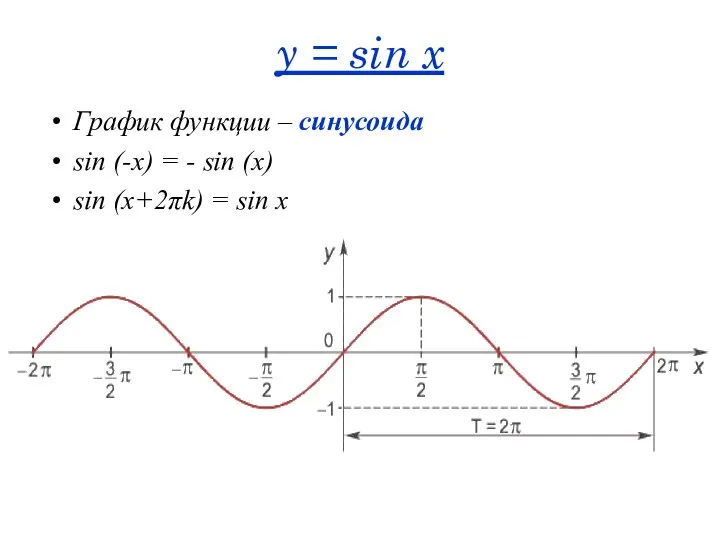
- 19. y = sin x График функции – синусоида sin (-x) = - sin (x) sin (x+2πk)
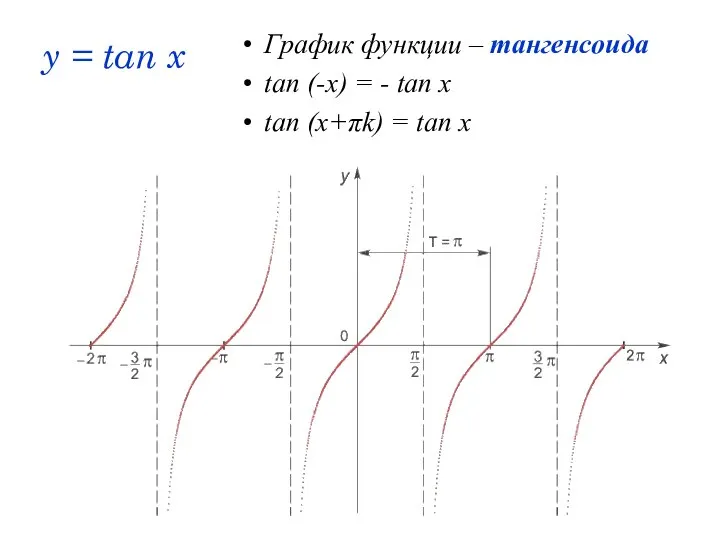
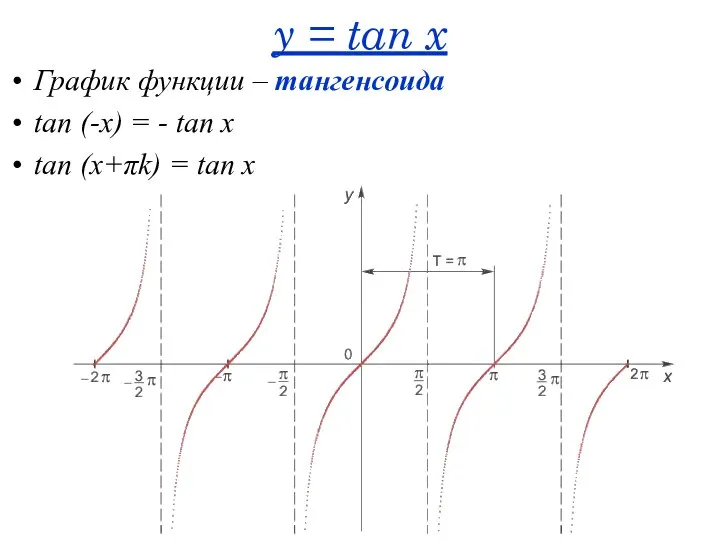
- 20. y = tan x График функции – тангенсоида tan (-x) = - tan x tan (x+πk)
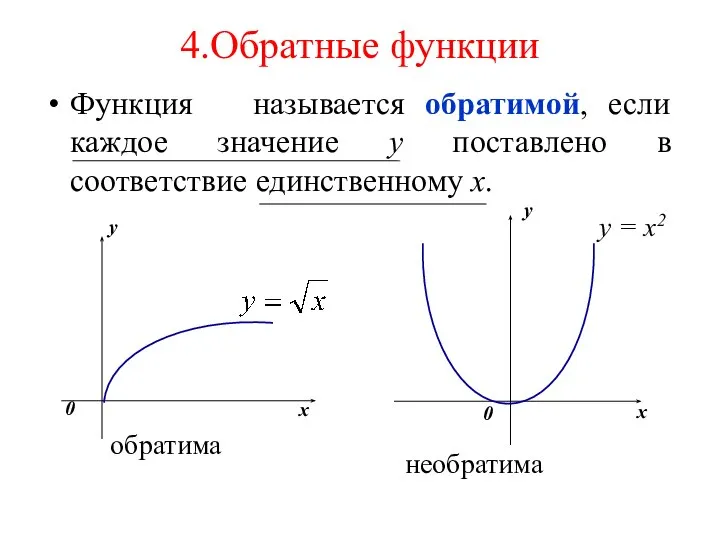
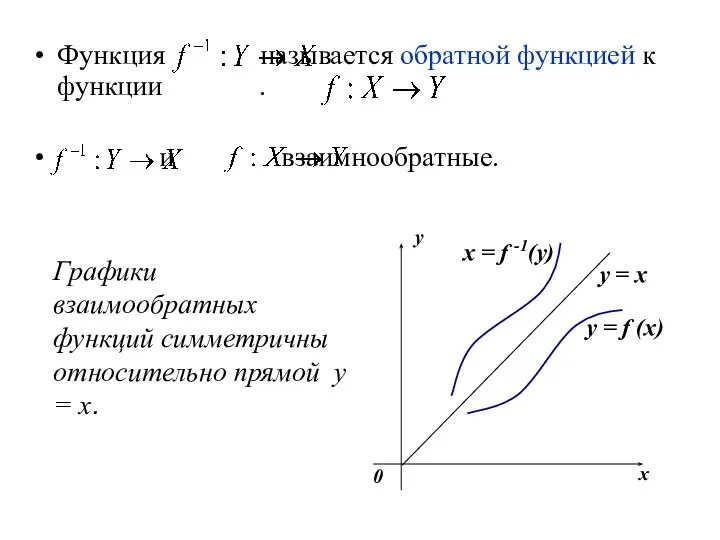
- 21. 4.Обратные функции Функция называется обратимой, если каждое значение у поставлено в соответствие единственному х.
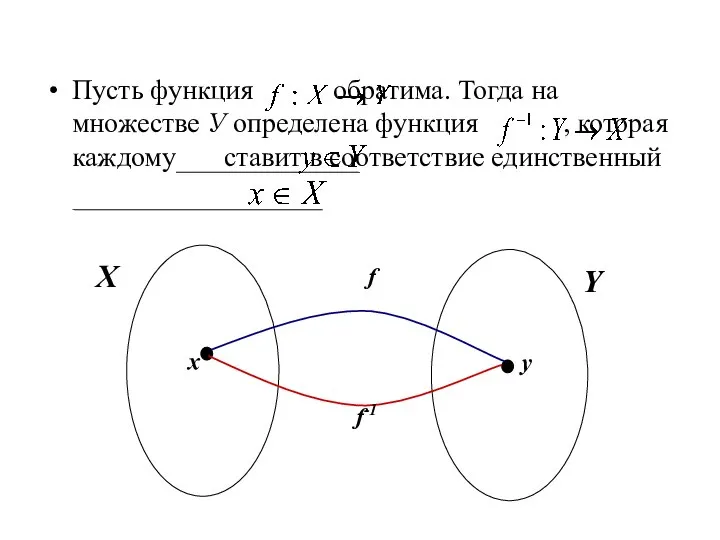
- 22. Пусть функция обратима. Тогда на множестве У определена функция , которая каждому ставит в соответствие единственный
- 23. Функция называется обратной функцией к функции . и взаимнообратные. Графики взаимообратных функций симметричны относительно прямой у
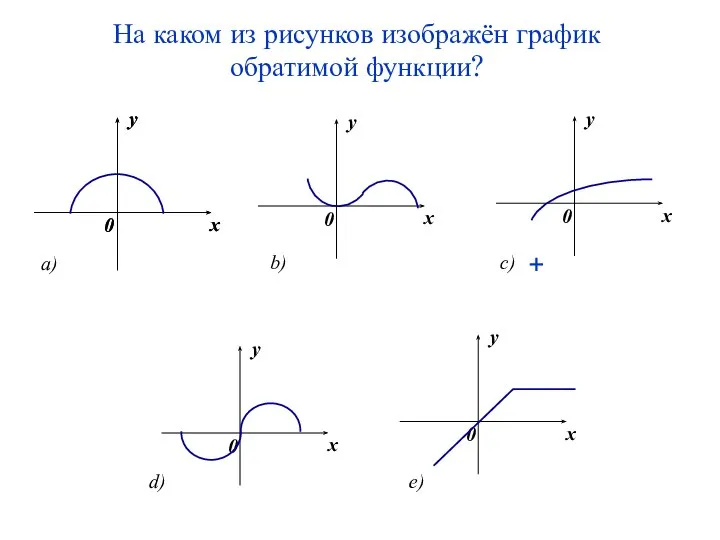
- 24. На каком из рисунков изображён график обратимой функции? +
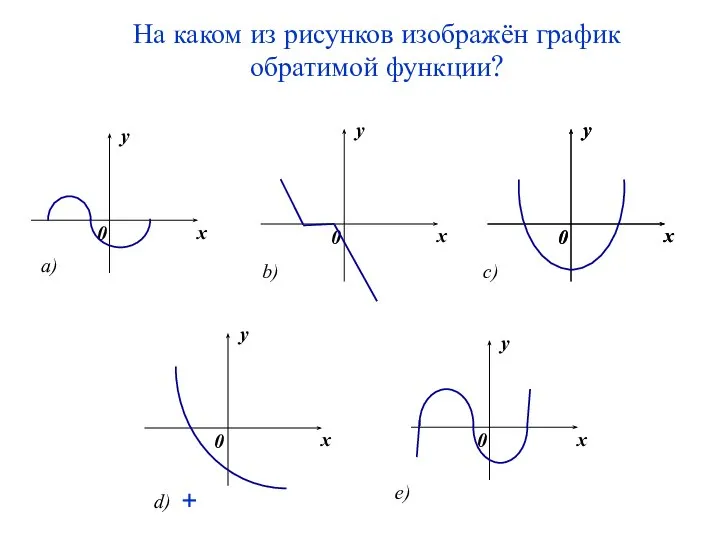
- 25. На каком из рисунков изображён график обратимой функции? +
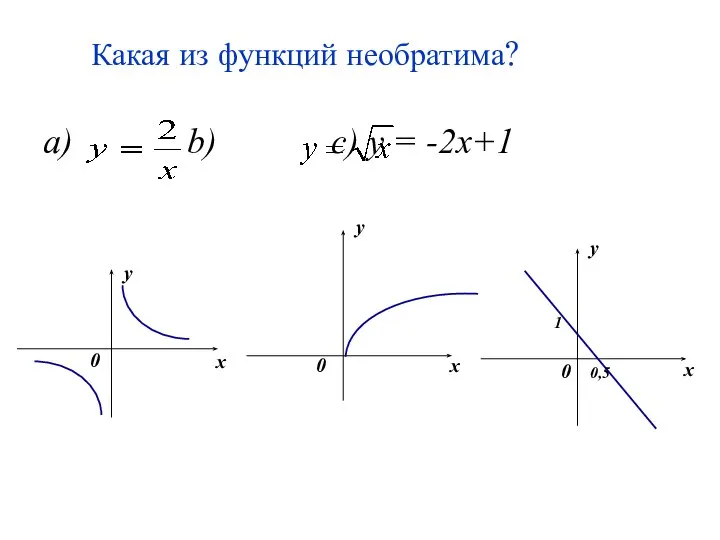
- 26. Какая из функций необратима? a) b) c) y = -2x+1
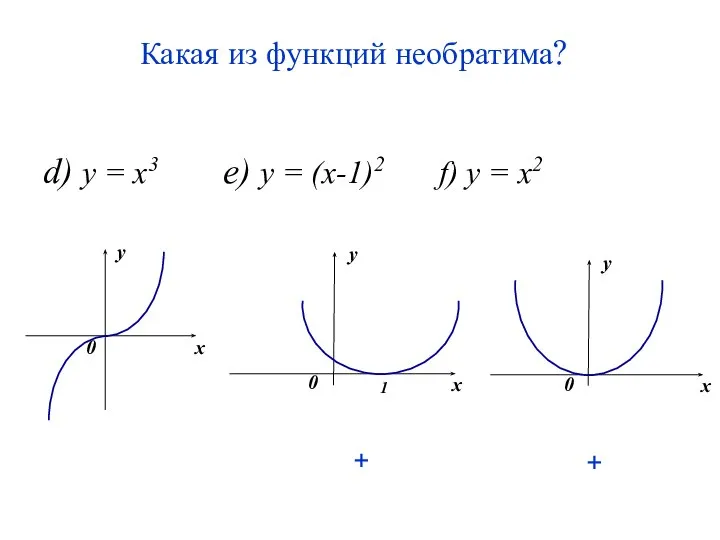
- 27. Какая из функций необратима? d) y = x3 e) y = (x-1)2 f) y = x2
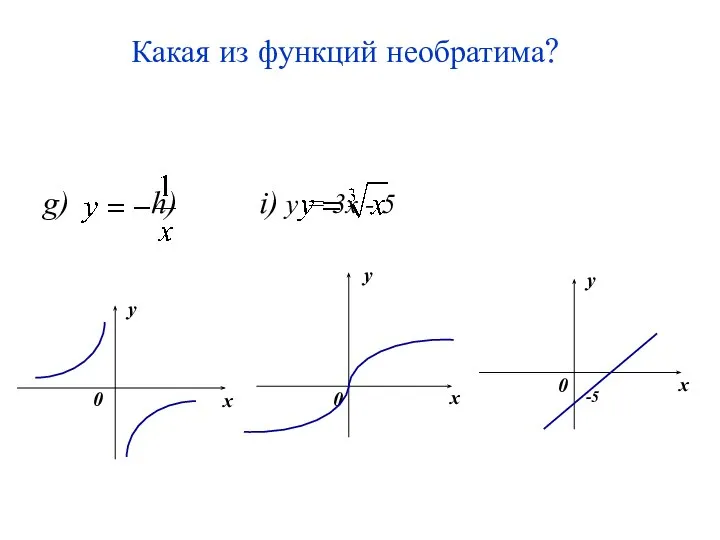
- 28. Какая из функций необратима? g) h) i) y = 3x - 5
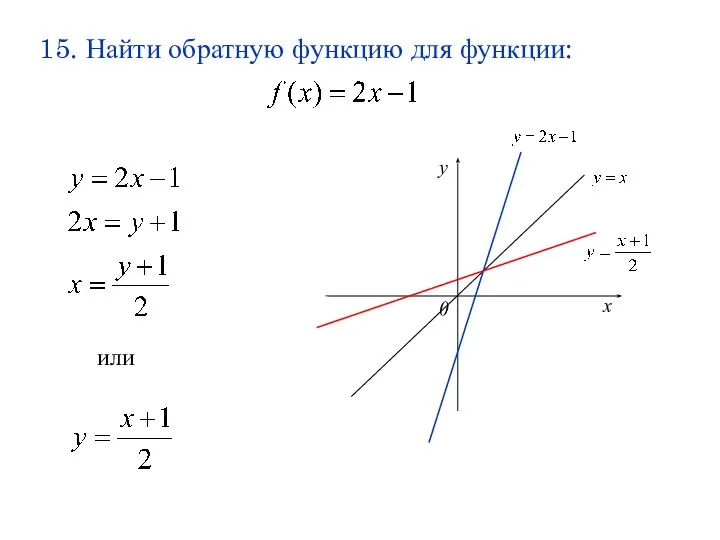
- 29. 15. Найти обратную функцию для функции: или х у 0
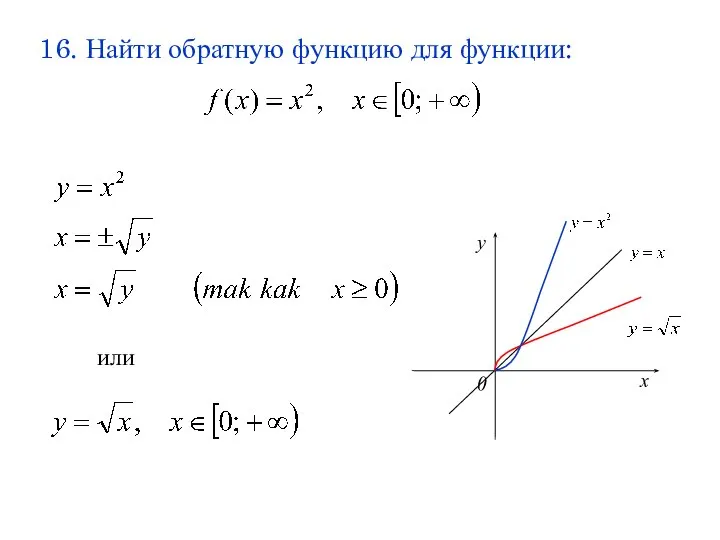
- 30. 16. Найти обратную функцию для функции: или х у 0
- 31. 5. Основные элементарные функции Степенная функция. Показательная функция Логарифмическая функция Тригонометрические функции Обратные тригонометрические функции
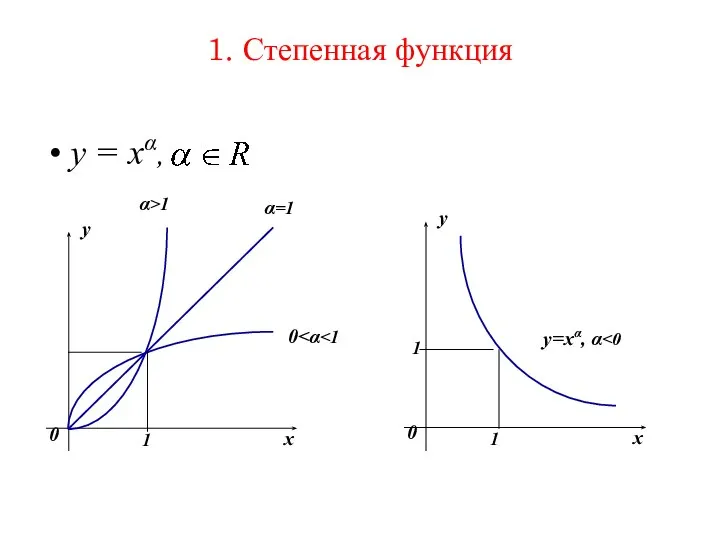
- 32. 1. Степенная функция y = xα,
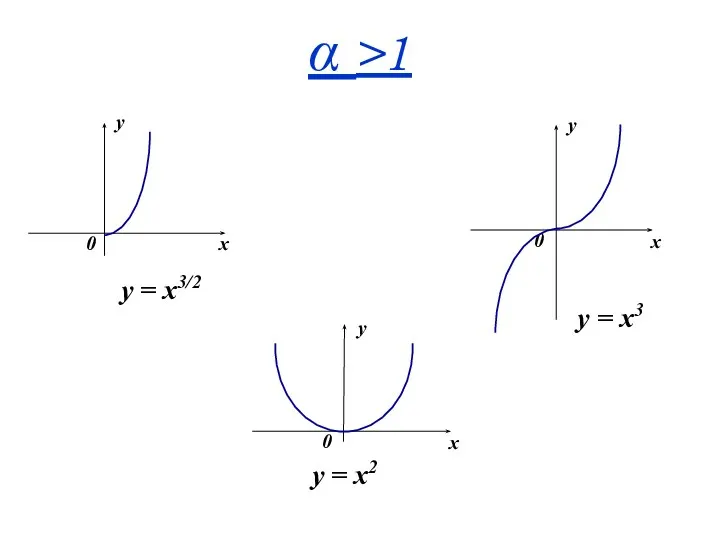
- 33. α >1
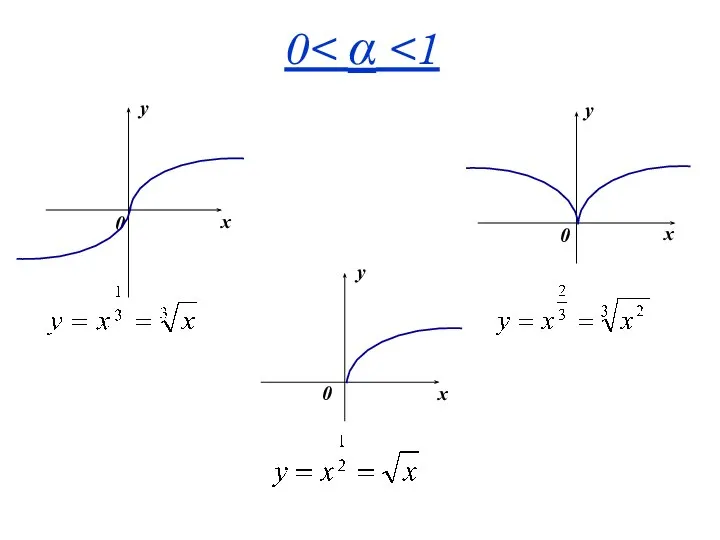
- 34. 0
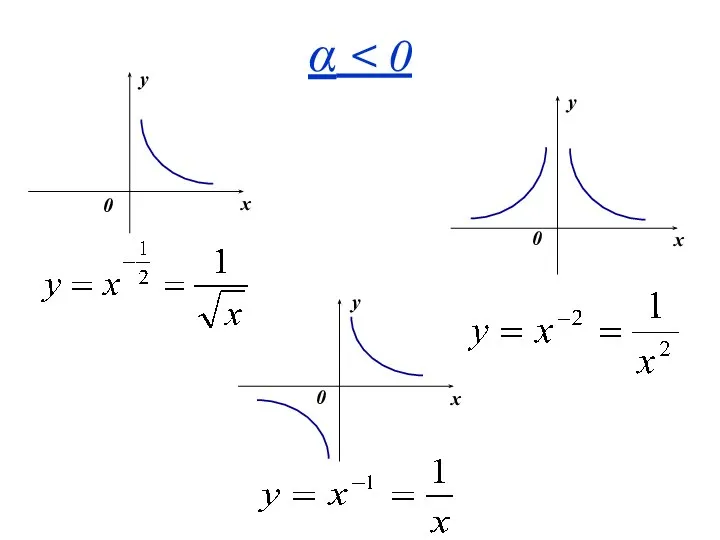
- 35. α
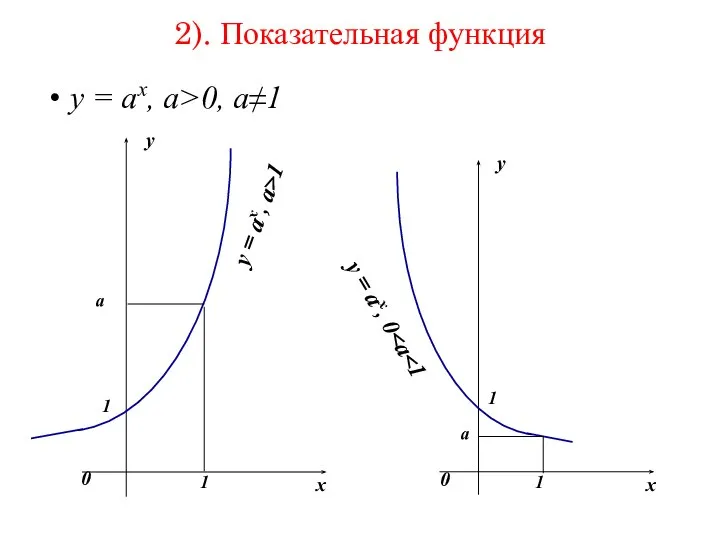
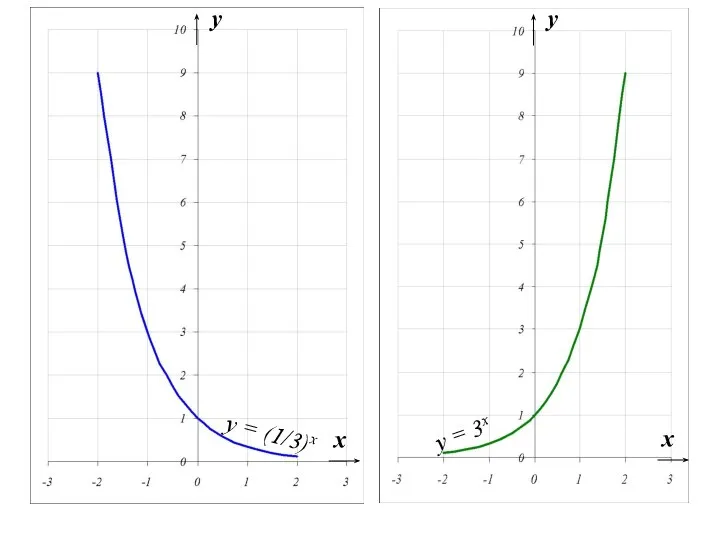
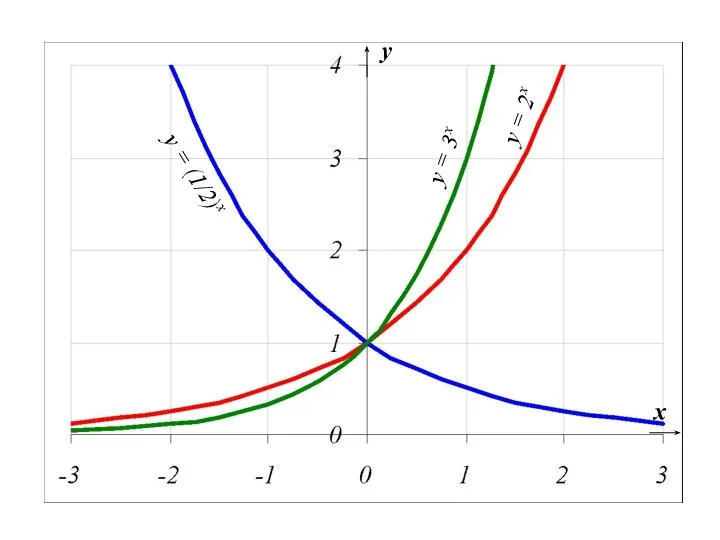
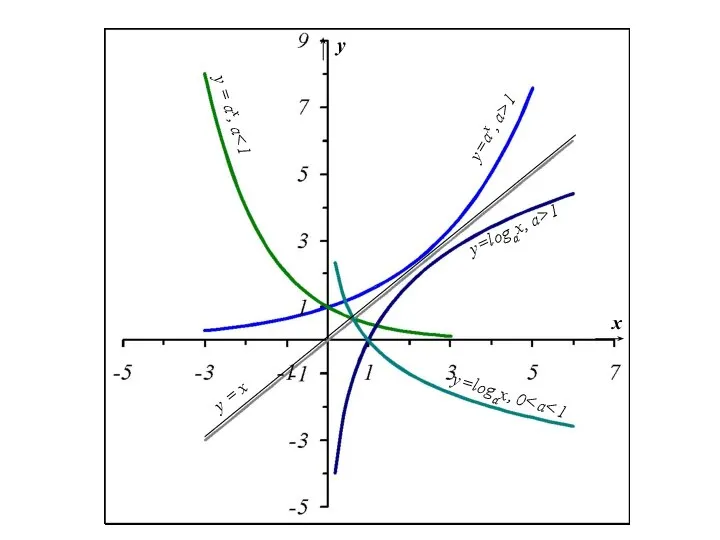
- 36. 2). Показательная функция y = ax, a>0, a≠1
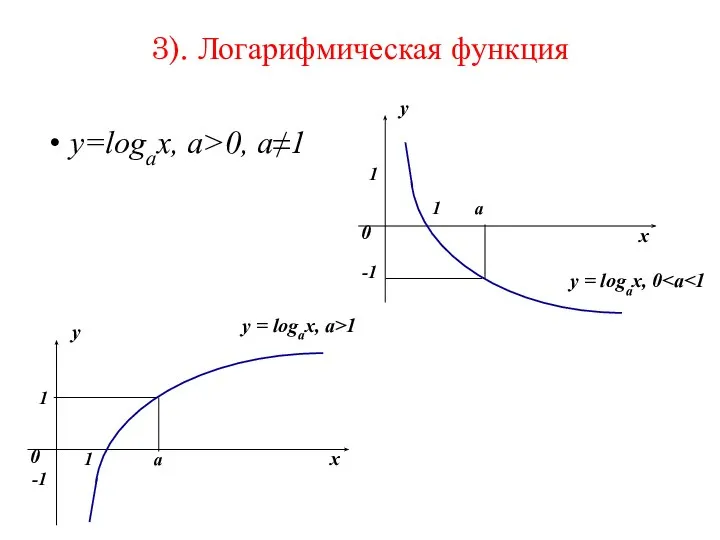
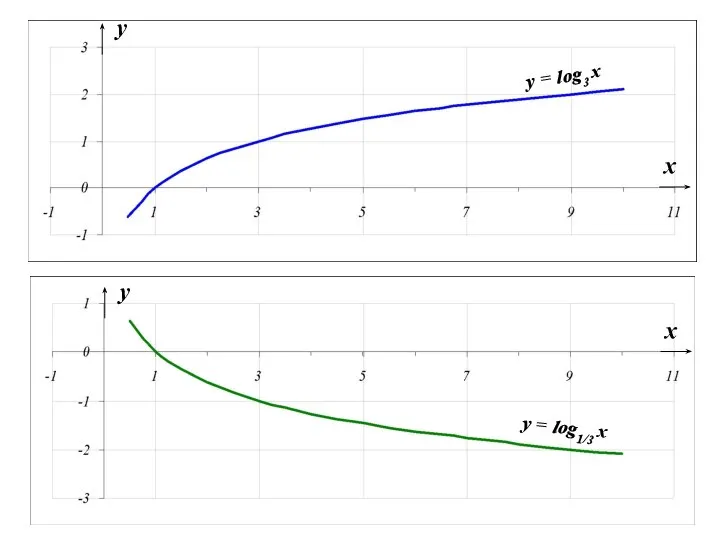
- 39. 3). Логарифмическая функция y=logax, a>0, a≠1
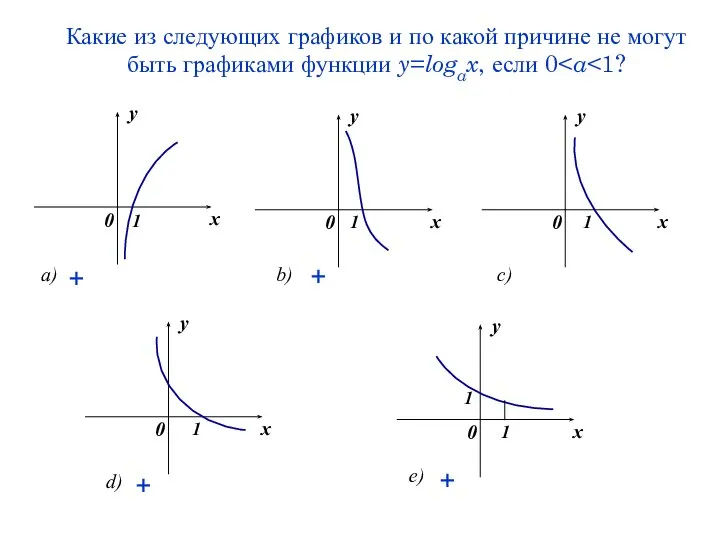
- 41. Какие из следующих графиков и по какой причине не могут быть графиками функции y=logax, если 0
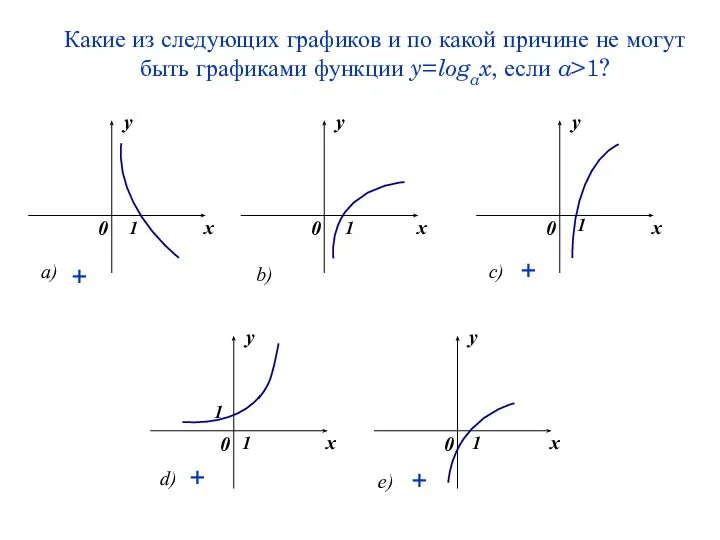
- 42. Какие из следующих графиков и по какой причине не могут быть графиками функции y=logax, если a>1?
- 44. 4). Тригонометрические функции y = sin x y = cos x y = tan x y
- 45. y = sin x График функции – синусоида sin (-x) = - sin (x) sin (x+2πk)
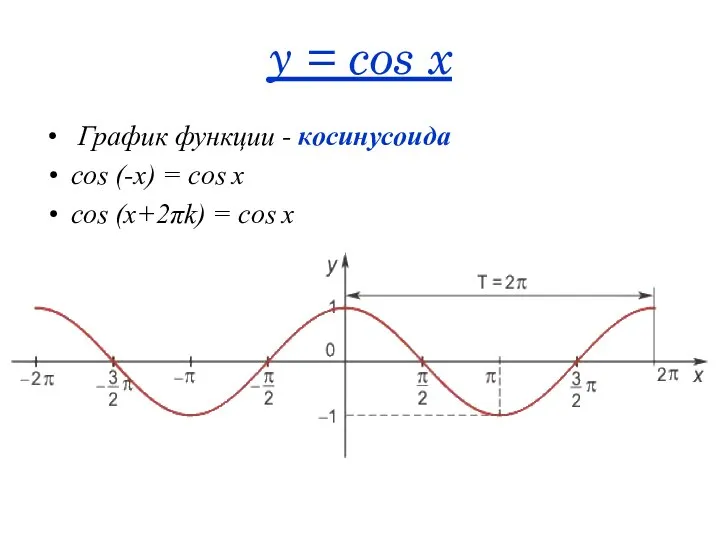
- 46. y = cos x График функции - косинусоида cos (-x) = cos x cos (x+2πk) =
- 47. y = tan x График функции – тангенсоида tan (-x) = - tan x tan (x+πk)
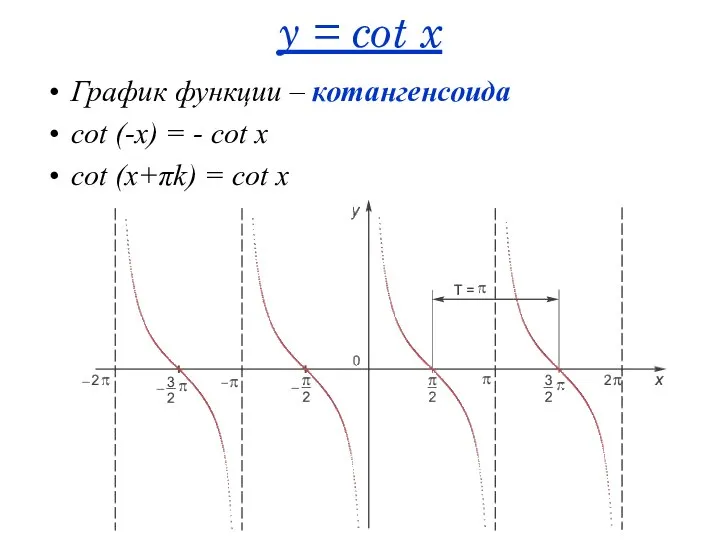
- 48. y = cot x График функции – котангенсоида cot (-x) = - cot x cot (x+πk)
- 49. 5). Обратные тригонометрические функции y = arcsin x y = arccos x y = arctan x
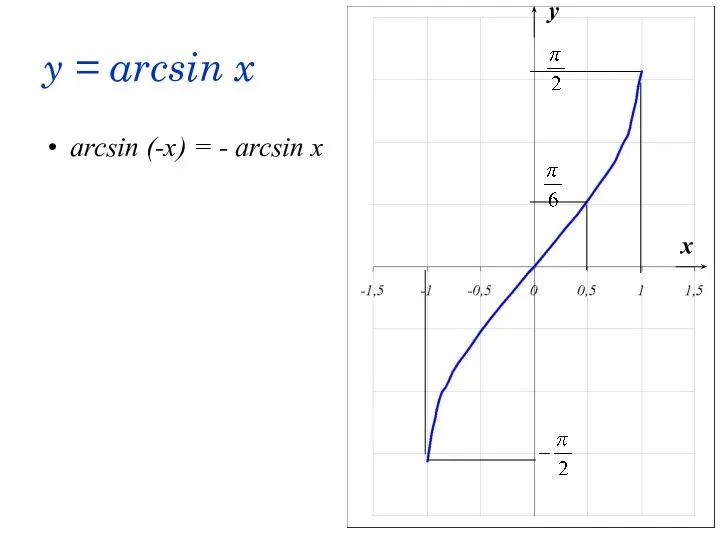
- 50. y = arcsin x arcsin (-x) = - arcsin x
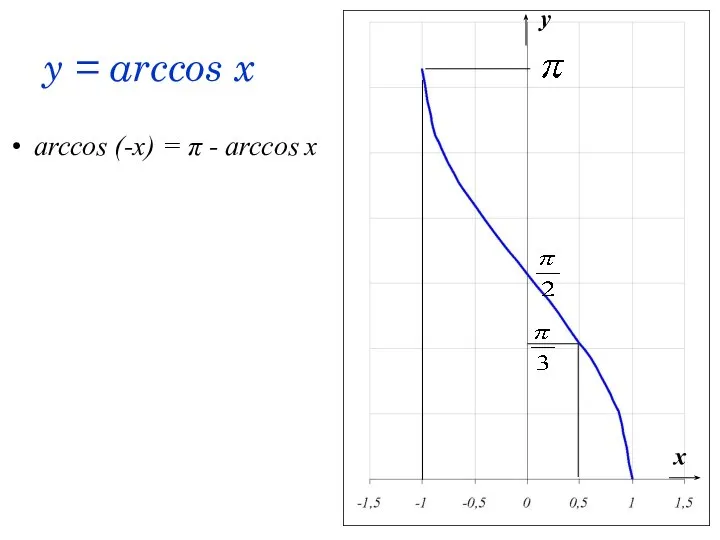
- 51. y = arccos x arccos (-x) = π - arccos x
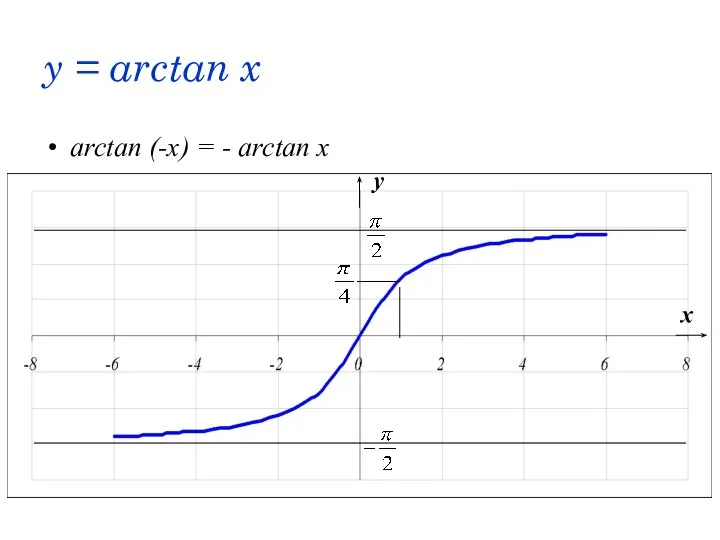
- 52. y = arctan x arctan (-x) = - arctan x
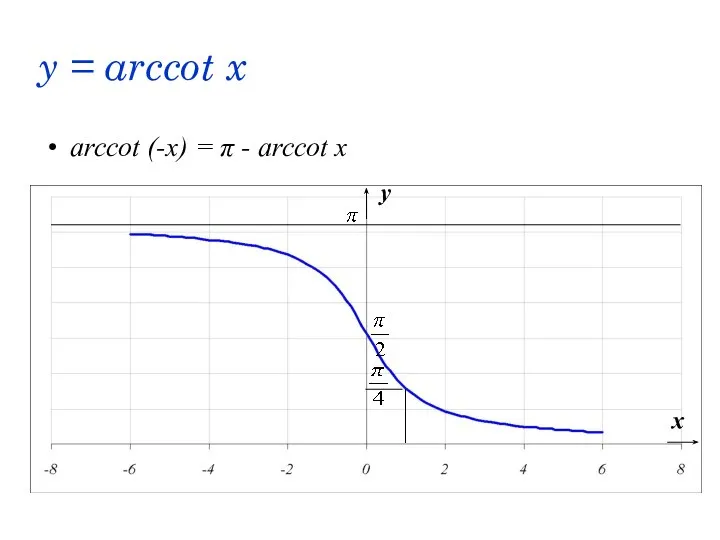
- 53. y = arccot x arccot (-x) = π - arccot x
- 54. Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических
- 55. Примеры неэлементарных функций: (Количество операций, которое нужно произвести для получения у, не является ограниченным)
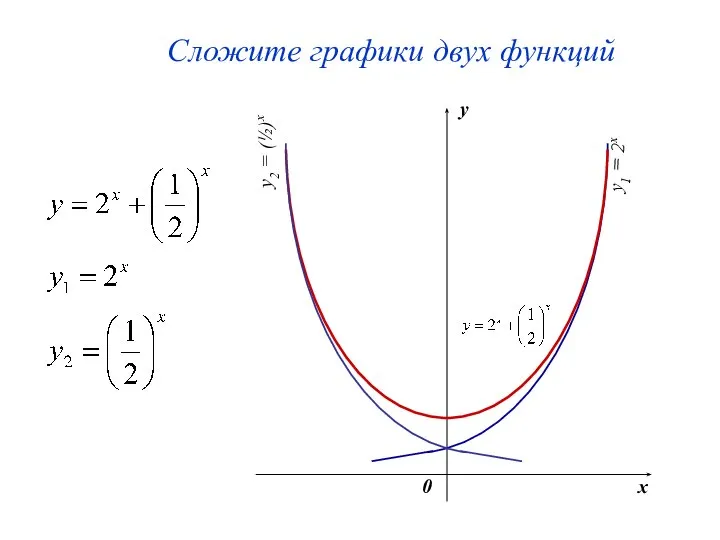
- 56. 5. Сложение графиков функций Чтобы сложить графики функций нужно сложить их ординаты. y = y1+y2
- 57. Сложите графики двух функций
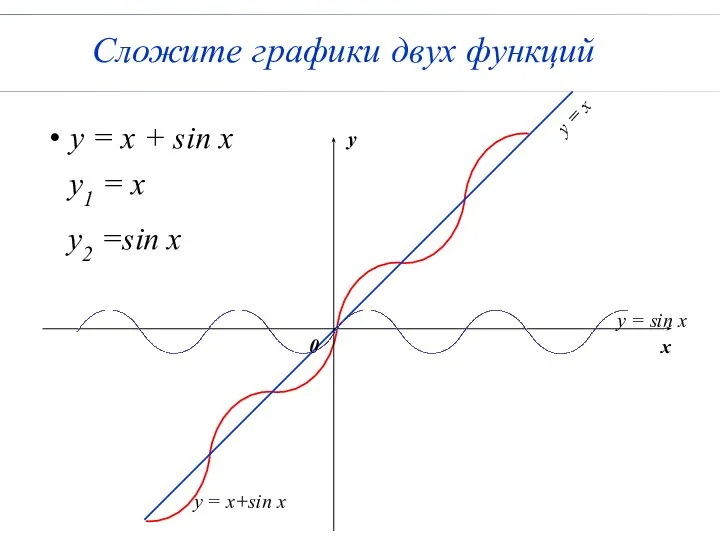
- 58. Сложите графики двух функций y = x + sin x y1 = x y2 =sin x
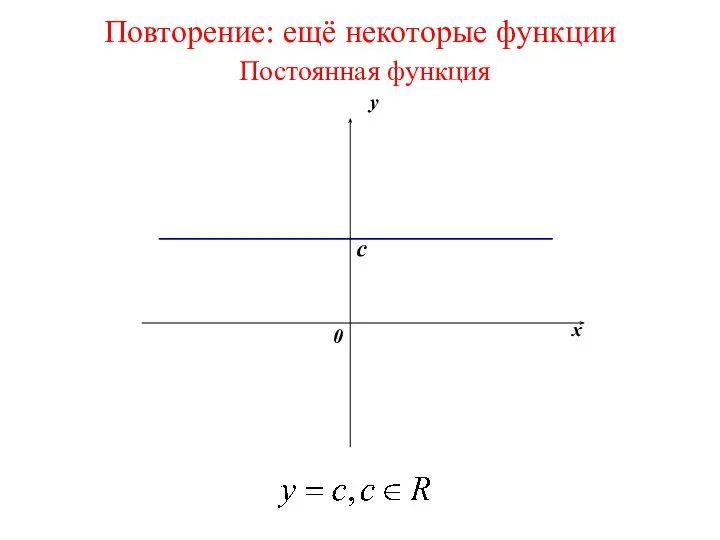
- 59. Повторение: ещё некоторые функции Постоянная функция y
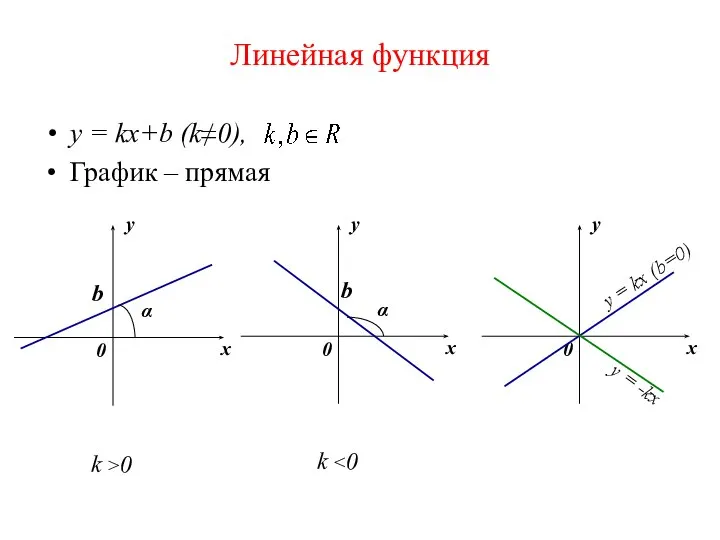
- 60. Линейная функция y = kx+b (k≠0), График – прямая y = -kx y = kx (b=0)
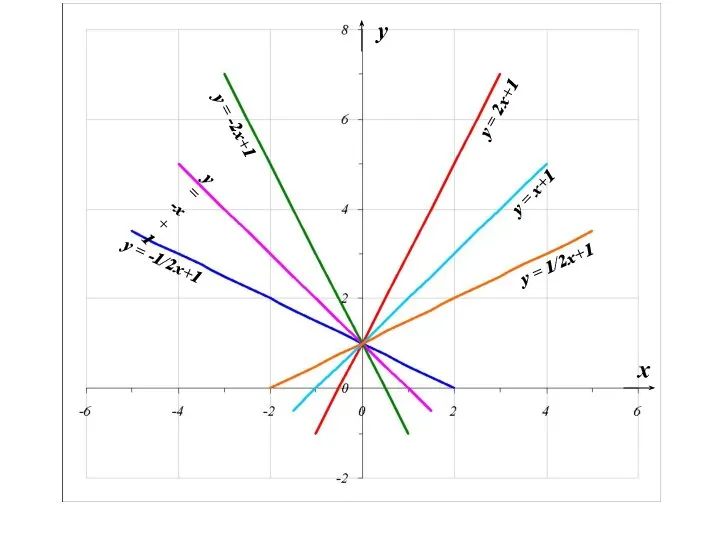
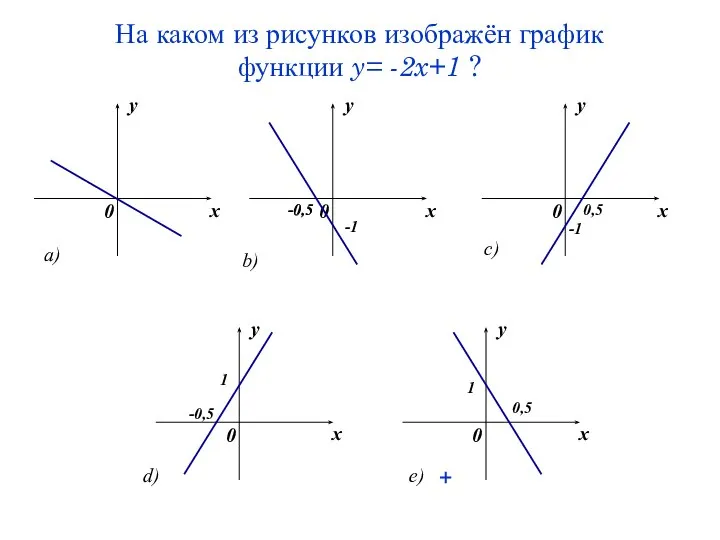
- 62. На каком из рисунков изображён график функции y= -2x+1 ? +
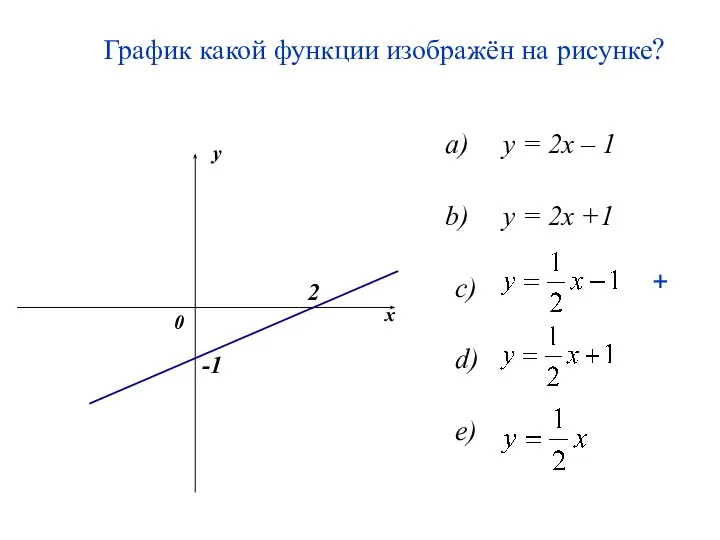
- 63. График какой функции изображён на рисунке? y = 2x – 1 y = 2x +1 c)
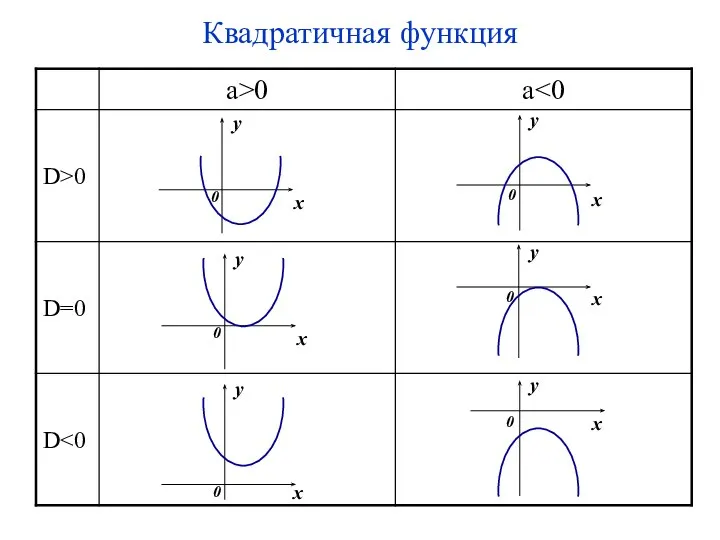
- 64. Квадратичная функция y = ax2+bx+c, , a ≠ 0 График – парабола
- 65. Квадратичная функция y
- 67. Скачать презентацию












 Факториальные кольца
Факториальные кольца Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями Вычисление площадей плоских фигур с помощью определенного интеграла (3)
Вычисление площадей плоских фигур с помощью определенного интеграла (3) Тригонометрия. Комплексные числа
Тригонометрия. Комплексные числа Сфера и шар. Решение задач
Сфера и шар. Решение задач Презентацию выполнил: ученик 6 класса МБОУ «СОШ № 24» п. Снежногорск, Красноярского края Корыткин Илья Руководитель: учитель мате
Презентацию выполнил: ученик 6 класса МБОУ «СОШ № 24» п. Снежногорск, Красноярского края Корыткин Илья Руководитель: учитель мате Презентация на тему Взаимно обратные числа - деление
Презентация на тему Взаимно обратные числа - деление  Числовые и буквенные выражения. (5 класс)
Числовые и буквенные выражения. (5 класс) Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Презентация по математике "Прямая пропорциональность и ее график" - скачать
Презентация по математике "Прямая пропорциональность и ее график" - скачать  Призма
Призма Игра по математике для 6 класса «Счастливый случай»
Игра по математике для 6 класса «Счастливый случай» Обыкновенные дроби. Урок-соревнование «Крестики-нолики»
Обыкновенные дроби. Урок-соревнование «Крестики-нолики» Задание 2. Задача минимизировать время сбора утром на работу и в школу семьи из трех человек: отец, сын (10 лет), дочь (6 лет)
Задание 2. Задача минимизировать время сбора утром на работу и в школу семьи из трех человек: отец, сын (10 лет), дочь (6 лет) Многочлены от одной переменной
Многочлены от одной переменной Степени и корни
Степени и корни Числа вокруг нас
Числа вокруг нас Системы линейных алгебраических уравнений (СЛАУ)
Системы линейных алгебраических уравнений (СЛАУ) Площади и объёмы фигур
Площади и объёмы фигур Среднее арифметическое. Деление десятичной дроби на натуральное число
Среднее арифметическое. Деление десятичной дроби на натуральное число Численное интегрирование
Численное интегрирование Definition. Statistics
Definition. Statistics Координатная плоскость
Координатная плоскость Вычисления с многозначными числами
Вычисления с многозначными числами Степень с отрицательным целым показателем
Степень с отрицательным целым показателем Перевод процентов в десятичную дробь, а дробь в проценты
Перевод процентов в десятичную дробь, а дробь в проценты РЕШЕНИЕ НЕРАВЕНСТВ (НАЙДИ ОШИБКУ) 8 класс
РЕШЕНИЕ НЕРАВЕНСТВ (НАЙДИ ОШИБКУ) 8 класс  Регрессионный анализ. Эмпирические модели. Понятия регрессии. Уравнение линейной регрессии. (Лекция 9)
Регрессионный анализ. Эмпирические модели. Понятия регрессии. Уравнение линейной регрессии. (Лекция 9)