Содержание
- 2. Специальные классы булевых функций Американский математик Эмиль Пост ввел в рассмотрение следующие замкнутые классы булевых функций:
- 3. Класс функций, сохраняющих константу 0 Определение. Говорят, что функция сохраняет константу 0, если f(0,0,…,0)=0 Примеры: f(x,y)=x⊕y
- 4. Определение. Говорят, что функция сохраняет константу 1, если f(1,1,…,1)=1 Примеры: f(x,y)=x~y f(x,y)=x·y Класс функций, сохраняющих константу
- 5. Двойственность Пусть f(x1, x2, …, xn ) – булева функция. Двойственной к ней называется функция f*,
- 6. Класс самодвойственных булевых функций Определение. Булева функция f(x1,…,xn) самодвойственна (принадлежит классу S), если она равна двойственной
- 7. Пример самодвойственной функции f(x,y,z)=xy+yz+xz
- 8. Алгоритм распознавания самодвойственной функции, заданной таблицей истинности для проверки самодвойственности булевой функции можно не получать двойственную
- 9. Являются ли функции f(x,y,z), g(x,y,z), h(x,y,z) самодвойственными? Задача:
- 10. Сравнимые наборы Два набора и называются сравнимыми ( ), если Запись означает, что набор α предшествует
- 11. Класс монотонных функций Определение. Булева функция f(x1, …, xn) называется монотонной (принадлежит классу M), если для
- 12. Является ли функция монотонной? Из элементарных булевых функций монотонными являются, например, конъюнкция и дизъюнкция. Не являются
- 13. Класс линейных функций Определение. Булева функция называется линейной (принадлежит классу L), если ее полином Жегалкина линеен.
- 15. Функциональная полнота системы булевых функций
- 16. Определение ФПС Определение. Множество функций N называется функционально полной системой (ФПС), если любая булева функция представима
- 17. Примеры ФПС Пример 1. Множество N1={&,+,–} является функционально полной системой, так как любую булеву функцию, кроме
- 18. Теорема о двух функционально полных системах Теорема. Если даны два множества N1 и N2 булевых функций
- 19. Пример. N1={&,+,–}, N2={&, –}. Как показано ранее, N1 – ФПС. Конъюнкция и инверсия содержатся в N2,
- 20. Задание: Докажите, что система функций {¬, v} является полной. Пусть f1(x1) = x1 f2(x1, x2) =
- 21. Существует функционально полная система, состоящая из одной булевой функции. Штрих Шеффера (И-НЕ) – x1 | x2
- 22. Доказательство x1 | x2 = x1 v x2 или x1 | x2 = x1 & x2
- 23. Стрелка Пирса (ИЛИ-НЕ) – x1 ↓ x2 Функция стрелка Пирса является полной. x1 ↓ x2 =
- 24. Теорема Поста Теорема (о полноте). Для того, чтобы система булевых функций Д была полной, необходимо и
- 25. Таблицы Поста В тех задачах, где требуется выяснить, является ли данная система {f1 f2, …, fn}
- 26. Пример. Выяснить, являются ли следующие системы булевых функций полными. Являются ли следующие системы булевых функций базисами.
- 29. Скачать презентацию


























 Игра. Сосчитай зайчиков (начальная школа)
Игра. Сосчитай зайчиков (начальная школа) Дроби в музыке
Дроби в музыке Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Наглядное пособие по математике «Объем прямоугольного параллелепипеда» Автор проекта: Мигачева Ольга, ученица 8А класса Лаишевс
Наглядное пособие по математике «Объем прямоугольного параллелепипеда» Автор проекта: Мигачева Ольга, ученица 8А класса Лаишевс Приведение дробей к общему знаменателю. (6 класс)
Приведение дробей к общему знаменателю. (6 класс)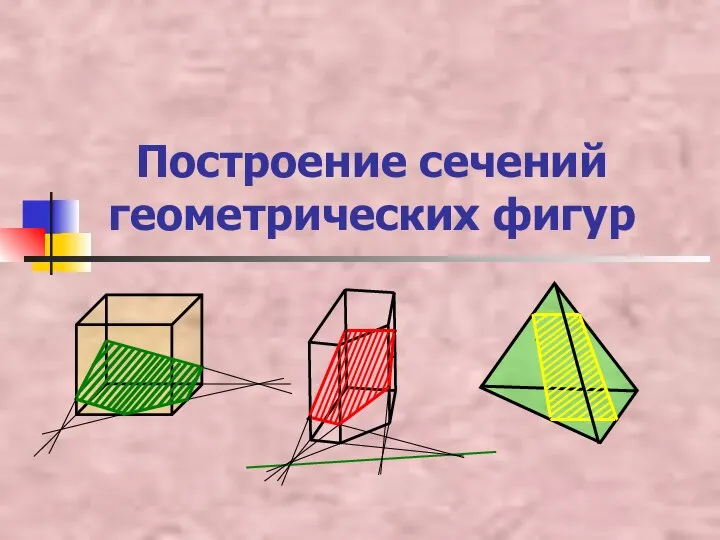 Построение сечений геометрических фигур
Построение сечений геометрических фигур Обыкновенные дифференциальные уравнения Лекция 4
Обыкновенные дифференциальные уравнения Лекция 4  Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Повторение по математике, 6 класс
Повторение по математике, 6 класс Случайные величины и их числовые характеристики
Случайные величины и их числовые характеристики Решение задач. Подготовка к контрольной работе
Решение задач. Подготовка к контрольной работе Сложение и вычитание чисел от 1 до 10 (часть 2)
Сложение и вычитание чисел от 1 до 10 (часть 2) Математическая игра-раскраска
Математическая игра-раскраска Применение ППП SPSS. Statistica и SAS для статистических анализов медико-биологических данных
Применение ППП SPSS. Statistica и SAS для статистических анализов медико-биологических данных Деление десятичных дробей на натуральные числа. Тест. (5 класс)
Деление десятичных дробей на натуральные числа. Тест. (5 класс) Пьер Ферма
Пьер Ферма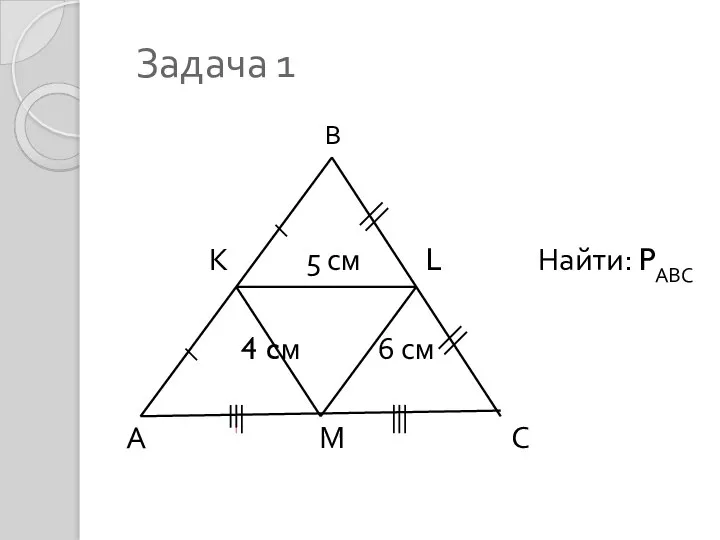 Средняя линия треугольника
Средняя линия треугольника Свойства числовых неравенств
Свойства числовых неравенств Нахождение разности двух чисел
Нахождение разности двух чисел Тригонометрия
Тригонометрия Квадратные корни. 8 класс
Квадратные корни. 8 класс Измерение углов
Измерение углов Презентация для класса Оценка произведения
Презентация для класса Оценка произведения  Задачи на нахождение остатка . Часть 2
Задачи на нахождение остатка . Часть 2 Векторы. Понятие вектора
Векторы. Понятие вектора Прямоугольный параллелепипед. 5 класс
Прямоугольный параллелепипед. 5 класс Многоугольники
Многоугольники Arctg, arcctg. Решение уравнений tgt=a, ctgt=a
Arctg, arcctg. Решение уравнений tgt=a, ctgt=a