Содержание
- 2. При изучении многих явлений приходится сталкиваться с функциями двух и более переменных. Определение функции двух переменных
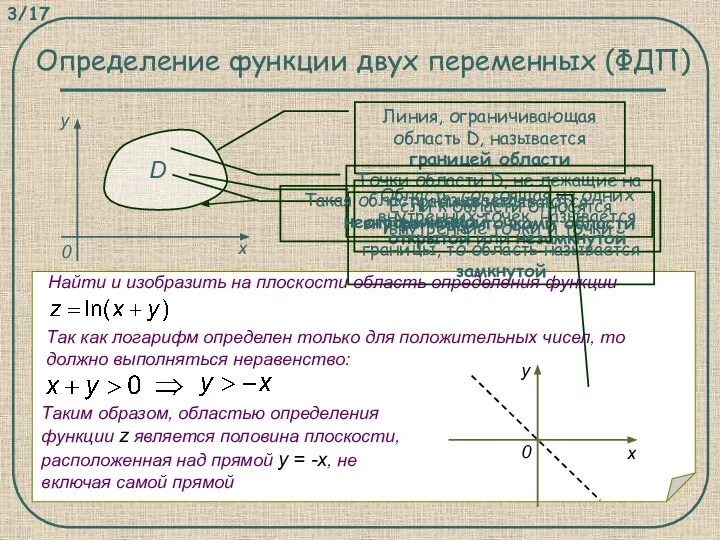
- 3. Определение функции двух переменных (ФДП) D Линия, ограничивающая область D, называется границей области Точки области D,
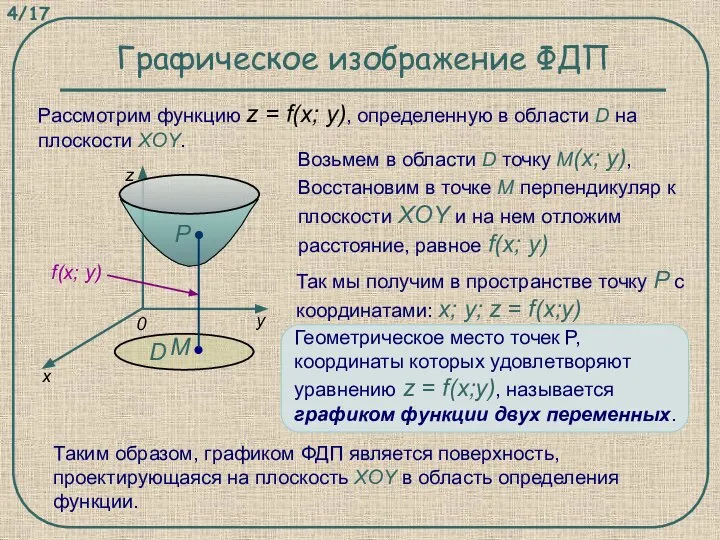
- 4. Рассмотрим функцию z = f(x; y), определенную в области D на плоскости XOY. Графическое изображение ФДП
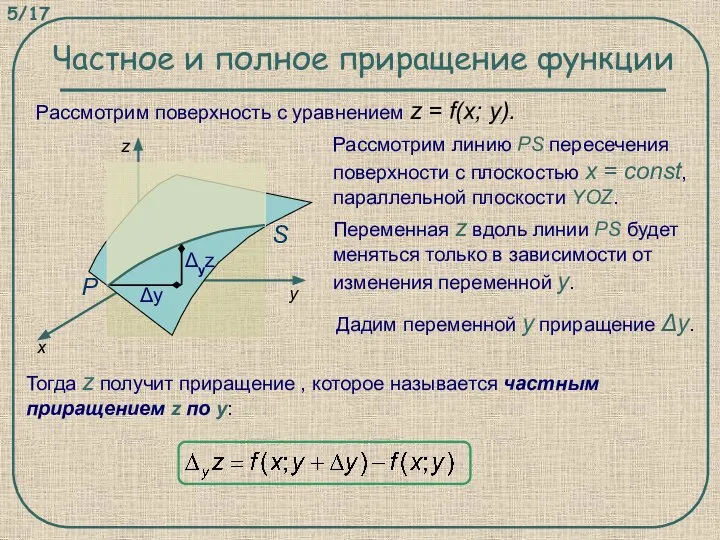
- 5. Рассмотрим поверхность с уравнением z = f(x; y). Частное и полное приращение функции Тогда z получит
- 6. Частное и полное приращение функции Дадим переменной x приращение Δx , тогда z получит приращение ,
- 7. Частные производные ФДП Частной производной по х от функции z = f(x;y) называется предел отношения частного
- 8. Частные производные ФДП Заметив, что Δxz вычисляется при неизменном y, а Δyz при неизменном x, можно
- 9. Полный дифференциал ФДП Если функция z = f(x;y) имеет непрерывные частные производные в некоторой точке, то
- 10. Полный дифференциал ФДП В этом выражении γ1 и γ2 - бесконечно малые функции когда Δx и
- 11. Полный дифференциал ФДП Вычислить приближенно: Введем функцию: Необходимо вычислить значение этой функции в точке (3,01; 4,02)
- 12. Производная сложной функции Предположим, что в уравнении: u и v являются функциями независимых переменных x и
- 13. Производная сложной функции Вычислить частные производные функции z по переменным x и y. Подставим найденные производные
- 14. Производная сложной функции Если задана функция где u и v зависят только от одной переменной x
- 16. Скачать презентацию










 Задача 34
Задача 34 Математические игры
Математические игры Презентация по математике "Сложение и вычитание двузначных чисел" - скачать бесплатно
Презентация по математике "Сложение и вычитание двузначных чисел" - скачать бесплатно Действия с обыкновенными дробями. Создание открытого акционерного общества
Действия с обыкновенными дробями. Создание открытого акционерного общества Метод резолюций в исчислении предикатов
Метод резолюций в исчислении предикатов Дидактическая игра. Знатоки истоков математики. 6 класс
Дидактическая игра. Знатоки истоков математики. 6 класс Математика-это наука или практика? Логарифмические спирали. Применение в жизни.
Математика-это наука или практика? Логарифмические спирали. Применение в жизни. Презентация по математике "Инструменты, приборы и приспособления для вычислений" - скачать
Презентация по математике "Инструменты, приборы и приспособления для вычислений" - скачать  Статистика. «Статистика знает всё» (Ильф и Петров). Выборочные исследования
Статистика. «Статистика знает всё» (Ильф и Петров). Выборочные исследования Презентация на тему Деление
Презентация на тему Деление  Аттестационная работа. Исследовательская и проектная деятельность учащихся на уроках математики
Аттестационная работа. Исследовательская и проектная деятельность учащихся на уроках математики Распределительное свойство умножения
Распределительное свойство умножения Неравенства с одной переменной. Метод интервалов
Неравенства с одной переменной. Метод интервалов Витамины и математика
Витамины и математика Титло
Титло Векторный анализ. Лекция 4
Векторный анализ. Лекция 4 Solid geometry
Solid geometry Модуль действительного числа и его свойства
Модуль действительного числа и его свойства Представление результатов измерений
Представление результатов измерений Математическое кафе Функция
Математическое кафе Функция Признаки делимости на 3 и 9
Признаки делимости на 3 и 9 Логические задачи
Логические задачи Решение уравнений
Решение уравнений Устные приемы сложения вида 26+7, 64+9
Устные приемы сложения вида 26+7, 64+9 Основные понятия. Классическое определение вероятности
Основные понятия. Классическое определение вероятности МИР СИММЕТРИИ И СИММЕТРИЯ МИРА
МИР СИММЕТРИИ И СИММЕТРИЯ МИРА  Координатная плоскость и знаки зодиака
Координатная плоскость и знаки зодиака Прогрессии в окружающей нас жизни
Прогрессии в окружающей нас жизни