Содержание
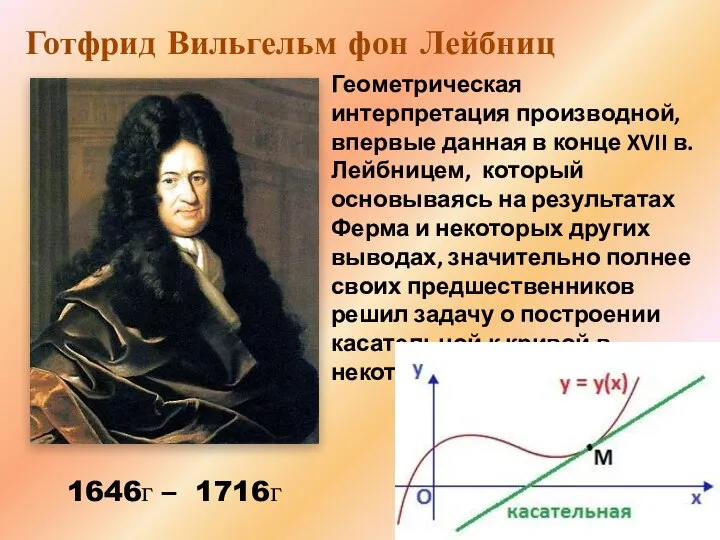
- 2. Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, который основываясь на результатах Ферма и
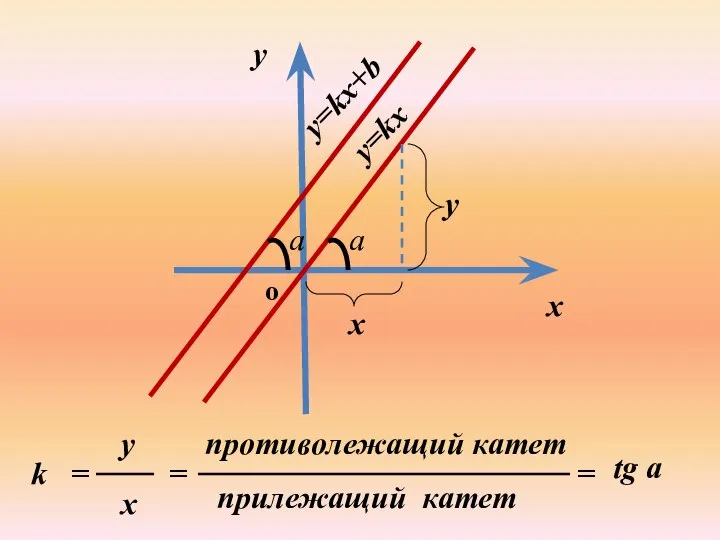
- 3. y=kx k = x y = противолежащий катет прилежащий катет = tg a a y x
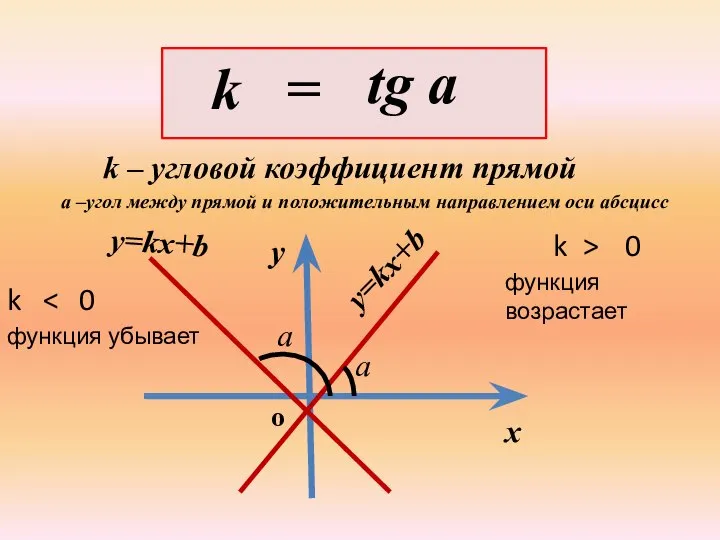
- 4. k = tg a k – угловой коэффициент прямой а –угол между прямой и положительным направлением
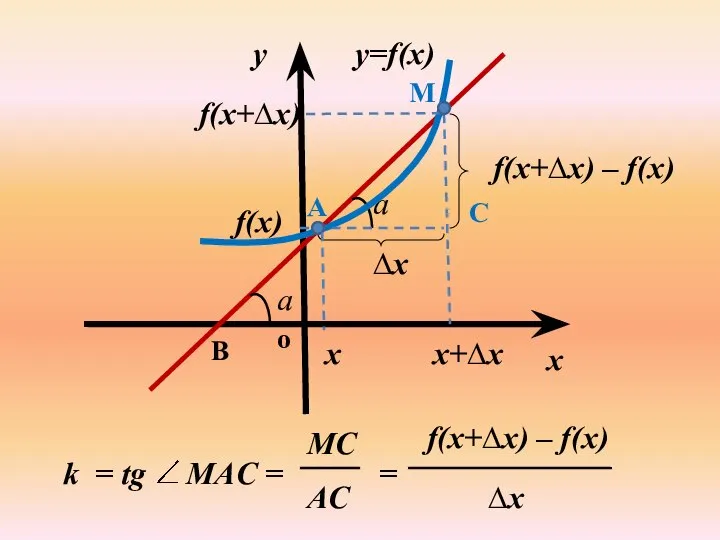
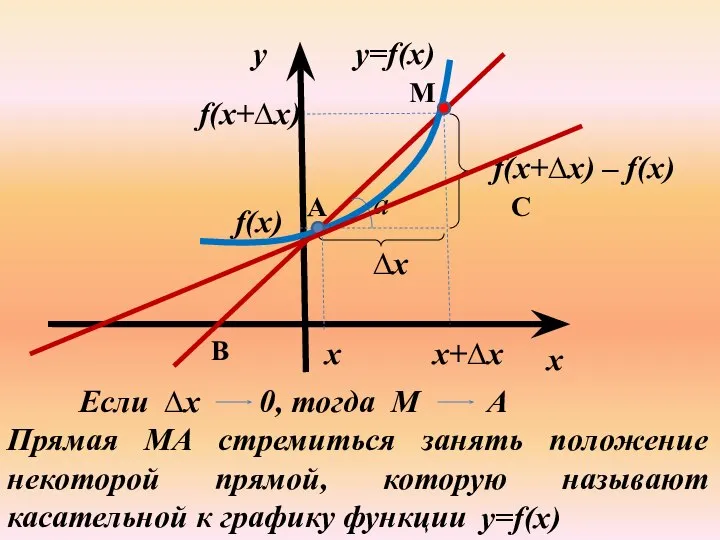
- 5. y=f(x) a x y x M B C A x+∆х f(x) f(x+∆х) f(x+∆х) – f(x) ∆х
- 6. y=f(x) a x y x M B C A x+∆х f(x) f(x+∆х) f(x+∆х) – f(x) ∆х
- 7. f(x+∆х) – f(x) ∆х = lim k = f ' (x) k = tg a f
- 8. tga tga = 0 k > 0 f'(x ) > 0 f'(x ) f'(x ) =
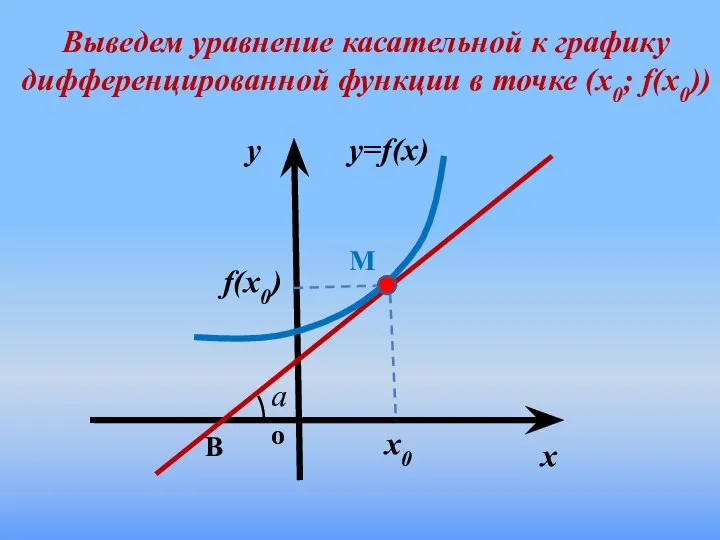
- 9. Выведем уравнение касательной к графику дифференцированной функции в точке (х0; f(x0))
- 10. y=kx +b k = tg a f ' (x) = y=f' (x0 )x+ b Т.к. касательная
- 11. Алгоритм нахождения уравнения касательной к графику функции y=f(x) в точке с абсциссой х0 f(x0) – находим
- 12. Решаем задачи № 857-861 (только нечетные)
- 15. Скачать презентацию






 Интегрирование. Определенный интеграл
Интегрирование. Определенный интеграл Векторное исчисление
Векторное исчисление Презентация по математике "Математическое образование в петровскую эпоху" - скачать
Презентация по математике "Математическое образование в петровскую эпоху" - скачать  Числовые выражения. Выражения с переменной. Уравнения. Математическая модель
Числовые выражения. Выражения с переменной. Уравнения. Математическая модель Умножение. Множители. Произведение
Умножение. Множители. Произведение Действия с одночленами
Действия с одночленами Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Сравнение десятичных дробей.
Сравнение десятичных дробей. Поле чудес. Геометрия 9 класс
Поле чудес. Геометрия 9 класс Математическое описание линейных САУ. Дифференциальные уравнения, передаточная функция. Временные и частотные характеристики
Математическое описание линейных САУ. Дифференциальные уравнения, передаточная функция. Временные и частотные характеристики Прямоугольные треугольники. Задания для устного счета
Прямоугольные треугольники. Задания для устного счета Площадь треугольника и медиана
Площадь треугольника и медиана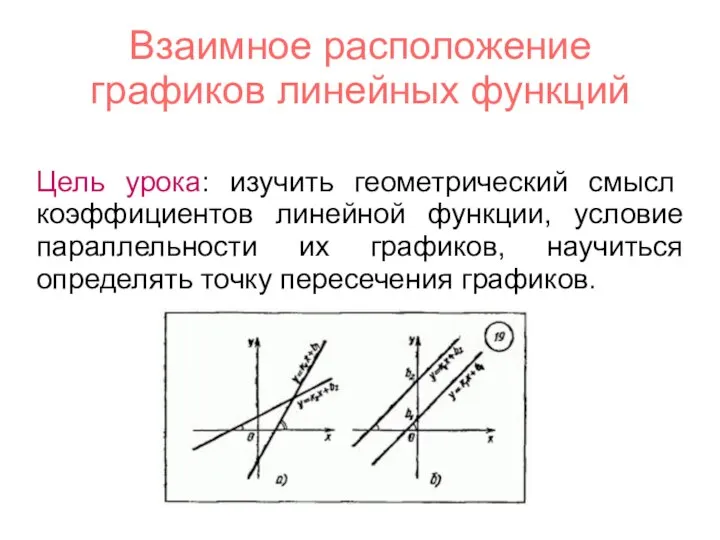 Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Решение задач с помощью рациональных уравнений. 8 класс
Решение задач с помощью рациональных уравнений. 8 класс Умножение рациональных чисел
Умножение рациональных чисел Иррациональные числа
Иррациональные числа Бином Ньютона и треугольник Паскаля
Бином Ньютона и треугольник Паскаля Появление дробей. 5 класс
Появление дробей. 5 класс Умножение дробей на натуральное число
Умножение дробей на натуральное число Некоторые свойства касательной к окружности
Некоторые свойства касательной к окружности Презентация по математике "Сложение и вычитание чисел в пределах 20" - скачать бесплатно
Презентация по математике "Сложение и вычитание чисел в пределах 20" - скачать бесплатно Умножение десятичных дробей
Умножение десятичных дробей Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Подготовка к ЕГЭ по математике. Задания, 11 класс
Подготовка к ЕГЭ по математике. Задания, 11 класс Второй признак равенства треугольников
Второй признак равенства треугольников Extracurricular study in mathematics, 7th grade
Extracurricular study in mathematics, 7th grade Степень числа. 5 класс
Степень числа. 5 класс Диаграммы. Виды диаграмм
Диаграммы. Виды диаграмм