Содержание
- 2. Эйлеровы графы Мы уже упоминали работу Эйлера, датированную 1736 годом, которая положила начало теории графов. В
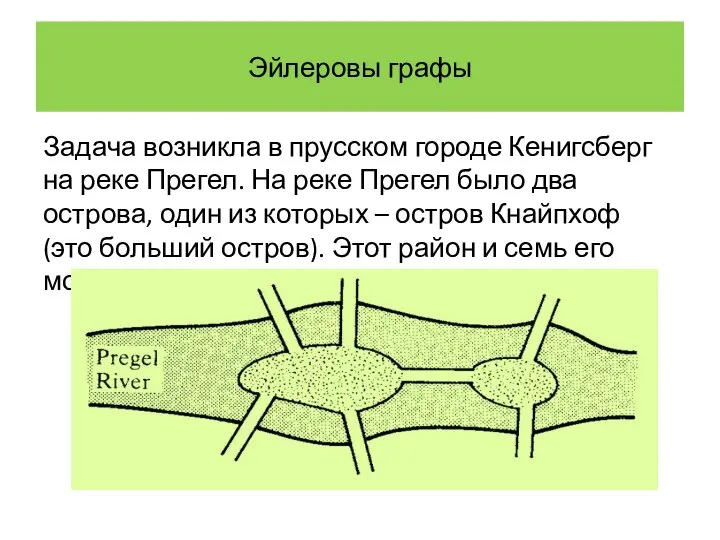
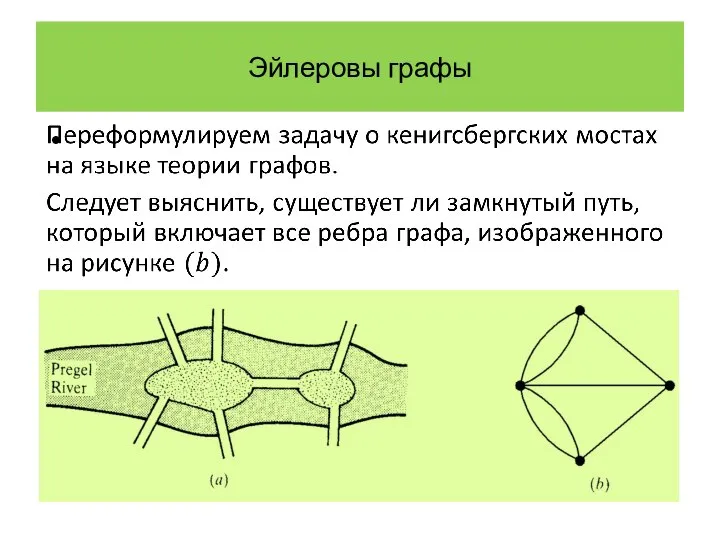
- 3. Эйлеровы графы Задача возникла в прусском городе Кенигсберг на реке Прегел. На реке Прегел было два
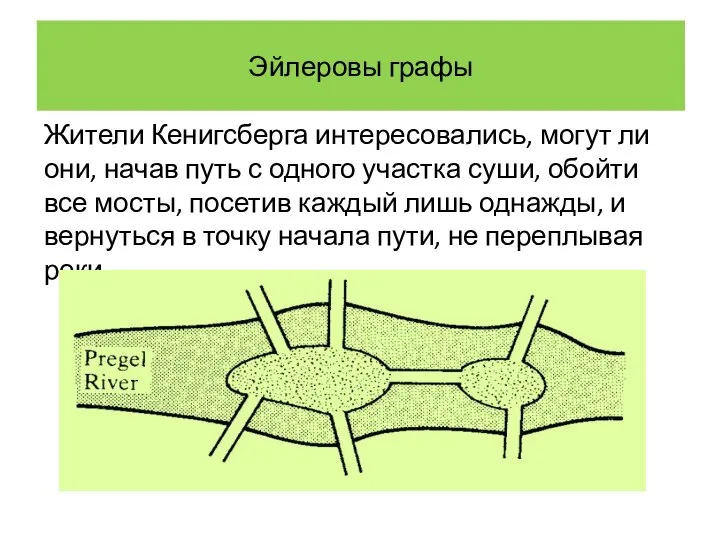
- 4. Эйлеровы графы Жители Кенигсберга интересовались, могут ли они, начав путь с одного участка суши, обойти все
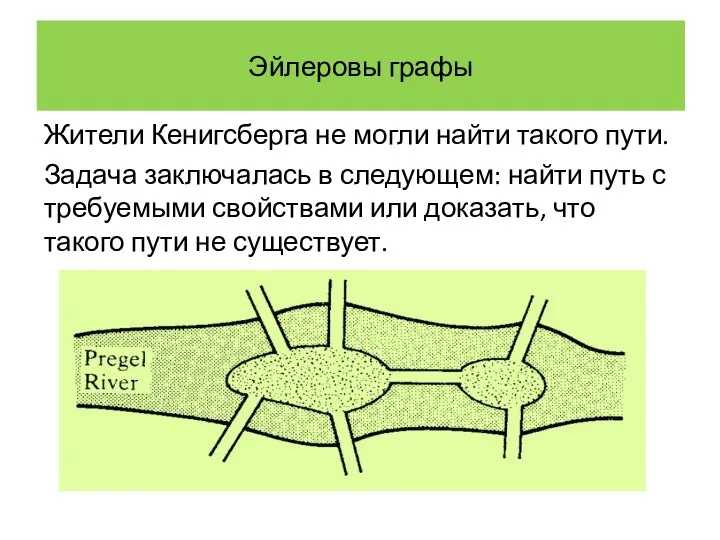
- 5. Эйлеровы графы Жители Кенигсберга не могли найти такого пути. Задача заключалась в следующем: найти путь с
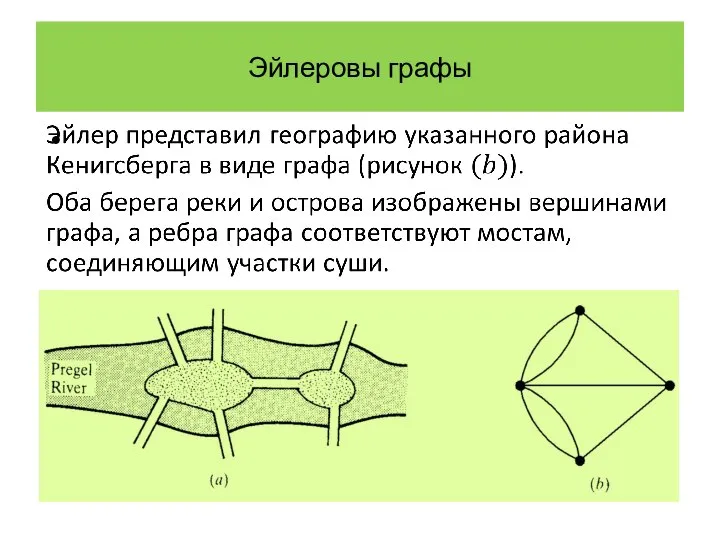
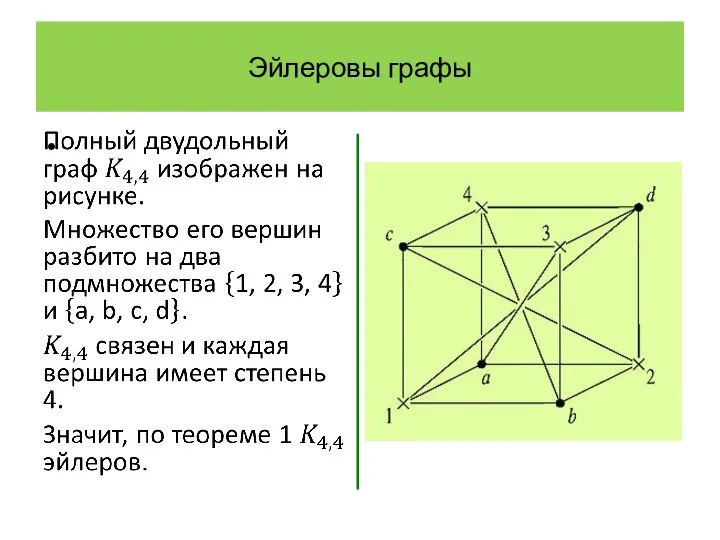
- 6. Эйлеровы графы
- 7. Эйлеровы графы
- 8. Эйлеровы графы
- 9. Эйлеровы графы
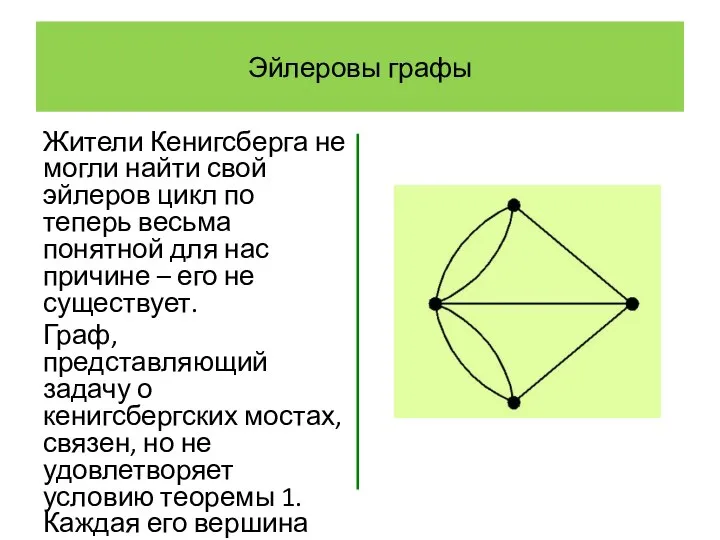
- 13. Эйлеровы графы Жители Кенигсберга не могли найти свой эйлеров цикл по теперь весьма понятной для нас
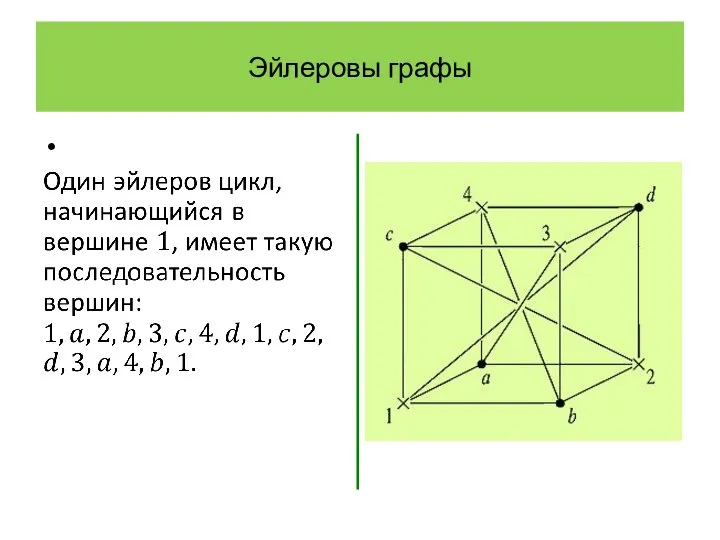
- 14. Эйлеровы графы
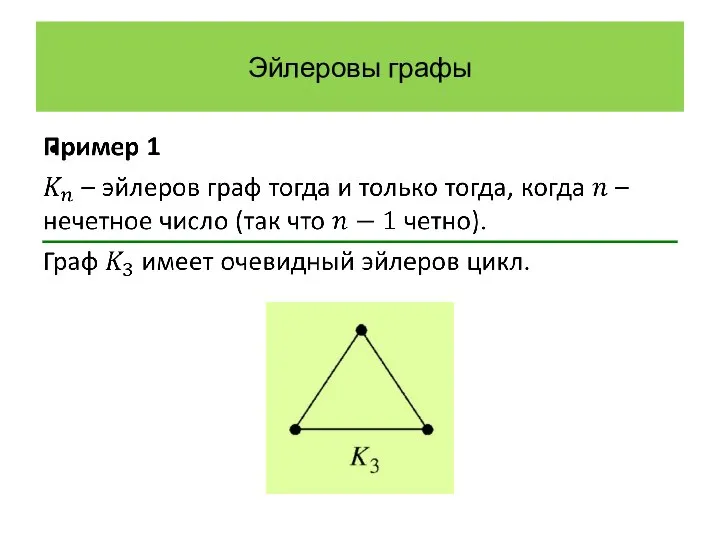
- 15. Эйлеровы графы
- 16. Эйлеровы графы
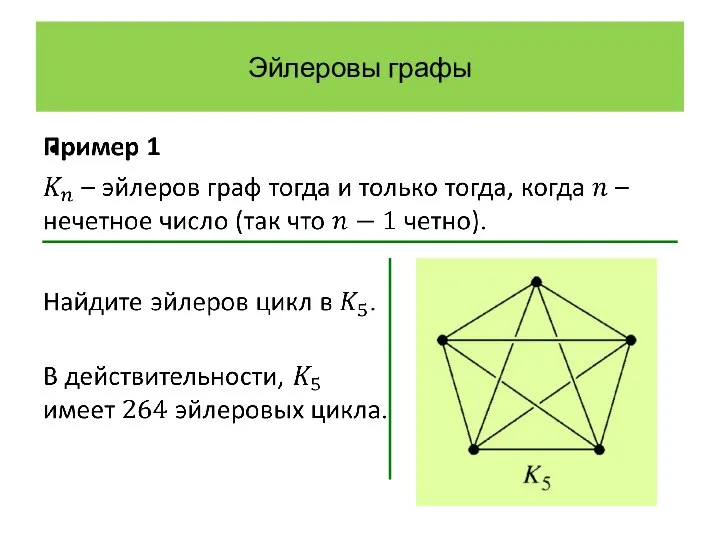
- 17. Эйлеровы графы
- 18. Эйлеровы графы
- 19. Гамильтоновы графы Эйлеров цикл проходит через каждое ребро графа (один раз) и возвращается в начальную точку
- 20. Гамильтоновы графы Определение 2 Гамильтонов цикл в графе – это цикл, который проходит через каждую вершину
- 21. Гамильтоновы графы Сэр Уильям Роуэн Гамильтон (1805 – 1865) был выдающимся ирландским математиком. Закончив университет, в
- 22. Гамильтоновы графы В 1843 он открыл кватернионы – одну из разновидностей обобщения комплексных чисел – и
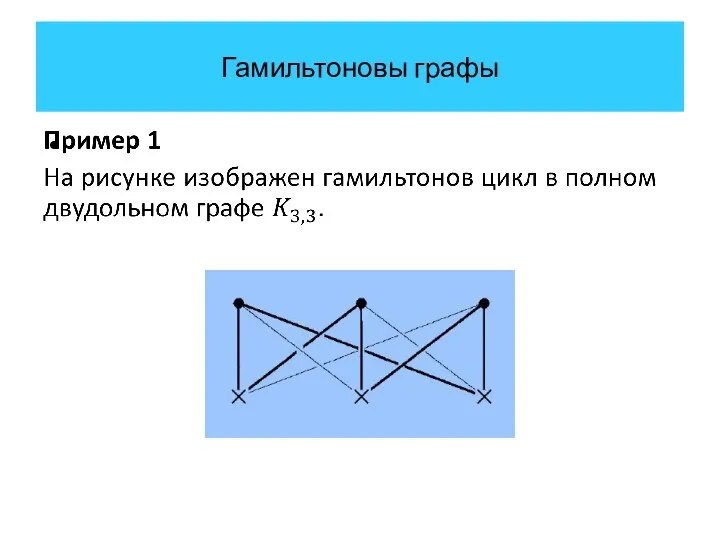
- 23. Гамильтоновы графы Итак, в 1857 году Уильям Роуэн Гамильтон придумал игру. Существует несколько версий того, как
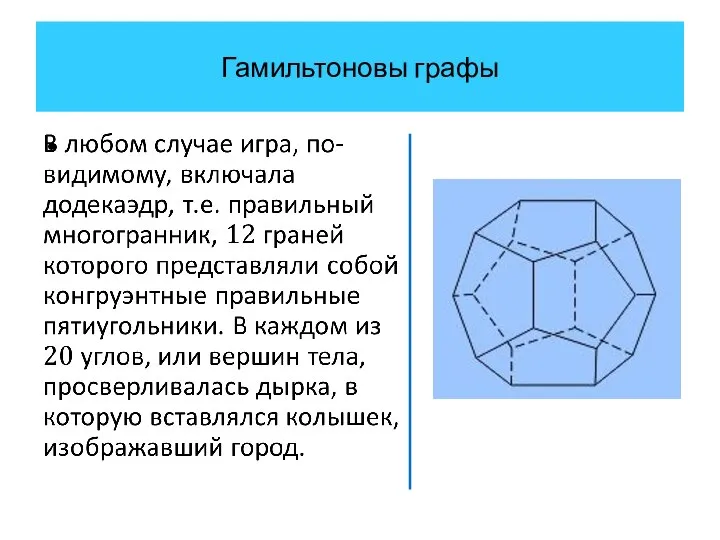
- 24. Гамильтоновы графы
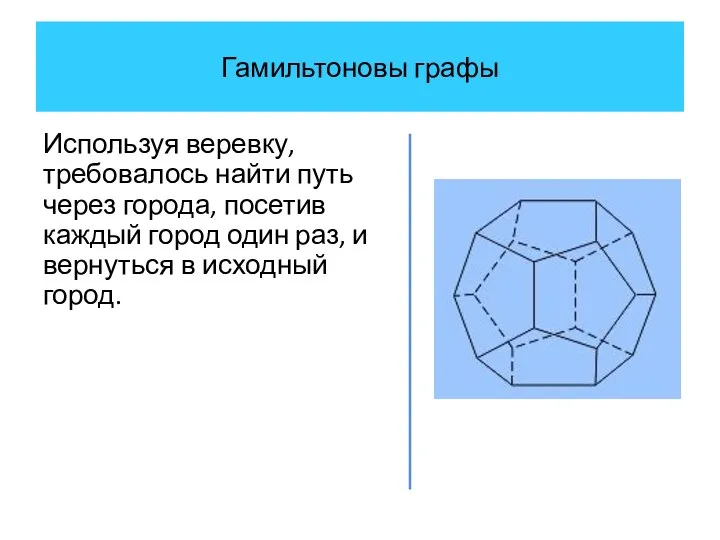
- 25. Гамильтоновы графы Используя веревку, требовалось найти путь через города, посетив каждый город один раз, и вернуться
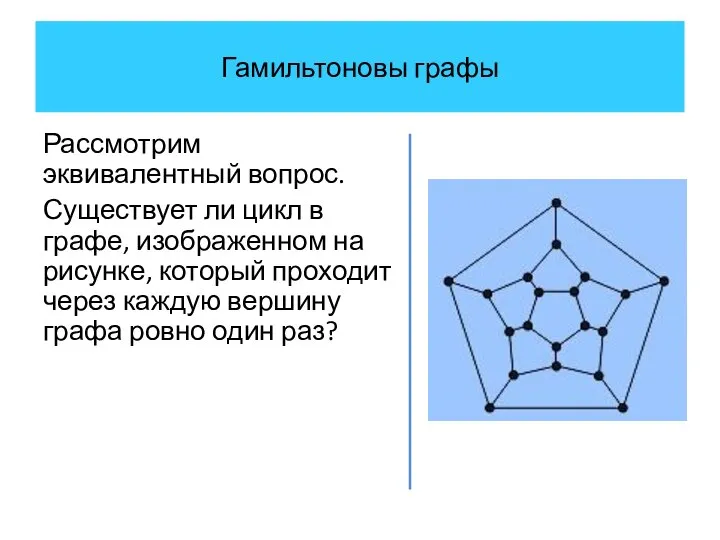
- 26. Гамильтоновы графы Рассмотрим эквивалентный вопрос. Существует ли цикл в графе, изображенном на рисунке, который проходит через
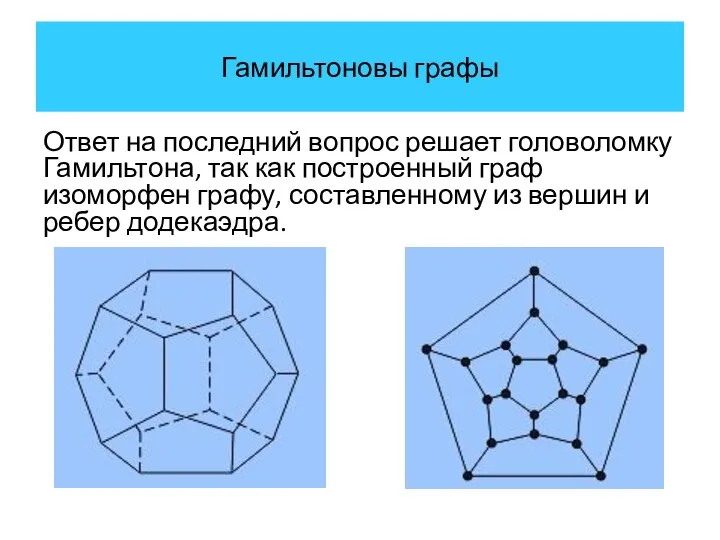
- 27. Гамильтоновы графы Ответ на последний вопрос решает головоломку Гамильтона, так как построенный граф изоморфен графу, составленному
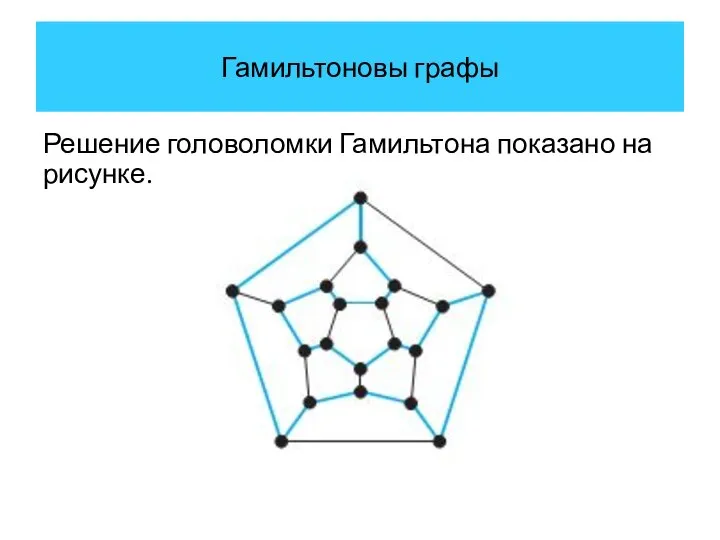
- 28. Гамильтоновы графы Решение головоломки Гамильтона показано на рисунке.
- 29. Гамильтоновы графы
- 30. Гамильтоновы графы Для эйлеровых графов имеется достаточно простой критерий. Однако, не так обстоят дела с гамильтоновыми
- 31. Гамильтоновы графы Эта задача остается одной из основных нерешенных проблем теории графов. Очевидным необходимым условием гамильтоновости
- 32. Гамильтоновы графы
- 33. Гамильтоновы графы
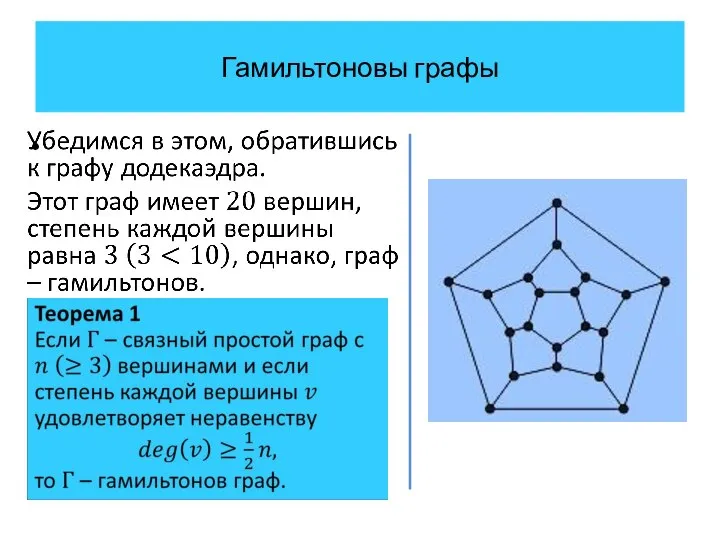
- 34. Гамильтоновы графы
- 35. Гамильтоновы графы В действительности, каждый из графов, связанных с пятью правильными многогранниками, имеет гамильтонов цикл.
- 36. Гамильтоновы графы
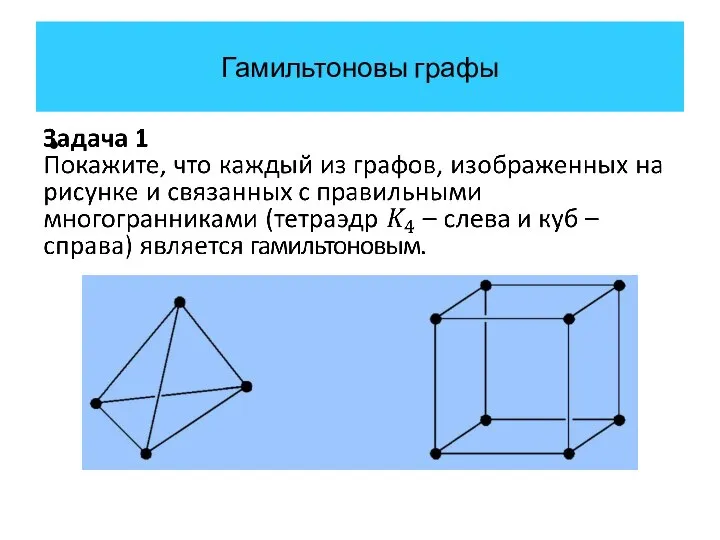
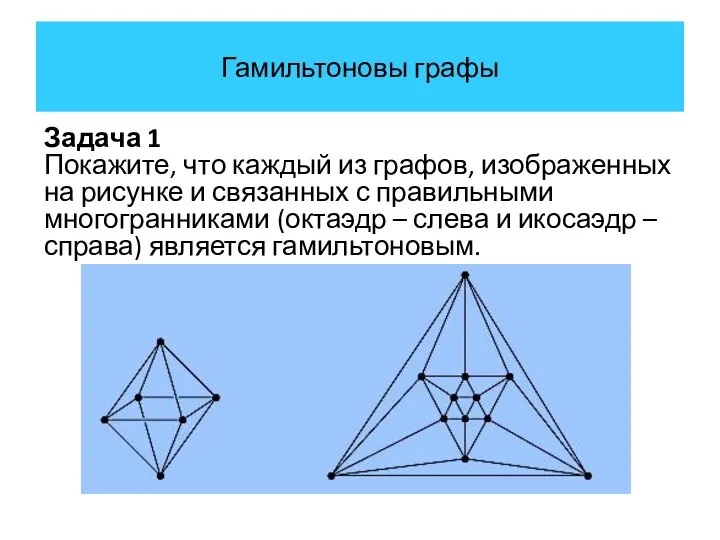
- 37. Гамильтоновы графы Задача 1 Покажите, что каждый из графов, изображенных на рисунке и связанных с правильными
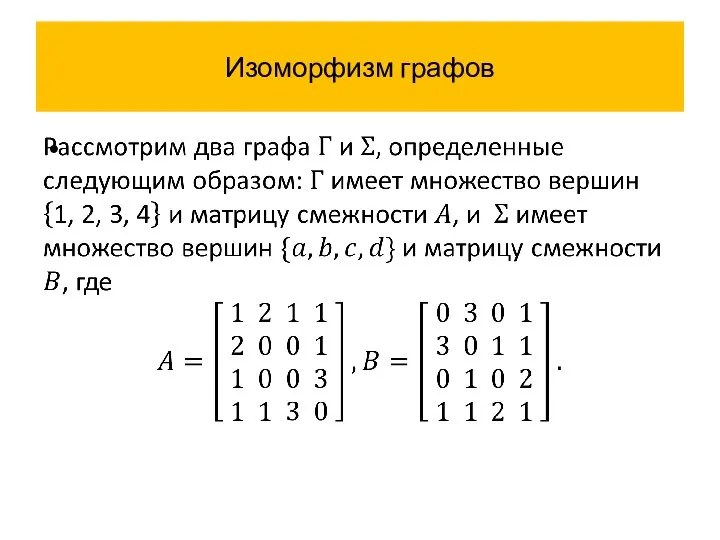
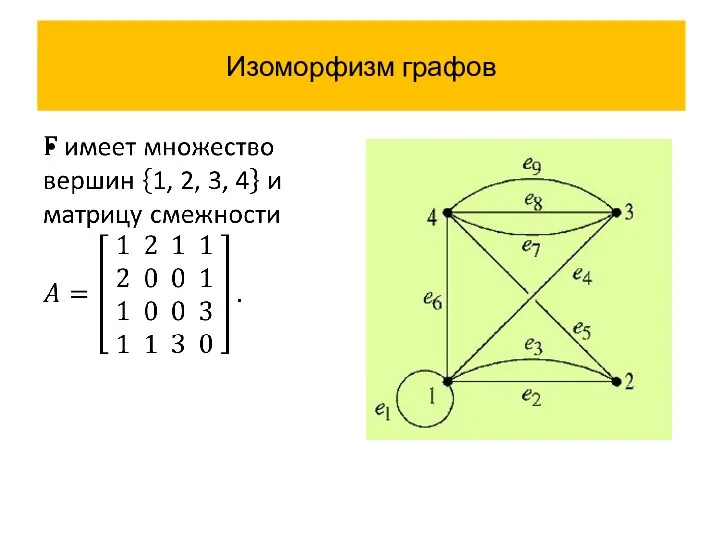
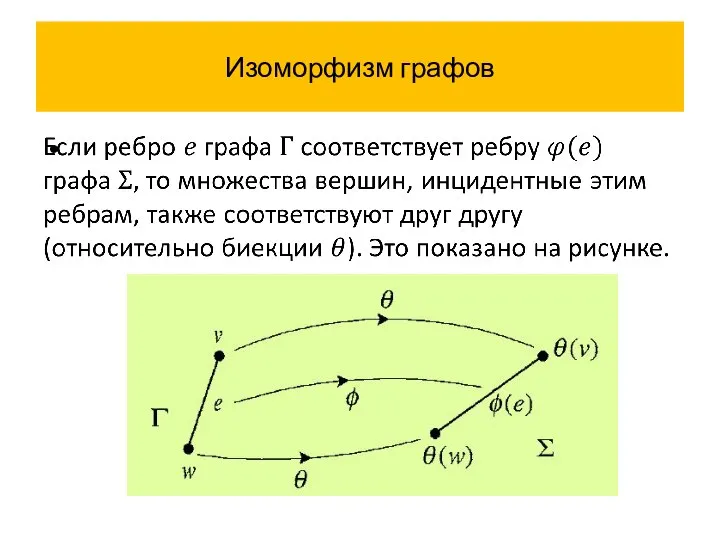
- 38. Изоморфизм графов
- 39. Изоморфизм графов
- 40. Изоморфизм графов
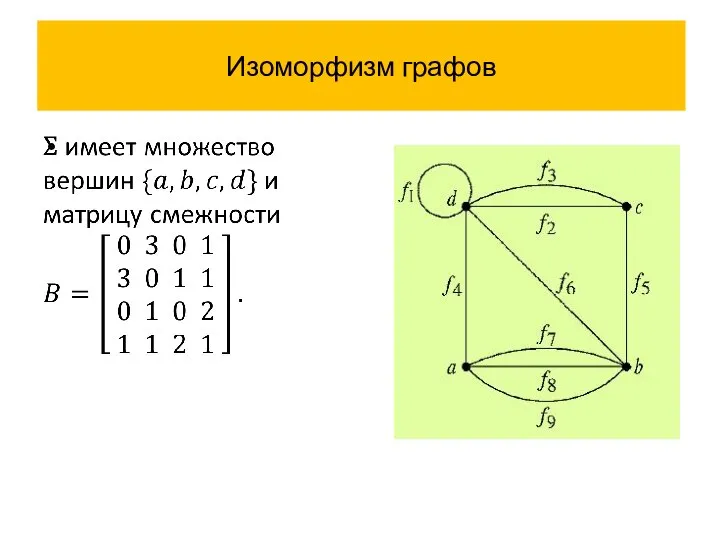
- 43. Изоморфизм графов
- 44. Изоморфизм графов
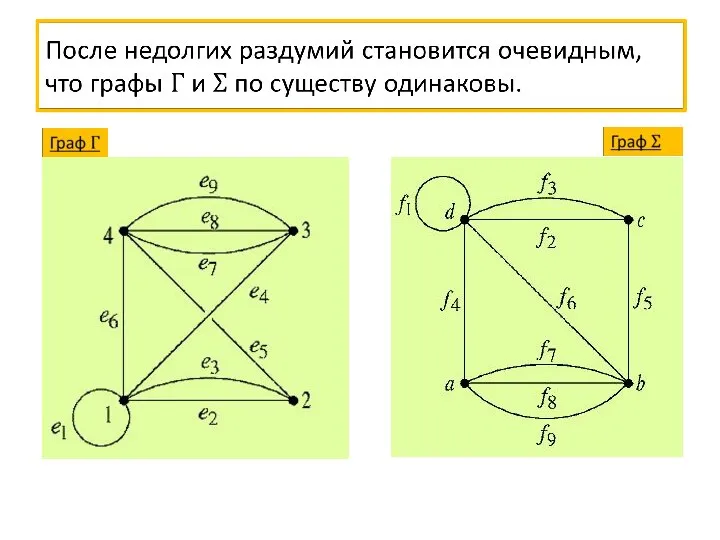
- 45. Изоморфизм графов
- 46. Изоморфизм графов
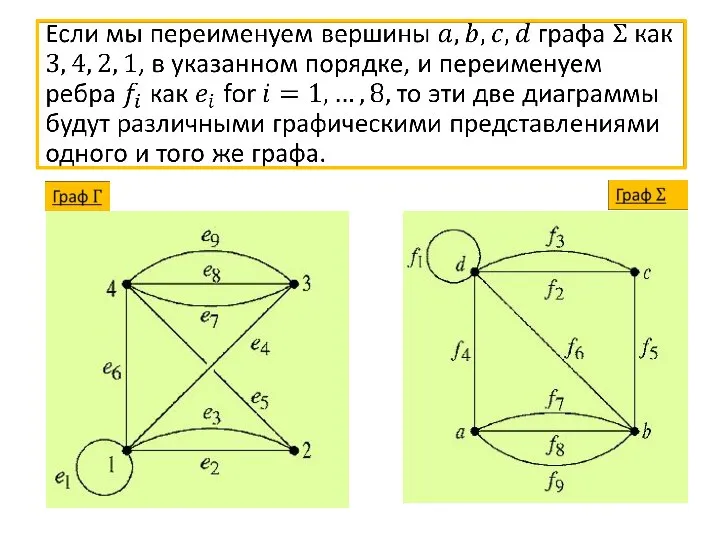
- 47. Изоморфизм графов
- 48. Изоморфизм графов Изоморфизм графов является отношением эквивалентности.
- 49. Изоморфизм графов Так как изоморфные графы имеют, по существу, одно и тоже строение, то любое теоретико-графовое
- 50. Изоморфизм графов
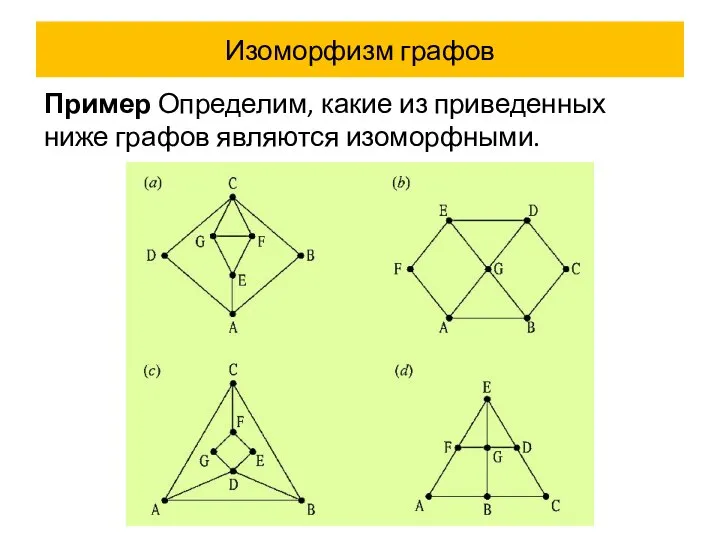
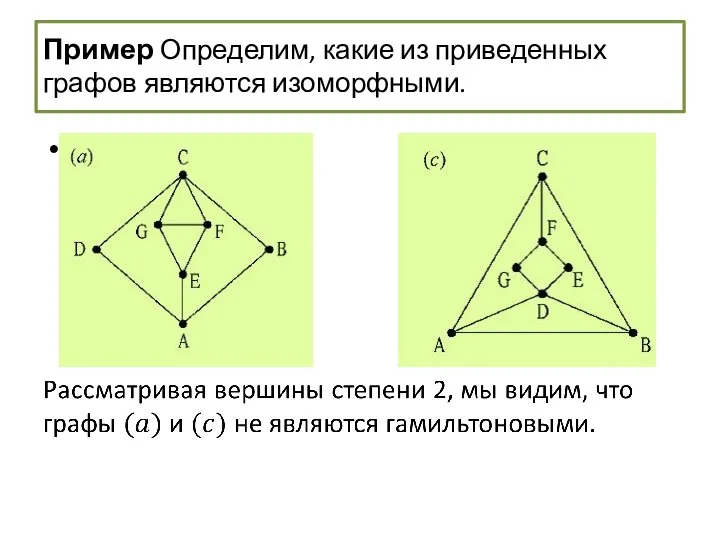
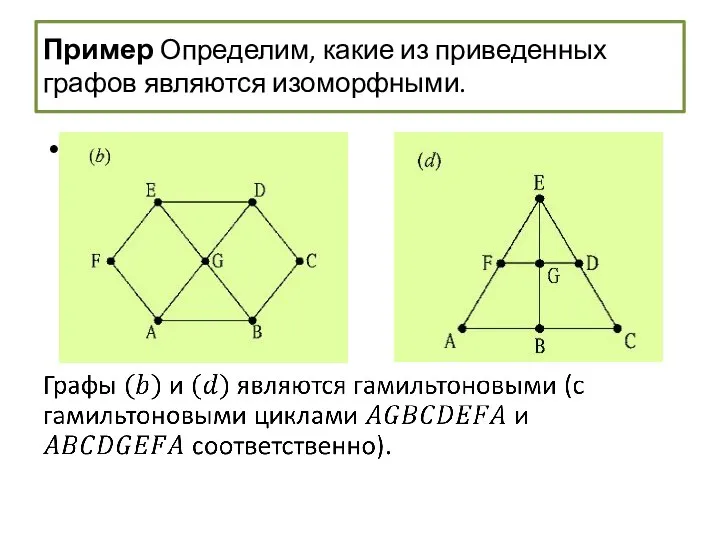
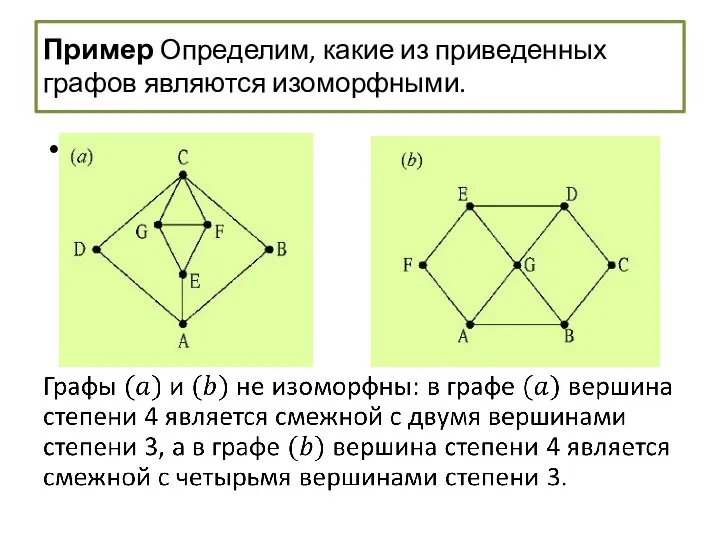
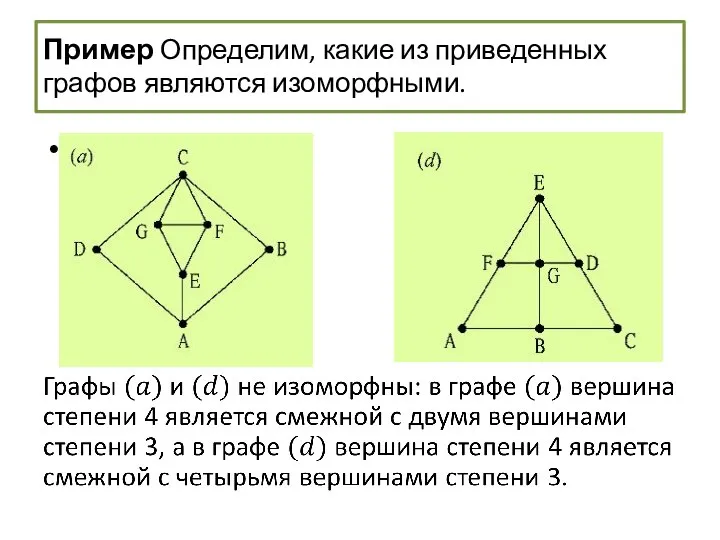
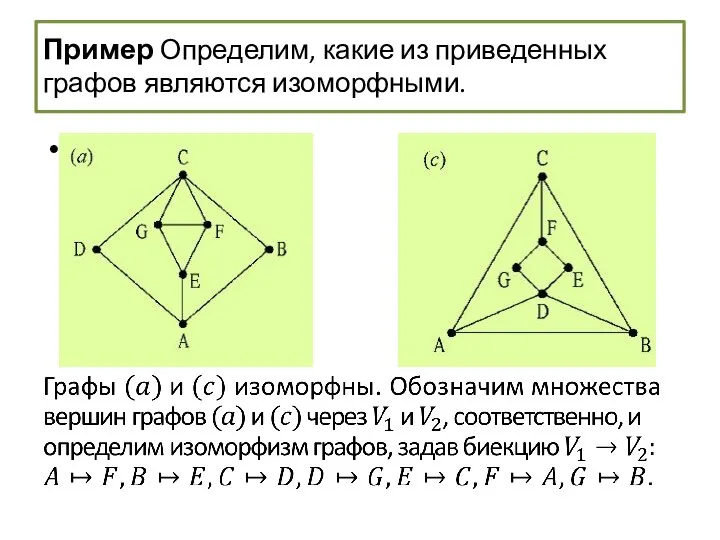
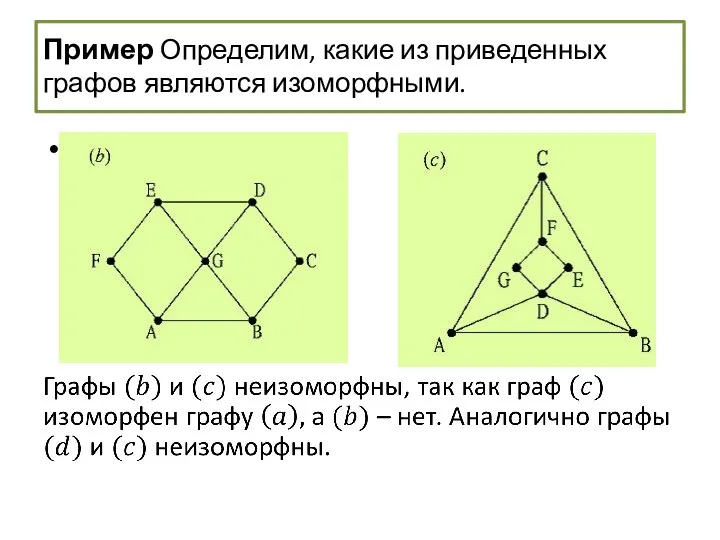
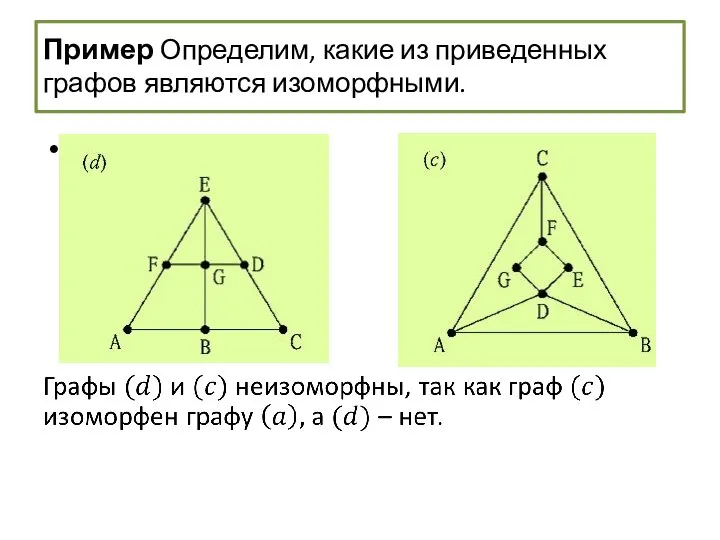
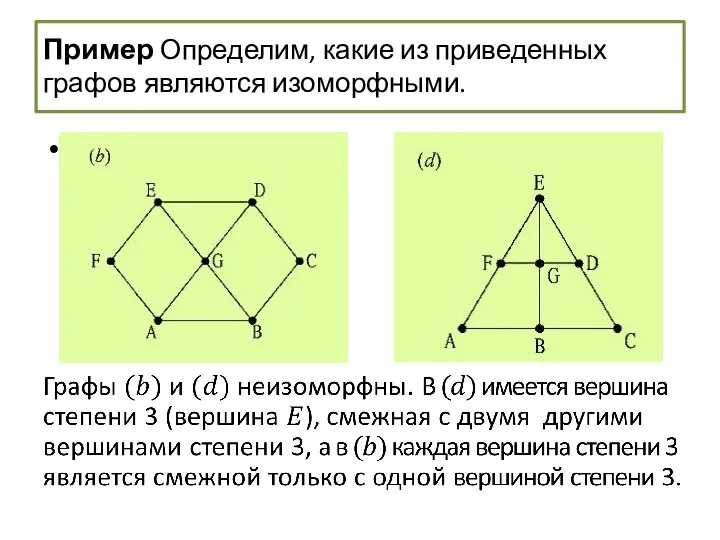
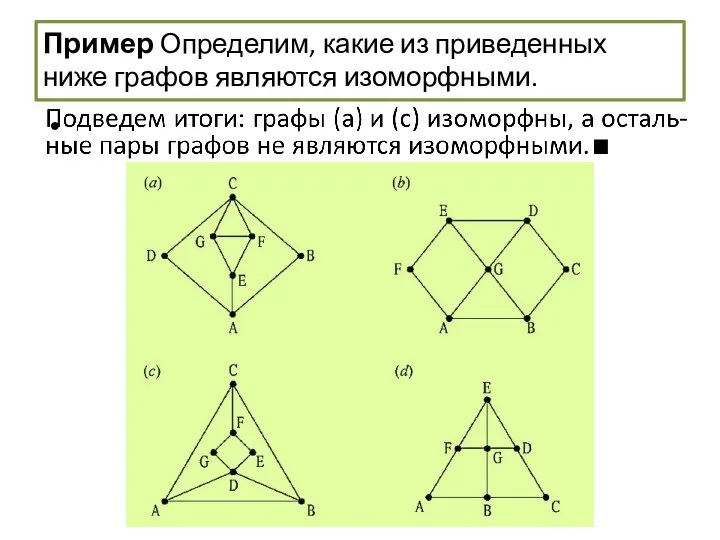
- 59. Изоморфизм графов Пример Определим, какие из приведенных ниже графов являются изоморфными.
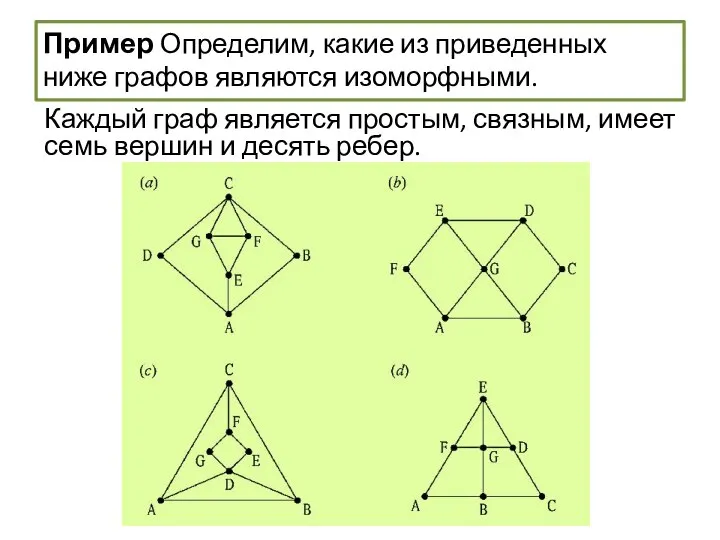
- 60. Пример Определим, какие из приведенных ниже графов являются изоморфными. Каждый граф является простым, связным, имеет семь
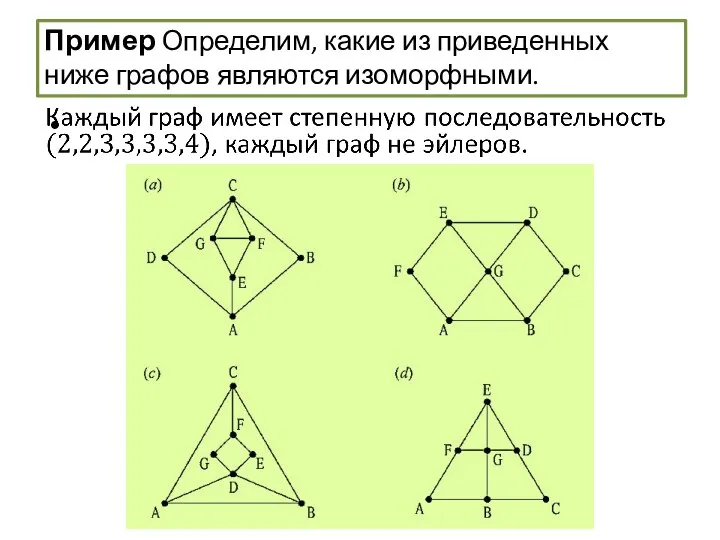
- 61. Пример Определим, какие из приведенных ниже графов являются изоморфными.
- 62. Пример Определим, какие из приведенных графов являются изоморфными.
- 63. Пример Определим, какие из приведенных графов являются изоморфными.
- 64. Пример Определим, какие из приведенных графов являются изоморфными.
- 65. Пример Определим, какие из приведенных графов являются изоморфными.
- 66. Пример Определим, какие из приведенных графов являются изоморфными.
- 67. Пример Определим, какие из приведенных графов являются изоморфными.
- 68. Пример Определим, какие из приведенных графов являются изоморфными.
- 69. Пример Определим, какие из приведенных графов являются изоморфными.
- 70. Пример Определим, какие из приведенных графов являются изоморфными.
- 71. Пример Определим, какие из приведенных ниже графов являются изоморфными.
- 73. Скачать презентацию

































 2 класс Математический диктант № 8 Выполнила Кирилова С.Г. Учитель начальных классов Школы «Ученики Пифагора» г. Лимассол, р.Кипр
2 класс Математический диктант № 8 Выполнила Кирилова С.Г. Учитель начальных классов Школы «Ученики Пифагора» г. Лимассол, р.Кипр Степень числа. 7 класс
Степень числа. 7 класс Презентация на тему Задачи на движение
Презентация на тему Задачи на движение  Модуль действительного числа
Модуль действительного числа Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Скалярное произведение векторов. Математический диктант
Скалярное произведение векторов. Математический диктант Презентация на тему Округление десятичных дробей
Презентация на тему Округление десятичных дробей  Елементи теорії виміру. Шкали виміру. Лекція 5. Тема 3
Елементи теорії виміру. Шкали виміру. Лекція 5. Тема 3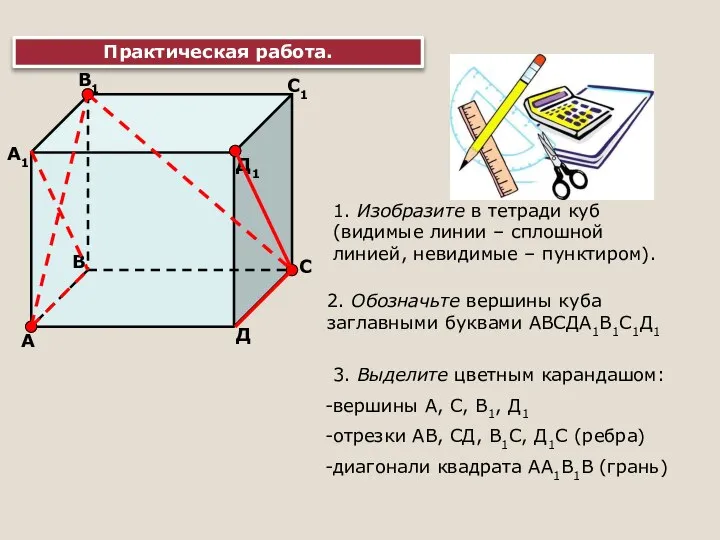 Решение задач по стереометрии
Решение задач по стереометрии Правила выполнения действий с натуральными числами
Правила выполнения действий с натуральными числами График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными ГИА - 2012. Открытый банк заданий по математике. (Задача 4)
ГИА - 2012. Открытый банк заданий по математике. (Задача 4) Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Делимость натуральных чисел
Делимость натуральных чисел Ромб. Свойства параллелограмма
Ромб. Свойства параллелограмма Планиметрия
Планиметрия Запись всех точек, соответствующих данным точкам единичной окружности
Запись всех точек, соответствующих данным точкам единичной окружности Сумма n-первых членов арифметической прогрессии
Сумма n-первых членов арифметической прогрессии Иррациональные уравнения и неравенства
Иррациональные уравнения и неравенства Формулы двойного аргумента
Формулы двойного аргумента Женщины в математике
Женщины в математике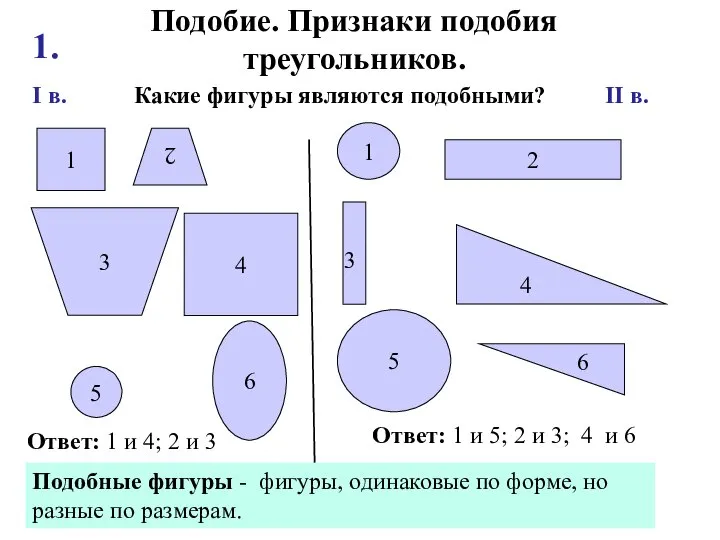 Подобие. Признаки подобия треугольников
Подобие. Признаки подобия треугольников Обыкновенные дроби
Обыкновенные дроби Презентация на тему Сумма углов треугольника
Презентация на тему Сумма углов треугольника  Муниципальное бюджетное образовательное учреждение «Лопхаринская средняя общеобразовательная школа» Урок математики в 5 кла
Муниципальное бюджетное образовательное учреждение «Лопхаринская средняя общеобразовательная школа» Урок математики в 5 кла Сумма углов треугольника
Сумма углов треугольника Кубик Рубика - гимнастика ума. Исследовательская работа
Кубик Рубика - гимнастика ума. Исследовательская работа Задачи оптимизации производства товаров и услуг
Задачи оптимизации производства товаров и услуг