Содержание
- 2. 9.1 Классификация игр. Антагонистические игры.
- 7. Таким образом, в игровых задачах всегда известен набор стратегий (вариантов решений), доступный ЛПР. В качестве единственного
- 9. Кроме игр с нулевой и ненулевой суммой в которых участвуют не менее двух игроков, преследующих собственные
- 14. Пусть имеются два игрока - А и B, каждый из которых может выбрать одну из трех
- 43. 9.2 Биматричные игры
- 44. Биматричные игры – это игры с ненулевой суммой общего выигрыша, происходящие между двумя игроками, каждый из
- 45. В зависимости от того, разрешено или запрещено сотрудничество игроков, биматричные игры делятся на некооперативные и кооперативные.
- 46. В некооперативной игре при выборе стратегии игроки руководствуются принципом максимальной осторожности. Если условия игры позволяют смешивать
- 47. Рассмотрим в качестве примера некооперативной игры задачу «Дилемма заключенных». Двое преступников попали в тюрьму. Если оба
- 48. Согласно принципу максимальной осторожности в некооперативной игре оба игрока должны сознаться. Данное решение является точкой равновесия
- 49. Выбранные стратегии игроков образуют равновесие Нэша, если ни одному из игроков не выгодно отклоняться от равновесной
- 50. Пример. Рассмотрим в качестве примера игру «студент-преподаватель». Студент (игрок A) готовиться к зачету, который принимает преподаватель
- 51. Решение. Во-первых, рассмотрим действия игроков, продиктованные принципом максимальной осторожности, т.е. поместим их в условия, когда им
- 52. Отметим, что поскольку верхняя и нижняя цена игры для матрицы выигрышей преподавателя не совпадают, он может
- 53. Легко проверить, что равновесие по Нэшу в этой задаче обеспечивают наборы чистых стратегий (A1, B1) с
- 54. В кооперативных играх игрокам разрешено договариваться друг с другом. Вместе с тем, ни один игрок не
- 55. В кооперативной задаче о заключенных переговорное множество образуют решения (-8, -8) и (-1, -1). Поскольку второе
- 56. Если переговорное множество состоит из парето-оптимальных решений (доминирующих решений нет) и договориться о выборе той или
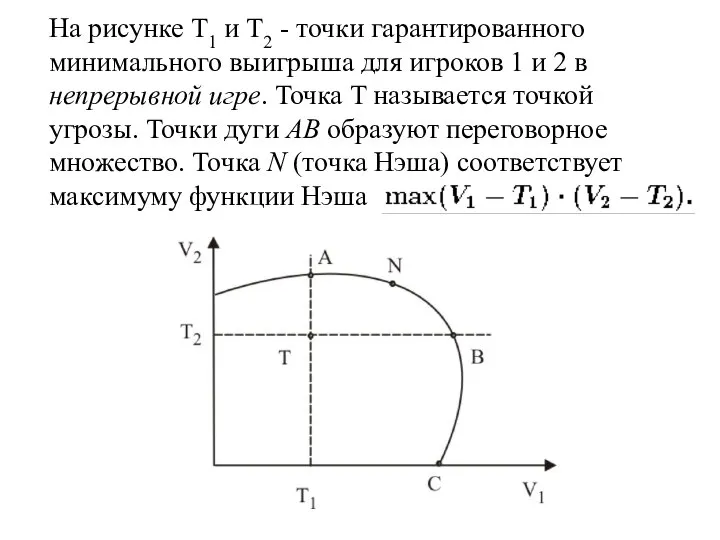
- 57. На рисунке T1 и T2 - точки гарантированного минимального выигрыша для игроков 1 и 2 в
- 58. В теории игр доказано, что если множество возможных выигрышей выпукло, замкнуто и ограничено сверху, то точка
- 59. Принцип Нэша можно применить и для решения биматричных игр. Просто здесь множество возможных решений ограничено несколькими
- 61. Чтобы найти решение, максимизирующее функцию Нэша f(x,y)=max(x-4)(y-4), выразим y через x, записав уравнение прямой AD (y-8)/(8-2)=(x-2)/(2-8),
- 62. В данной игре кооперация будет выгодна обоим игрокам только при условии, что они смогут поделить суммарный
- 63. В общем случае, решение биматричной игры может основываться на различных критериях, среди которых: 1. Стремление каждого
- 66. 9.3 Игры с природой
- 108. 9.4 Позиционные игры
- 109. В отличие от рассмотренных ранее игр позиционная игра моделирует процесс последовательного принятия решений ее участниками. Игра
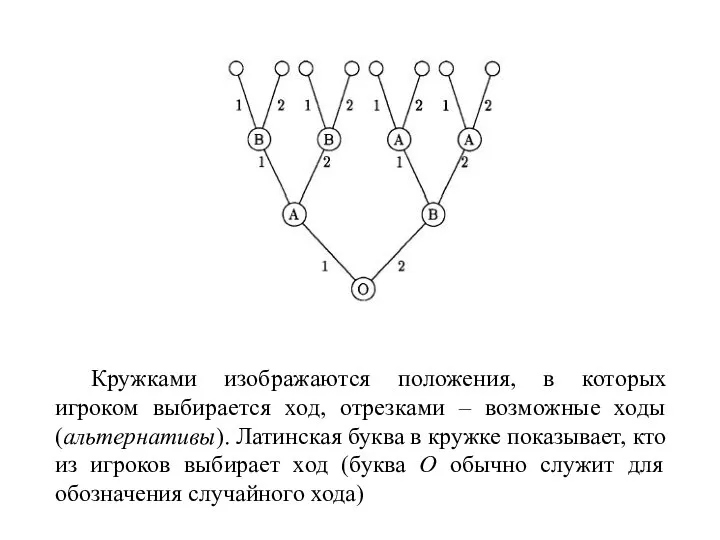
- 110. Кружками изображаются положения, в которых игроком выбирается ход, отрезками – возможные ходы (альтернативы). Латинская буква в
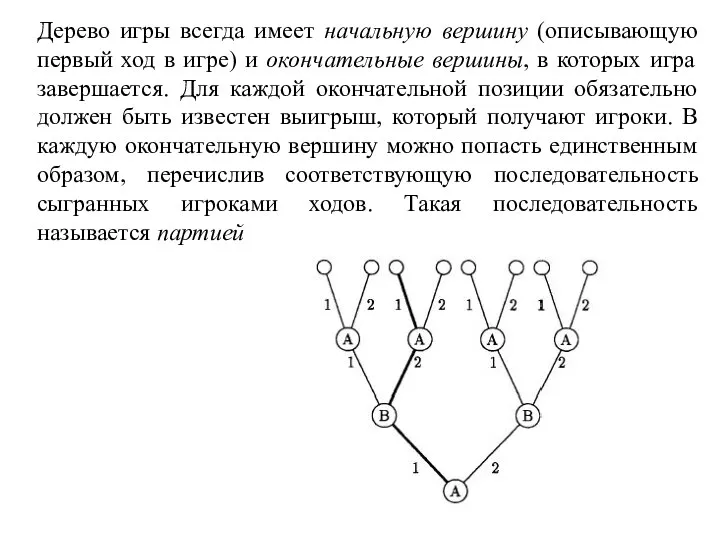
- 111. Дерево игры всегда имеет начальную вершину (описывающую первый ход в игре) и окончательные вершины, в которых
- 112. Нормальная форма позиционной игры Все игры, которые мы рассматривали ранее, были представлены в так называемой, «нормальной
- 113. Пример. Пусть имеется два игрока, причем у каждого есть всего две стратегии – назвать число 1
- 114. В рассмотренном примере мы построили нормальную форму для антагонистической игры с матрицей выигрышей: Решением игры являются
- 115. Двухходовая позиционная игра с неполной информацией. Используя данные рассмотренного примера, попробуем построить позиционную игру (с последовательными
- 116. Как уже говорилось, все позиционные игры можно разделить на игры с полной и неполной информацией. Предположим,
- 117. Пунктиром на этом рисунке выделены информационные множества игроков A и B. Информационное множество игрока в позиционной
- 118. Очевидно , что игрок А, совершая ход, может выбрать одну из двух стратегий {A1: x=1, A2:
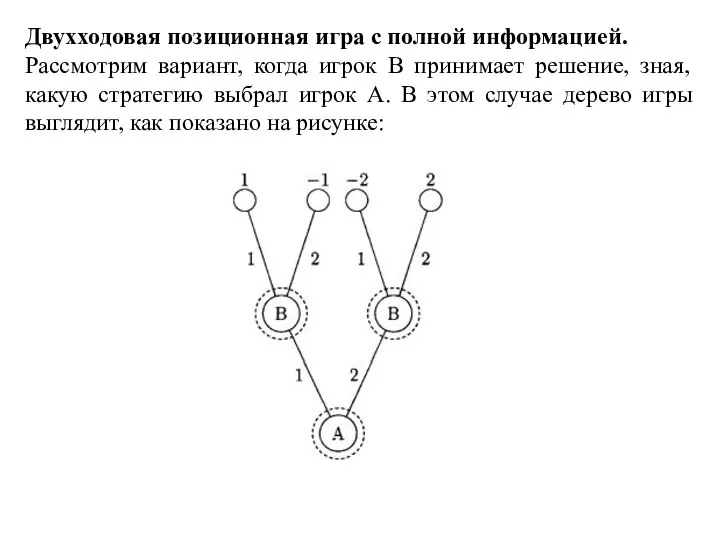
- 119. Двухходовая позиционная игра с полной информацией. Рассмотрим вариант, когда игрок B принимает решение, зная, какую стратегию
- 120. Игрок A по-прежнему имеет те же две стратегии {A1: x=1, A2: x=2}. Однако с игроком B
- 121. Так, стратегия [1, 1] означает, что независимо от хода игрока A игрок B назовет 1, а
- 122. Результирующую матрицу выплат можно представить в следующем виде: С учетом конкретных значений W (x, y1(2)) получим
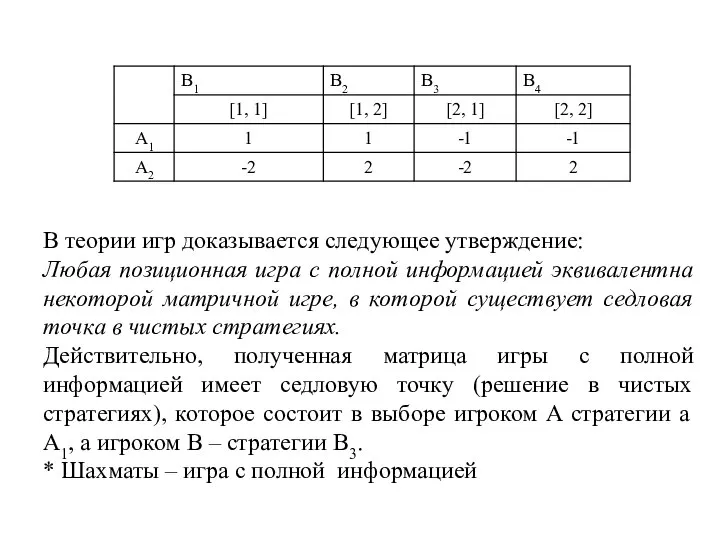
- 123. В теории игр доказывается следующее утверждение: Любая позиционная игра с полной информацией эквивалентна некоторой матричной игре,
- 124. Позиционная игра в три хода с полной информацией. Рассмотрим вариант игры с полной информацией, в которой
- 125. Обозначим переменными x и z выбор игрока A на первом и третьем ходу, а переменной y
- 126. Рассмотрим сначала возможные действия игрока B. С точки зрения его возможных стратегий игра ничем не отличается
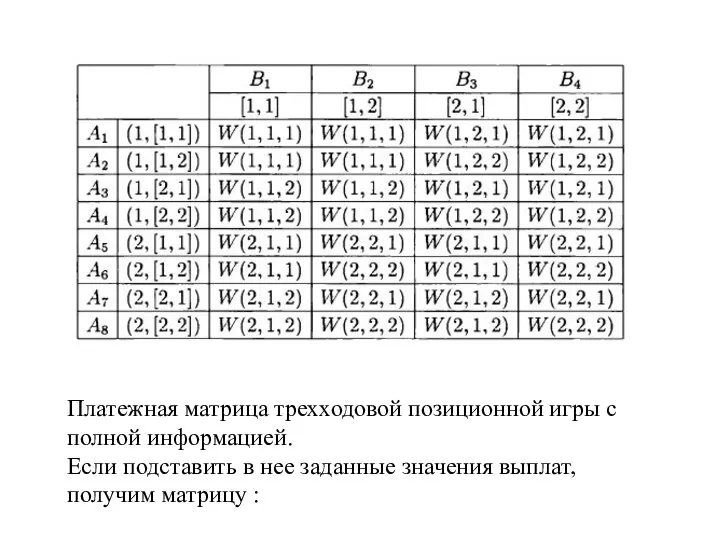
- 127. Платежная матрица трехходовой позиционной игры с полной информацией. Если подставить в нее заданные значения выплат, получим
- 129. Позиционная игра в три хода с неполной информацией. Пусть в описанной выше игре в три хода
- 131. Вариант 2. Пусть игрок A на третьем этапе игры по-прежнему не помнит своего первого хода и
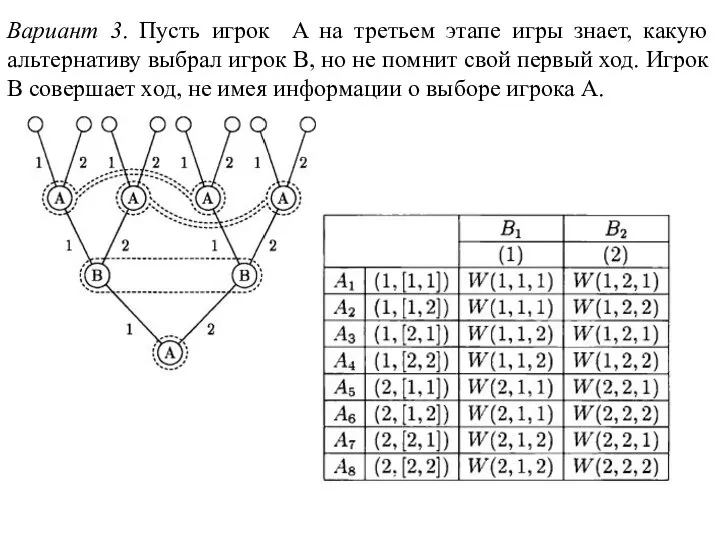
- 132. Вариант 3. Пусть игрок A на третьем этапе игры знает, какую альтернативу выбрал игрок B, но
- 133. Позиционная игра в три хода с неполной информацией и случайным выбором первого хода. Пусть первый ход
- 136. Если учесть вероятности выбора альтернатив на первом ходу (p1=0.5 и p2=0.5), можно построить результирующую платежную матрицу,
- 138. Скачать презентацию



















































































































![Так, стратегия [1, 1] означает, что независимо от хода игрока A](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1444012/slide-120.jpg)












 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Числовые ряды
Числовые ряды Понятие действительного числа
Понятие действительного числа Презентация по математике "Круглые тела: цилиндр, конус, шар" - скачать бесплатно
Презентация по математике "Круглые тела: цилиндр, конус, шар" - скачать бесплатно Свойства дисперсии
Свойства дисперсии Симметрия в пространстве
Симметрия в пространстве Математика 1 класс Развивающая система Л.В.Занкова Тема: Число и цифра 8 Составила и провела:
Математика 1 класс Развивающая система Л.В.Занкова Тема: Число и цифра 8 Составила и провела:  Какие числовые множества Вам знакомы?
Какие числовые множества Вам знакомы? Касательная и нормаль к графику
Касательная и нормаль к графику Многоугольники. Признаки параллелограмма
Многоугольники. Признаки параллелограмма Применение распределительного свойства умножения 6 класс
Применение распределительного свойства умножения 6 класс  Теорема Пифагора. Применение теоремы в ходе решения задач
Теорема Пифагора. Применение теоремы в ходе решения задач Тренажер Таблица умножения трёх
Тренажер Таблица умножения трёх Алгоритм решения базовых задач
Алгоритм решения базовых задач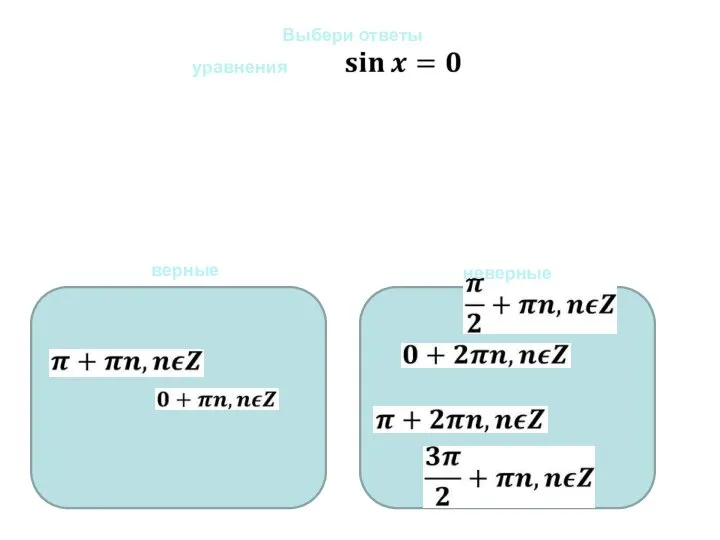 Уравнения sinx=0, cosx=0. Выберите правильный ответ
Уравнения sinx=0, cosx=0. Выберите правильный ответ Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Линейная функция. 7 класс
Линейная функция. 7 класс Применение векторов к решению задач. Геометрия (9 класс)
Применение векторов к решению задач. Геометрия (9 класс) Схема Бернулли
Схема Бернулли Длина окружности. Коллекция задач для 6 класса
Длина окружности. Коллекция задач для 6 класса Конус. Решение задач
Конус. Решение задач УРОК ПО МАТЕМАТИКЕ В 1 КЛАССЕ УЧИТЕЛЬ РЫБАЛКА А.В. ВЛАДИКАВКАЗ 2010-2011 Слагаемые, сумма .
УРОК ПО МАТЕМАТИКЕ В 1 КЛАССЕ УЧИТЕЛЬ РЫБАЛКА А.В. ВЛАДИКАВКАЗ 2010-2011 Слагаемые, сумма . Аттестационная работа. Значение включения в программу занятий со школьниками материала, освоенного в рамках курсов
Аттестационная работа. Значение включения в программу занятий со школьниками материала, освоенного в рамках курсов Геометричні перетворення графіків функцій
Геометричні перетворення графіків функцій Своя игра. Дроби десятичные и обыкновенные. Игра для развития серых клеточек
Своя игра. Дроби десятичные и обыкновенные. Игра для развития серых клеточек Умножение одночлена на многочлен
Умножение одночлена на многочлен Лекция 7. Постановка задачи нелинейного программирования. Теорема Куна-Таккера
Лекция 7. Постановка задачи нелинейного программирования. Теорема Куна-Таккера Презентация по математике "Ассоциация, как помощник, при изучении математики" - скачать
Презентация по математике "Ассоциация, как помощник, при изучении математики" - скачать