Замена переменной
позволяет получить интеграл от
рациональной функции. Интеграл(1) примет вид
Замечание
Интеграл вида
вычисляется с помощью
замены
Биноминальный дифференциал – это выражение вида
, где
Теорема Чебышева
Интеграл
(1) может быть выражен в элементарных функциях
только в следующих трех случаях:
1) p – целое число. Тогда выражение
развертывается по формуле
, которые легко интегрируются.
бинома Ньютона и подынтегральная функция после раскрытия скобок будет суммой элементов вида
2) целое число. Интеграл (1) приводится к интегралу от
рациональной функции подстановкой
, где r – знаменатель дроби p
3) целое число. Интеграл (1) приводится к интегралу от
рациональной функции подстановкой
, где r – знаменатель
дроби p.






 Таблица сложения и вычитания с числом 4
Таблица сложения и вычитания с числом 4 ЕГЭ профильная математика. Задание № 1. ЕГЭ базовая математика. Задание № 6
ЕГЭ профильная математика. Задание № 1. ЕГЭ базовая математика. Задание № 6 Задачи о земледелии в горных районах. Решение практико - ориентированных задач
Задачи о земледелии в горных районах. Решение практико - ориентированных задач Таблиця множення числа 4
Таблиця множення числа 4 Линейная функция и ее график. 7 класс
Линейная функция и ее график. 7 класс Многогранники. Призма
Многогранники. Призма Соотношения между углами и сторонами прямоугольного треугольника
Соотношения между углами и сторонами прямоугольного треугольника Математическая статистика (лекция 5)
Математическая статистика (лекция 5) Наименьшее общее кратное и наибольший общий делитель
Наименьшее общее кратное и наибольший общий делитель Решение линейных уравнений с параметром и модулем
Решение линейных уравнений с параметром и модулем Значение степени возведение в степень
Значение степени возведение в степень Гамильтоновы циклы
Гамильтоновы циклы Алгоритм сложения (вычитания) десятичных дробей
Алгоритм сложения (вычитания) десятичных дробей Презентация по математике "Красоту человека поможет вычислить «Божественная пропорция»" - скачать
Презентация по математике "Красоту человека поможет вычислить «Божественная пропорция»" - скачать  Логика предикатов
Логика предикатов Квадратные уравнения
Квадратные уравнения Оболонки додатної і відʼємної Гаусової кривизни
Оболонки додатної і відʼємної Гаусової кривизни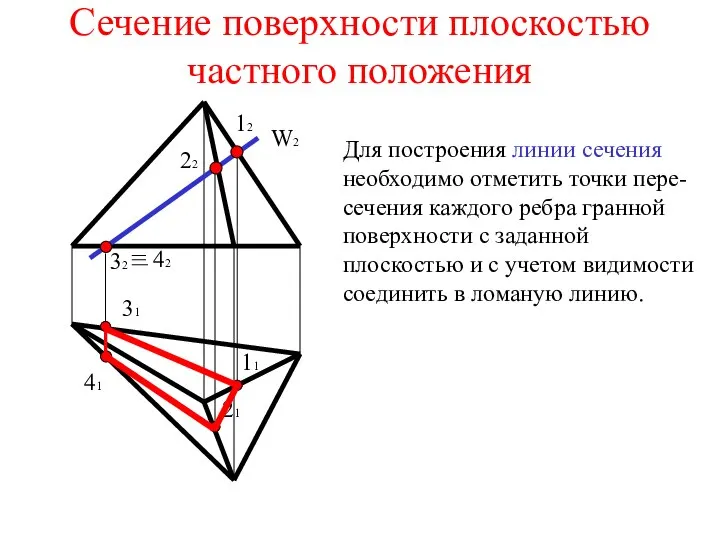 Сечение поверхности плоскостью частного положения
Сечение поверхности плоскостью частного положения Исторические задачи по математике
Исторические задачи по математике Все действия с десятичными дробями. Повторение. 6 класс
Все действия с десятичными дробями. Повторение. 6 класс Математические диктанты. (3 класс)
Математические диктанты. (3 класс) Методы измерения. Измерительные приборы. 5 кл
Методы измерения. Измерительные приборы. 5 кл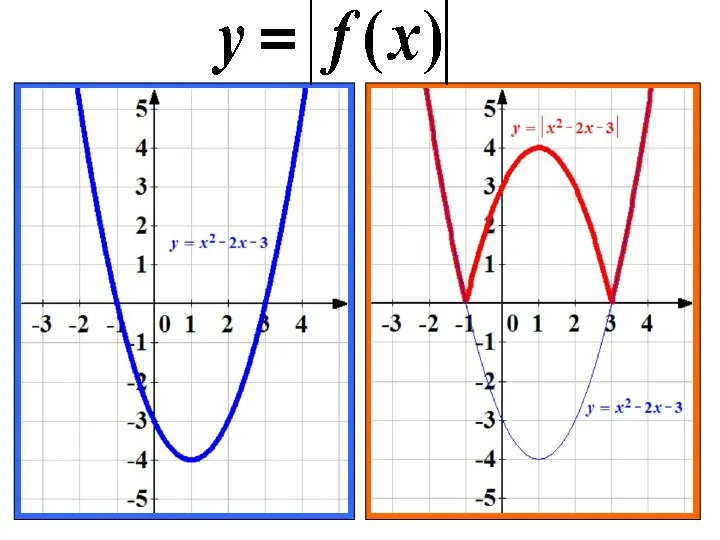 Построение графика функции y f (x )
Построение графика функции y f (x ) Методика формирования математических понятий у учащихся 5 – 6 классов
Методика формирования математических понятий у учащихся 5 – 6 классов Несобственные интегралы
Несобственные интегралы Рационал сандарды азайту. Координаталық түзудегі кесіндінің ұзындығы
Рационал сандарды азайту. Координаталық түзудегі кесіндінің ұзындығы Қосынды және айырым түрінде берілген тригонометриялық функцияларды көбейтінді түріне келтіру
Қосынды және айырым түрінде берілген тригонометриялық функцияларды көбейтінді түріне келтіру МАТЕМАТИКА-ЦАРИЦА НАУК? ВЫПОЛНИЛ ученик 9-го класса Муравский Владимир. Учитель: Матусова М.Н.
МАТЕМАТИКА-ЦАРИЦА НАУК? ВЫПОЛНИЛ ученик 9-го класса Муравский Владимир. Учитель: Матусова М.Н.