Содержание
- 2. Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств
- 3. ? Для поддержки принятия решений в медицине и экономике. ? В автомобильной, аэрокосмической и транспортной промышленности,
- 4. Характеристикой нечеткого множества выступает функция принадлежности (Membership Function). Обозначим через MFc(x) – степень принадлежности к нечеткому
- 5. Формализуем неточное определение 'горячий чай'. В качестве x (область рассуждений) будет выступать шкала температуры в градусах
- 6. Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчетов,
- 7. В теории нечетких множеств разработан общий подход к выполнению операторов пересечения, объединения и дополнения, реализованный в
- 8. Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных. Нечеткая переменная описывается набором (N,X,A), где
- 9. Каждая лингвистическая переменная состоит из: • Названия; • Множества своих значений, которое также называется базовым терм-множеством
- 10. Рассмотрим нечеткое понятие 'Цена акции'. Это и есть название лингвистической переменной. Сформируем для нее базовое терм-множество,
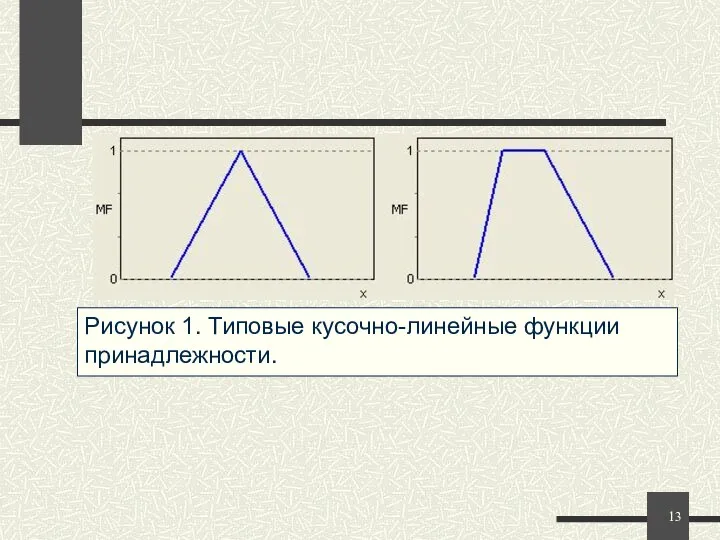
- 11. Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:
- 12. Для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d): При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный
- 13. Рисунок 1. Типовые кусочно-линейные функции принадлежности. При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.
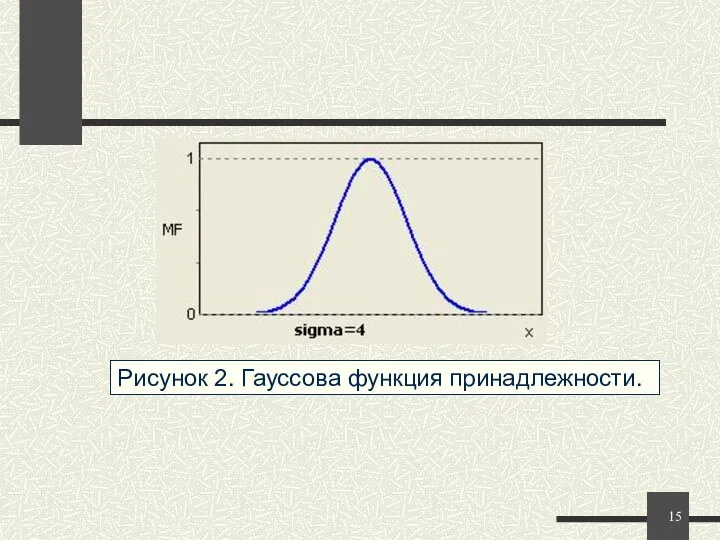
- 14. Функция принадлежности гауссова типа описывается формулой: и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества,
- 15. Рисунок 2. Гауссова функция принадлежности. При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.
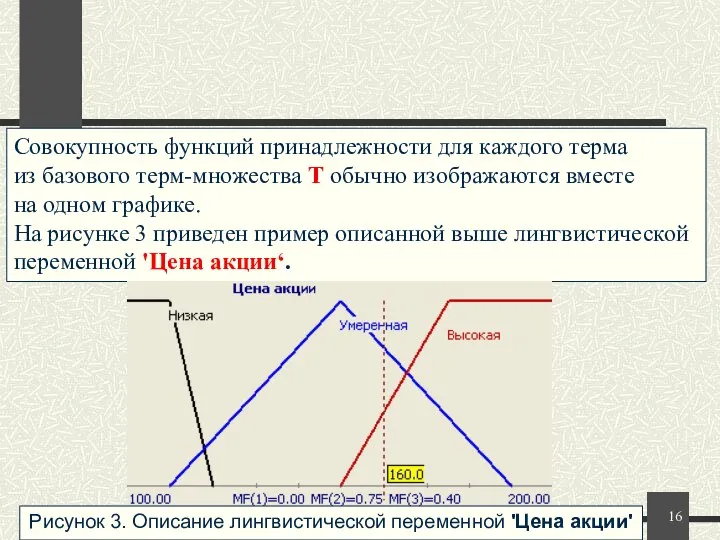
- 16. Совокупность функций принадлежности для каждого терма из базового терм-множества T обычно изображаются вместе на одном графике.
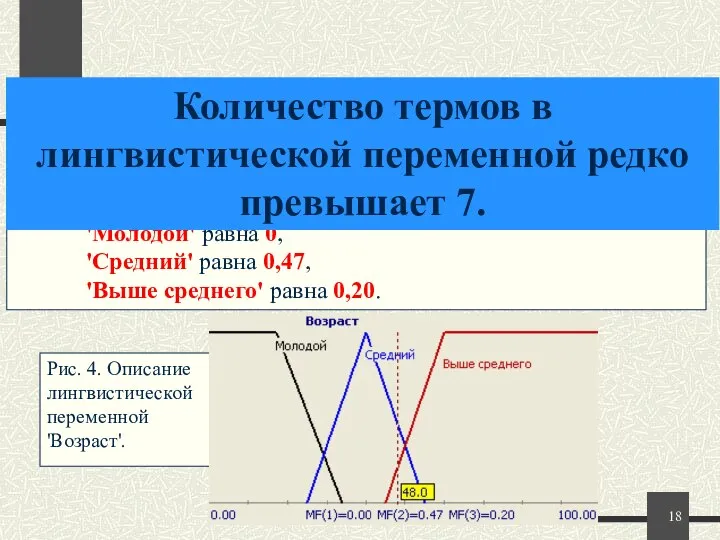
- 17. На рисунке 4 представлена формализация неточного понятия 'Возраст человека'. Так, для человека 48 лет степень принадлежности
- 18. На рисунке 4 представлена формализация неточного понятия 'Возраст человека'. Так, для человека 48 лет степень принадлежности
- 19. Основой для проведения операции нечеткого логического вывода является база правил, содержащая нечеткие высказывания в форме 'Если-то'
- 20. Пусть в базе правил имеется m правил вида: R1: ЕСЛИ x1 это A11 … И …
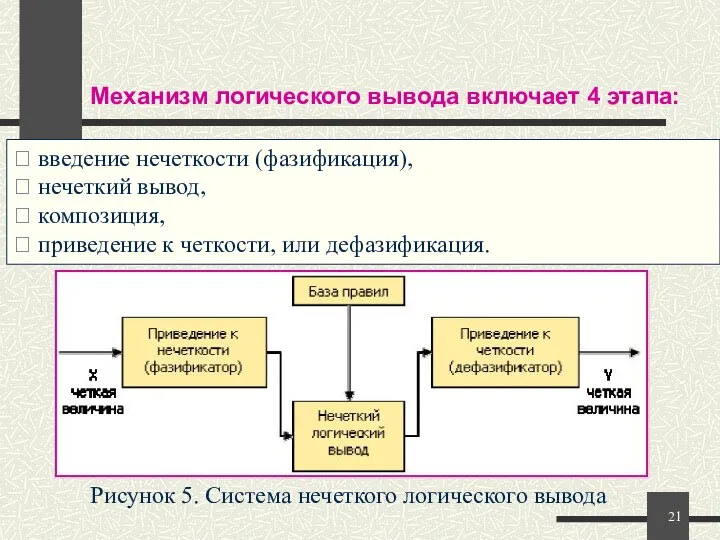
- 21. ? введение нечеткости (фазификация), ? нечеткий вывод, ? композиция, ? приведение к четкости, или дефазификация. Механизм
- 22. Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны
- 24. Скачать презентацию
















 Решение уравнения cosx = a. Понятие арккосинуса числа
Решение уравнения cosx = a. Понятие арккосинуса числа Урок - морское путешествие
Урок - морское путешествие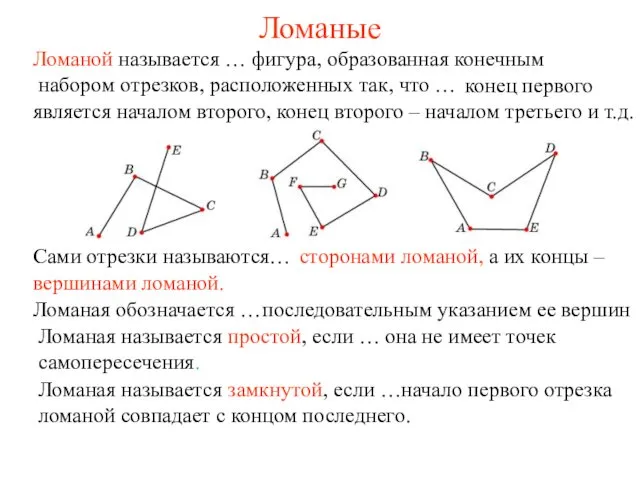 Ломаные и многоугольники
Ломаные и многоугольники Одночлен. 7 класс
Одночлен. 7 класс Вычисления с рациональными числами
Вычисления с рациональными числами Преобразования графиков тригонометрических функций с модулем
Преобразования графиков тригонометрических функций с модулем Презентация по математике "О математическом языке" - скачать бесплатно
Презентация по математике "О математическом языке" - скачать бесплатно Выборочное наблюдение
Выборочное наблюдение Тема урока
Тема урока  Решение задач с практическим содержанием
Решение задач с практическим содержанием Векторна алгебра
Векторна алгебра Доли
Доли Это страшное слово: «Параметр»
Это страшное слово: «Параметр» Путешествие в страну обыкновенных дробей
Путешествие в страну обыкновенных дробей Логика. Доказательство и опровержение
Логика. Доказательство и опровержение Муниципальное бюджетное общеобразовательное учреждение гимназия №1 г. Североморск
Муниципальное бюджетное общеобразовательное учреждение гимназия №1 г. Североморск  Математические бои
Математические бои Методы математической статистики в психологопедагогических исследованиях
Методы математической статистики в психологопедагогических исследованиях Многоугольники
Многоугольники Квадратичная функция. Преобразование графика параболы путем параллельного переноса вдоль осей абцисс и ординат
Квадратичная функция. Преобразование графика параболы путем параллельного переноса вдоль осей абцисс и ординат Прямоугольник. Урок математики. 2 класс
Прямоугольник. Урок математики. 2 класс Решение треугольников
Решение треугольников Подобные треугольники. Подобные фигуры
Подобные треугольники. Подобные фигуры Свойства числовых неравенств
Свойства числовых неравенств Случаи сложения и вычитания, основанные на знании нумерации чиселм
Случаи сложения и вычитания, основанные на знании нумерации чиселм Тест по теме: "Пирамида". Часть 2. Вариант 2
Тест по теме: "Пирамида". Часть 2. Вариант 2 Функции нескольких переменных. Частные производные
Функции нескольких переменных. Частные производные Параллельность прямой и плоскости. Решение задач
Параллельность прямой и плоскости. Решение задач