Из истории интересных чисел. Число П

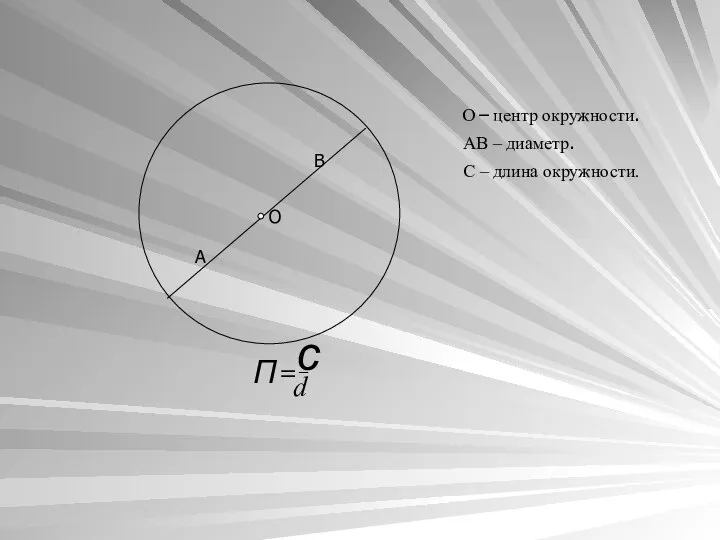
Слайд 4

А
В
О
О – центр окружности.
АВ – диаметр.
С – длина окружности.
П=
с
_
d

Слайд 5

π — иррациональное число, то есть его значение не может быть

точно выражено в виде дроби m/n, где m и n — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим.

Слайд 6

В глубокой древности считалось, что окружность ровно 3 раза длиннее диаметра.

Эти сведения содержатся в клинописных табличках Древнего Междуречья. Такое же значение можно извлечь из текста Библии: « И сделал литое из меди море, - от края его до края его десять локтей, -совсем круглое… и снурок в тридцать локтей обнимал его кругом» ( 3 Цар. 7. 23). Итак, первым приближением числа П было 3.

Вычисления числа П

Слайд 7

Слайд 8

Важным достижением в вычислении числа П было очень хорошее приближение числа

П древних египтян. Оно получается из формулы для площади круга диаметра d:
S=(d – 1/9) = (1 – 1/9) d
Этому правилу из 50-й задачи папируса Райнда соответствует значение П = 4(8/9) = 3,1605. Однако каким образом египтяне получили саму формулу, из контекста неясно.

Слайд 9

Архимед, возможно, первым предложил математический способ вычисления π. Для этого он

вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку

Слайд 10

Удваивая число правильно выписанных и удвоенных многоугольников можно получать всё более

и более точное значение числа П

Слайд 11

Индийцы и арабы полагали, что П = √10. Это значение приводит

индийский математик 7 века нашей эры Брахмагупта. Китайские учёные в 3 веке использовали для значения П 3 7/50, которое хуже приближения Архимеда. В конце 5 века Цзу Чун Чжи получил приближение 355/113 (П = 3,1415927). Оно осталось неизвестно европейцам и было вновь найдено нидерландским математиком Андрианом Антонисом лишь в 1585 году.

Слайд 12

К концу 16 века в европейской математике сформировалось понятие иррациональных и

рациональных чисел. Хотя многие были убеждены, что П иррациональное число доказать этого никто не мог. В то же время некоторые математики продолжали заниматься вычислением числа П. Нидерландский учёный Лудольф Ван Цейлен в 1615 году нашёл для него 32 правильных десятичных знака, это приближение называли лудольфовым числом.

Слайд 13

Дальнейшая история числа П напоминает спортивные соревнования, когда то один, то

другой спортсмен вырывается вперёд.

Слайд 14

Лондонский математик Джон Мэчин в 1706 году пришёл к формуле :

П/4 = 4(1/5 – 1/3∙5 + 1/5∙5 - …) – (1/239 – 1/3∙239 + 1/5∙239 - …),
которая до сих пор считается одной из лучших для приближённого вычисления П.
В 1766 году немецкий математик Иоганн Ламберт строго доказал иррациональность числа П: число П но может быть представлено простыми дробями, как бы ни были велики числитель и знаменатель.
В конце 19 века профессор Мюнхенского университета Карл Фердинанд Линдеман доказал, что П – число трансцендентное, т.е. оно не является корнем никакого алгебраического уравнения.

Слайд 15

Тайна числа П
В процессе вычислений знаков числа П было открыто множество

разных научных методов и целых наук. Но самое главное – в десятичной части числа пи нет повторений, как в обычной периодической дроби, а число знаков после запятой у него – бесконечно. На сегодняшний день проверено, что в 500 млрд. знаков числа пи повторений действительно нет. Есть основания полагать, что их нет вообще.

Слайд 16

Поскольку в последовательности знаков числа пи нет повторений – это значит,

что последовательность знаков пи подчиняется теории хаоса, точнее, число пи – это и есть хаос, записанный цифрами. Более того, при желании, можно этот хаос представить графически, и есть предположение, что этот Хаос разумен.

Слайд 17

В 1965-м году американский математик М. Улэм, сидя на одном скучном

собрании, от нечего делать начал писать на клетчатой бумаге цифры, входящие в число пи. Поставив в центре 3 и двигаясь по спирали против часовой стрелки, он выписывал 1, 4, 1, 5, 9, 2, 6, 5 и прочие цифры после запятой. Попутно он обводил все простые числа кружками. Каково же было его удивление и ужас, когда кружки стали выстраиваться вдоль прямых! Позже он сгенерировал на основе этого рисунка цветовую картину с помощью специального алгоритма. Что изображено на этой картине – засекречено.

Слайд 18