Слайд 19

Приклади.
1.Користуючись поліномною формулою, обчислити (x + y + z)3.
x3 + y3
+ z3 + 3x2y + 3x2z + 3xy2 + 3y2z + 3xz2 + 3yz2 + 6xyz. *
2. Знайти коефіцієнт при x8 у розкладанні полінома (1 + x2 – x3)9.
* Довільний член розкладання полінома має вигляд
* C9(k1, k2, k3)1k1(x2)k2(–x3)k3 = C9(k1, k2, k3)(–1)k3x2k2+3k3,
де k1, k2, k3 – невід'ємні цілі числа, а k1 + k2 + k3 = 9.
Потрібно знайти ті з них, для яких виконується 2k2 + 3k3 = 8.
Ці умови задовольняють тільки дві трійки чисел: k1 = 5, k2 = 4, k3 = 0 і
k1 = 6, k2 = 1, k3 = 2. Отже, шуканий коефіцієнт
C9(5, 4, 0)(–1)0+ C9(6, 1, 2)(–1)2 = C9(5, 4, 0) + C9(6, 1, 2) = 378. *


































 Программно-аппаратный комплекс для автоматизации управленческой деятельности школы
Программно-аппаратный комплекс для автоматизации управленческой деятельности школы Самый умный
Самый умный В мире песочных форм и фигур
В мире песочных форм и фигур Аттестационная работа. Рецензия на проектно-исследовательскую работу «Виртуальные и реальные маршруты Казани»
Аттестационная работа. Рецензия на проектно-исследовательскую работу «Виртуальные и реальные маршруты Казани» Единицы измерения площадей
Единицы измерения площадей Геометрические тела
Геометрические тела Тренажёр. Полёт бабочки. (1 класс)
Тренажёр. Полёт бабочки. (1 класс) Самый умный. Математическая игра
Самый умный. Математическая игра Преобразование выражений содержащих квадратные корни
Преобразование выражений содержащих квадратные корни Графические методы в С5
Графические методы в С5 «Ох уж эта математика» Урок в 5 классе
«Ох уж эта математика» Урок в 5 классе  Правильные многогранники. (11 класс)
Правильные многогранники. (11 класс) Множества. Комбинаторика
Множества. Комбинаторика Столбчатые диаграммы
Столбчатые диаграммы Весёлая математика. (ДОУ)
Весёлая математика. (ДОУ) Презентация по математике "Окружность" - скачать бесплатно
Презентация по математике "Окружность" - скачать бесплатно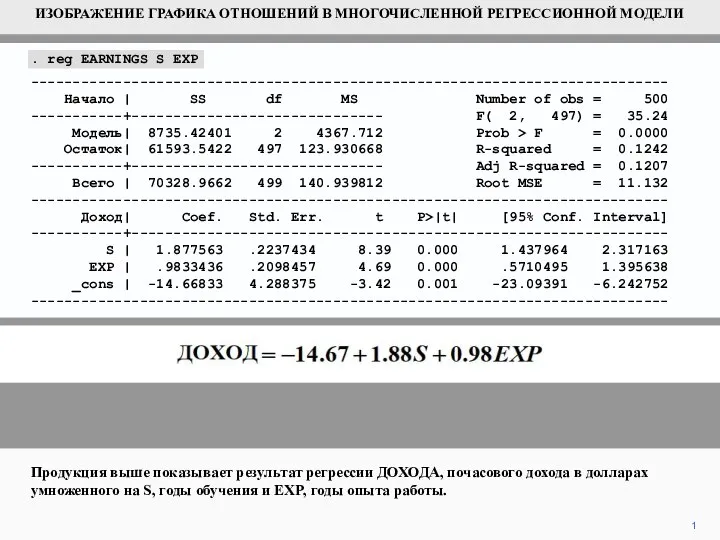 Изображение графика отношений в многочисленной регрессионной модели
Изображение графика отношений в многочисленной регрессионной модели Показникові нерівності
Показникові нерівності Касательная к окружности
Касательная к окружности Решение задач с помощью уравнений (5 класс)
Решение задач с помощью уравнений (5 класс) Устный счет
Устный счет Тема: «КОНУС»
Тема: «КОНУС» Урок математики 1 класс
Урок математики 1 класс Эйлеровы графы. Пути и циклы Эйлера
Эйлеровы графы. Пути и циклы Эйлера Презентация по математике "Преобразование двойных радикалов" - скачать
Презентация по математике "Преобразование двойных радикалов" - скачать  Теорема Пифагора
Теорема Пифагора Площадь треугольника и подобие
Площадь треугольника и подобие Тригонометрические уравнения
Тригонометрические уравнения