Содержание
- 2. Докажем, что семейство {Tξ}ξ∈V операторов Дункла является коммутативным относительно композиции. Теорема 4. Для произвольных ненулевых векторов
- 3. которую перепишем в следующем виде:
- 4. Очевидно ∂ξ∂η − ∂η∂ξ = 0. Далее, преобразуем выражение
- 5. Из эквивариантности оператора ∇ вытекает, что Поэтому рассматриваемая разность может быть преобразована к выражению
- 6. которое симметрично относительно векторов ξ и η. Но это означает, что к такому же выражению может
- 7. Преобразуем правую часть последнего равенства:
- 9. где
- 11. Рассмотрим сумму Ω1, которую преобразуем, пользуясь инвариантностью скалярного произведения относительно действия группы Коксетера. Получаем
- 12. Ясно, что при фиксированном β найдется единственный положительный корень α ′, такой что sβα = ±α
- 14. Заменяя α ′ на α, окончательно получаем, что Аналогичные рассуждения показывают, что
- 15. Меняя в последней сумме α на β и β на α, получаем Ω1 = Ω2. Покажем,
- 16. По тем же причинам, что и выше вместо sαβ можно писать β ′ и считать, что
- 17. Но внутренняя сумма в Ω3 равна нулю в силу леммы 2.1, где форма Итак, для произвольных
- 19. Скачать презентацию


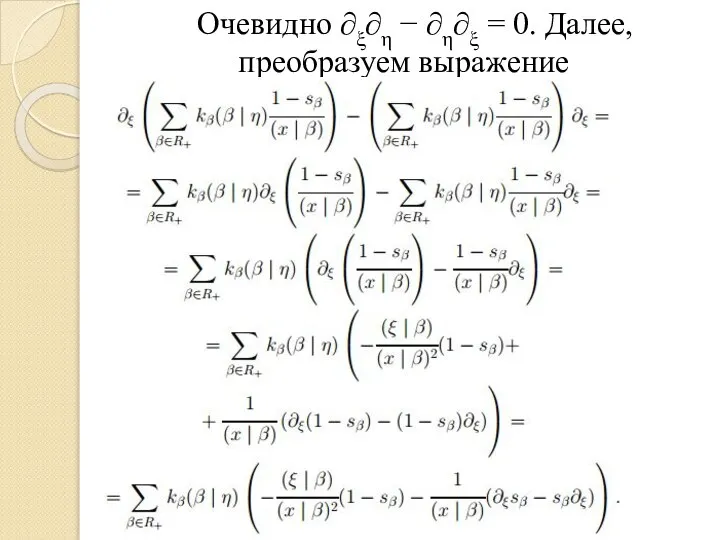



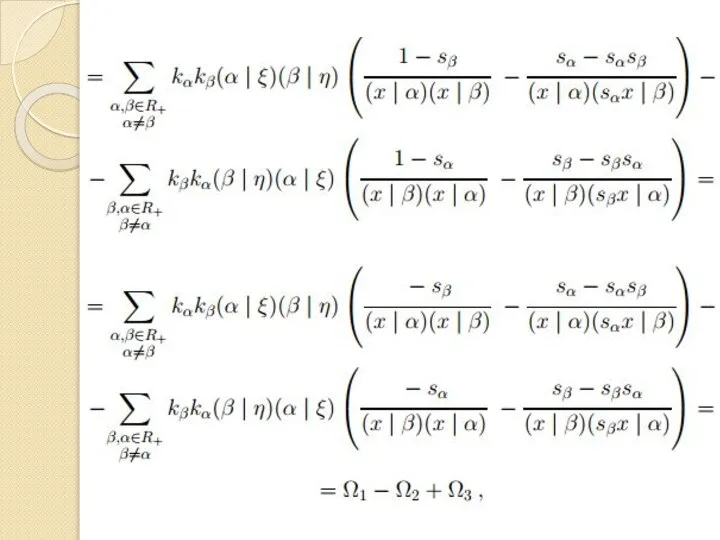

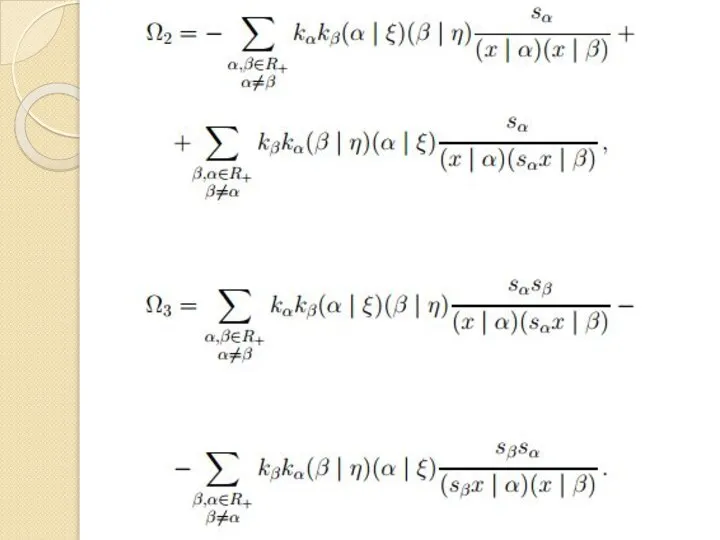







 Задача о напитках
Задача о напитках Система использования ключевых задач геометрии при обучении математике
Система использования ключевых задач геометрии при обучении математике Математика. Задания на лето. Часть 6
Математика. Задания на лето. Часть 6 Задание на исследование функции с помощью производной. ЕГЭ. Задание В14
Задание на исследование функции с помощью производной. ЕГЭ. Задание В14 Презентация на тему Состав числа 5
Презентация на тему Состав числа 5 Эконометрика
Эконометрика Множества
Множества Метод параллельного проектирования
Метод параллельного проектирования Количественный счет предметов
Количественный счет предметов Математический диктант. сложение и вычитание трёхзначных чисел
Математический диктант. сложение и вычитание трёхзначных чисел Применение теории графов к решению задач
Применение теории графов к решению задач Уравнения и неравенства. 11 класс
Уравнения и неравенства. 11 класс Задания по математике. Звездные войны
Задания по математике. Звездные войны Итоговое повторение. 9 класс (2)
Итоговое повторение. 9 класс (2) Общие сведения о формальных и аксиоматических системах
Общие сведения о формальных и аксиоматических системах Числовые функции. 10 класс
Числовые функции. 10 класс Двусвязность. (Лекция 7)
Двусвязность. (Лекция 7) Первообразная. ЕГЭ, задание В9
Первообразная. ЕГЭ, задание В9 Группировка материала статистических наблюдений
Группировка материала статистических наблюдений 6 + 7 + 6 + 8 = 7 + 7 + 7 + 7 + 7 = 9 + 9 + 9 = 3 + 4 + 5 + 3 + 4 = Чем похожи и чем отличаются эти выражения?
6 + 7 + 6 + 8 = 7 + 7 + 7 + 7 + 7 = 9 + 9 + 9 = 3 + 4 + 5 + 3 + 4 = Чем похожи и чем отличаются эти выражения?  Решение квадратных уравнений. 8 класс
Решение квадратных уравнений. 8 класс Математика ОГЭ 37 или 38
Математика ОГЭ 37 или 38 Равенство фигур. Сравнение отрезков и углов. Биссектриса угла. (7 класс)
Равенство фигур. Сравнение отрезков и углов. Биссектриса угла. (7 класс) Метрическая система мер
Метрическая система мер «Сложение и вычитание смешанных дробей»
«Сложение и вычитание смешанных дробей» Теорема Виета Франсуа Виет (1540–1603) родился во Франции. Разработал почти всю элементарную алгебру; ввёл в алгебру буквенные обо
Теорема Виета Франсуа Виет (1540–1603) родился во Франции. Разработал почти всю элементарную алгебру; ввёл в алгебру буквенные обо Алгебра и начала анализа. Профильное обучение 10 класс
Алгебра и начала анализа. Профильное обучение 10 класс Диагностическая работа по математике 9 класс в форме ОГЭ
Диагностическая работа по математике 9 класс в форме ОГЭ