Содержание
- 2. Пусть |R| = N — число корней в системе R, CN — комплексное пространство, ассоциированное с
- 3. соответственно, где γ, δ ∈ R, w ∈ W(R).
- 4. Случай A Пусть дана система корней типа An−1 (n ≥ 2). Векторное пространство V — это
- 5. где (ei) — стандартный базис в Rn . В качестве базиса можно выбрать корни αk,k+1, где
- 6. Для краткости, отражение относительно αij обозначим через sij . Таким образом, отражение однозначно определяется неупорядоченной парой
- 7. Далее, пусть даны отражения sij и skl. Когда все индексы по- парно различны, FAn−1 (αij, αkl)
- 8. Рассмотрим, например, произведение отражений sij и sik. Можно считать, что j sαsβ = ssαβsα вытекают следующие
- 9. Произведение sijsik отображает вектор (. . ., xi , . . ., xj , . .
- 10. Таким образом, уравнения, определяющие многообразие Бете-Дункла имеют вид:
- 11. Поскольку в системе типа An−1 все корни имеют одинаковую длину, то значение функции kα на всех
- 12. получаем эквивалентную систему линейных уравнений: uij − uik + ujk = uji − uki + ukj
- 13. Доказательство. В системе корней An−1 введем отношение порядка следующим образом. Пусть i l, то αij ≺
- 14. Далее, все уравнения системы (1), не входящие в указанную подсистему, являются линейными комбинациями уравнений подсистемы. В
- 15. Так как число таких уравнений равно а переменных n(n − 1), то размерность многообразия Бете-Дункла равна
- 16. в пространстве Cn(n−1) с исключенными гиперплоскостями uij − uji = 0, где 1 ≤ i Пример.
- 17. w123 = s12s13 = s23s12 = s13s23, w124 = s12s14 = s24s12 = s14s24, w134 =
- 18. Последнее уравнение этой системы, как легко видеть, является линейной комбинацией первых трех. Относительно порядка, введенного при
- 19. Поэтому система, составленная из них, линейно независима. Следовательно размерность многообразия равна 9, что согласуется с доказанной
- 20. Случай D Рассмотрим систему корней типа Dn (n ≥ 3). Относительно базиса αk−1,k = ek−1−ek (1
- 21. Отражение относительно вектора αij обозначим, как и выше, через sij , а относительно вектора βij —
- 22. Как и в предыдущем случае, произведения sijsik, sjksij , siksjk и только они, отображают вектор (.
- 23. sijσik(. . ., xi , . . ., xj , . . ., xk, . .
- 24. Координаты, отвечающие корням αij , −αij , βij , −βij , обозначим через uij, uji, vij,
- 25. После соответствующих преобразований, уравнение, отвечающее элементу sijsik, примет вид: uij − uik + ujk = uji
- 26. Для произведения sijσki уравнения имеют аналогичную форму: uij − vki + vjk = uji − vik
- 27. Напомним, что рассматриваются только положительные корни, поэтому первый индекс отражения всегда выбирается меньше второго. Таким образом,
- 28. Лемма 18. Система линейных уравнений (3) эквивалентна системе (2) и линейно независима.
- 29. Доказательство. Линейная независимость уравнений системы устанавливается по ее матрице, которая при подходящем выборе по- рядка во
- 30. ui,i+3 − vi,i+1 + vi+1,i+3 = ui+3,i − vi+1,i + vi+3,i+1 из ui,i+3 − vi,i+2 +
- 31. Точно также разность уравнений ui,i+1 − vij + vi+1,j = ui+1,i − vji + vj,i+1 и
- 32. Таким образом, каждое уравнение системы (3) является линейной комбинацией уравнений системы (2). Далее, уравнение uij −
- 33. Каждое из последних уравнений можно получить из уравнений системы (3). Например, уравнение uij − vi,j+2 +
- 35. Аналогичные рассуждения проходят и для остальных уравнений системы, что завершает доказательство леммы. (доказано) Доказанная лемма позволяет
- 37. Скачать презентацию


































 Теорема о вписанном угле
Теорема о вписанном угле МАТЕМАТИКА 5 кл. История натуральных чисел. Пестрова Елена Алексеевна, МБОУ Сош. № 1 Ст. Полтавская. Исто
МАТЕМАТИКА 5 кл. История натуральных чисел. Пестрова Елена Алексеевна, МБОУ Сош. № 1 Ст. Полтавская. Исто Урок математики по теме: «Единицы времени»
Урок математики по теме: «Единицы времени» Презентация по математике "Решение планиметрических задач на нахождение площади фигуры" - скачать бесплатно
Презентация по математике "Решение планиметрических задач на нахождение площади фигуры" - скачать бесплатно Геометрический смысл производной
Геометрический смысл производной Движение. Его виды и применение. 9 класс
Движение. Его виды и применение. 9 класс Найрозумніший математик. Викторина
Найрозумніший математик. Викторина Параллелепипед. Куб
Параллелепипед. Куб Презентация на тему Теорема Виета
Презентация на тему Теорема Виета 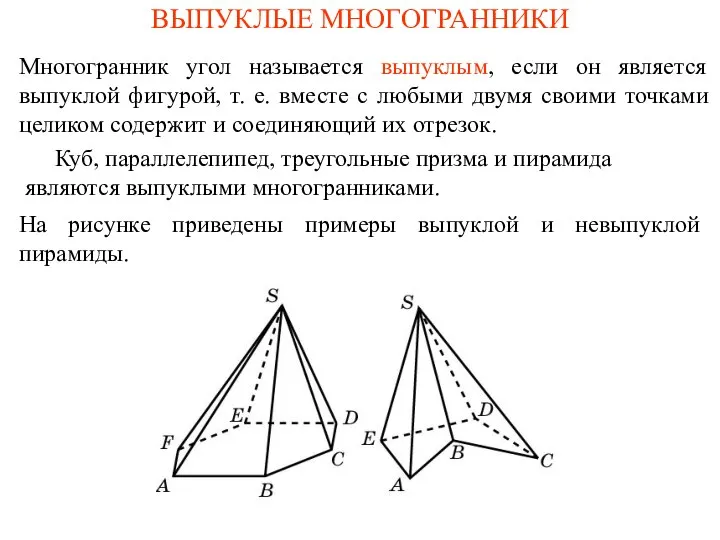 Выпуклые многогранники
Выпуклые многогранники Методы мотивации и стимулирования деятельности обучающихся на уроках математики
Методы мотивации и стимулирования деятельности обучающихся на уроках математики Ранг матрицы
Ранг матрицы Построение сечений призмы
Построение сечений призмы Вычисление значений числовых выражений с действиями разной степени
Вычисление значений числовых выражений с действиями разной степени Игра по математике для 6 класса «Счастливый случай»
Игра по математике для 6 класса «Счастливый случай» Делимость чисел Выполнил: Нещеретнев Андрей, ученик 7 «А» класса. Руководитель:
Делимость чисел Выполнил: Нещеретнев Андрей, ученик 7 «А» класса. Руководитель:  Треугольники
Треугольники Arctg, arcctg. Решение уравнений tgt=a, ctgt=a
Arctg, arcctg. Решение уравнений tgt=a, ctgt=a 2 класс МБОУ « СОШ № 2 г. Рузы»
2 класс МБОУ « СОШ № 2 г. Рузы»  Игра "Счастливый случай". Внеклассное мероприятие по математике
Игра "Счастливый случай". Внеклассное мероприятие по математике ВОЗНИКНОВЕНИЕ ИЗМЕРЕНИЙ В ДРЕВНОСТИ Выполнил кадет 5А взвода МОУ «КСОШ № 2» Вольных Евгений
ВОЗНИКНОВЕНИЕ ИЗМЕРЕНИЙ В ДРЕВНОСТИ Выполнил кадет 5А взвода МОУ «КСОШ № 2» Вольных Евгений  Кривые второго порядка. Эллипс, гипербола, парабола
Кривые второго порядка. Эллипс, гипербола, парабола Какие бывают графы
Какие бывают графы Непараметрические критерии
Непараметрические критерии Умножение и деление на 10
Умножение и деление на 10 Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Равновеликие и равносоставленные фигуры. Метапредмет – хаос и порядок
Равновеликие и равносоставленные фигуры. Метапредмет – хаос и порядок Общие вопросы измерений
Общие вопросы измерений