Содержание
- 2. Комплексные числа 1.Историческая открытия. 2. Основные понятия. а) Геометрическое изображение комплексных чисел б) Модуль и аргумент
- 3. 1. Историческая справка Впервые мнимые величины появились в работе Дж. Кардано «Великое искусство, или об алгебраических
- 4. Абрамах Муавр (Moivre) (1667 – 1754) Абрахам Муавр – английский математик. Муавр нашел (1707) правила возведения
- 5. Карл Фридрих Гаусс (Gauss) (1777 – 1855) Карл Фридрих Гаусс – немецкий математик. Работы Гаусса оказали
- 6. Леонард Эйлер (Eular) (1707 – 17830) Леонард Эйлер - математик, академик Петербургской академии наук. В его
- 7. Основные понятия Комплексным числом называется выражение вида z=a+bi , где a и b действительные числа, а
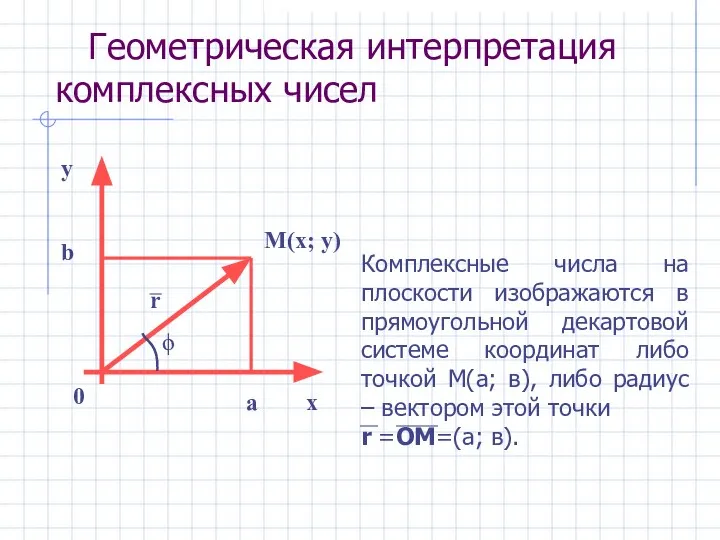
- 8. Геометрическая интерпретация комплексных чисел Комплексные числа на плоскости изображаются в прямоугольной декартовой системе координат либо точкой
- 9. Модуль и аргумент комплексного числа Модуль комплексного числа Аргумент комплексного числа Arg z =ϕ +2πn, n∈z,
- 10. Найти модуль комплексного числа Вычислить По знакам и определить четверть, в которой заканчивается искомый угол Найти
- 11. 6. Формы записи комплексных чисел Алгебраическая z =a + bi Тригонометрическая z = r (cos φ
- 12. 7. Переход от алгебраической формы комплексных чисел к тригонометрической и показательной без использования алгоритма z1 =
- 13. Переход от алгебраической формы комплексных чисел к тригонометрической и показательной с использованием алгоритма Z = 2
- 14. Практическое применение
- 15. Комплексные числа в экономике Сегодня сложно представить себе ряд наук без применения комплексных чисел. Теория электротехники,
- 16. Товар является носителем двух составляющих: потребительских свойств, объективно присущих товару, и цены - денежной оценки потребительских
- 18. Скачать презентацию














 Окружность. Обобщающий урок в 8 классе по геометрии к дню космонавтики
Окружность. Обобщающий урок в 8 классе по геометрии к дню космонавтики Треугольники. Подготовка к ОГЭ. Задание 16
Треугольники. Подготовка к ОГЭ. Задание 16 Задачи на проценты. 5 класс
Задачи на проценты. 5 класс Применение распределительного свойства умножения
Применение распределительного свойства умножения Симметрия
Симметрия ГОУ Центр Образования № 2006 «Деление круглых чисел».
ГОУ Центр Образования № 2006 «Деление круглых чисел».  Shortest Paths
Shortest Paths Дробно-рациональные уравнения
Дробно-рациональные уравнения Аттестационная работа. Словарь терминов по элементарной геометрии
Аттестационная работа. Словарь терминов по элементарной геометрии РАЗВИТИЕ ЛОГИЧЕСКОГО МЫШЛЕНИЯ-2
РАЗВИТИЕ ЛОГИЧЕСКОГО МЫШЛЕНИЯ-2  Элементы теории вероятностей и статистики. Решение задач на доверительные интервалы
Элементы теории вероятностей и статистики. Решение задач на доверительные интервалы Координатная плоскость. Формирование межпредметных понятий на уроке математики в 6 классе
Координатная плоскость. Формирование межпредметных понятий на уроке математики в 6 классе Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Одночлен и его стандартный вид. 7 класс
Одночлен и его стандартный вид. 7 класс Случайные величины и их числовые характеристики. Законы распределения дискретных случайных величин (ДСВ)
Случайные величины и их числовые характеристики. Законы распределения дискретных случайных величин (ДСВ) Деление числа на десятичную дробь
Деление числа на десятичную дробь Расчёт корреляционных зависимостей в Excel
Расчёт корреляционных зависимостей в Excel Этот вездесущий треугольник
Этот вездесущий треугольник Тестовый контроль знаний, как основа диагностики качества обучения
Тестовый контроль знаний, как основа диагностики качества обучения Новые мерки и умножение урок 22, с. 64-66 учебник Петерсон Л.Г.
Новые мерки и умножение урок 22, с. 64-66 учебник Петерсон Л.Г. Спектральное представление ССП
Спектральное представление ССП Нелинейные системы автоматического управления
Нелинейные системы автоматического управления Числа от 1 до 20. Решение задач и выражений
Числа от 1 до 20. Решение задач и выражений Килограмм математика 1 класс Подготовила Ануфриева Е.В. учитель начальных классов
Килограмм математика 1 класс Подготовила Ануфриева Е.В. учитель начальных классов  ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности  Анализ системы упражнений учебника и построение комплекса заданий для работы с одаренными учащимися
Анализ системы упражнений учебника и построение комплекса заданий для работы с одаренными учащимися Системы счисления
Системы счисления Презентация по математике "Симметрия" - скачать
Презентация по математике "Симметрия" - скачать