Содержание
- 2. Лекция 4 2. Многочлены в комплексной области. 1. Комплексная функция действительного аргумента. Комплексные функции и многочлены.
- 4. В алгебраической форме z(t) выглядит так:
- 5. Отсюда, в частности, следует правило дифференцирования комплексной функции:
- 6. Пример: Решение. действительно,
- 7. Рассмотрим многочлен порядка n: Здесь z - комплексная переменная.
- 9. Как и в элементарной алгебре справедливо основное свойство деления: Здесь:
- 10. Корни многочлена ( деление без остатка)
- 11. В развернутом виде: Такое уравнение называется алгебраическим уравнением n-ой степени. Теорема Безу.
- 12. Доказательство. По условию: По основному свойству деления: Пложим z = a, тогда
- 13. Следствие. и т.д.
- 15. Основная теорема алгебры Многочлен n-ой степени имеет ровно n корней, если каждый корень считать столько раз,
- 16. Таким образом: Комплексные корни многочлена с действительными коэффициентами являются сопряженными парами корней .
- 17. Из теоремы Безу и основной теоремы алгебры следует, что всякий многочлен степени n можно разложить на
- 18. Здесь …………………………..
- 19. 1. Линейные множители - соответствуют действительным корням zi кратности ki, 2. Квадратичные множители где p,q -
- 20. Для доказательства последнего рассмотрим: Здесь:
- 21. Таким образом, многочлен с действительными коэффициентами имеет разложение:
- 22. Пример: Решение. Действительных корней нет. Комплексные корни:
- 26. Скачать презентацию


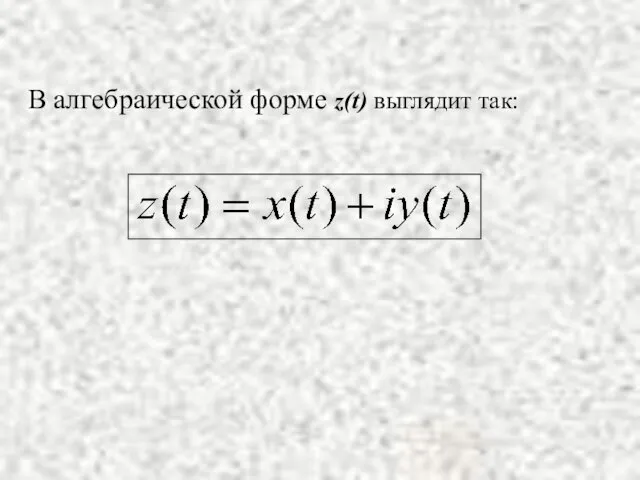



















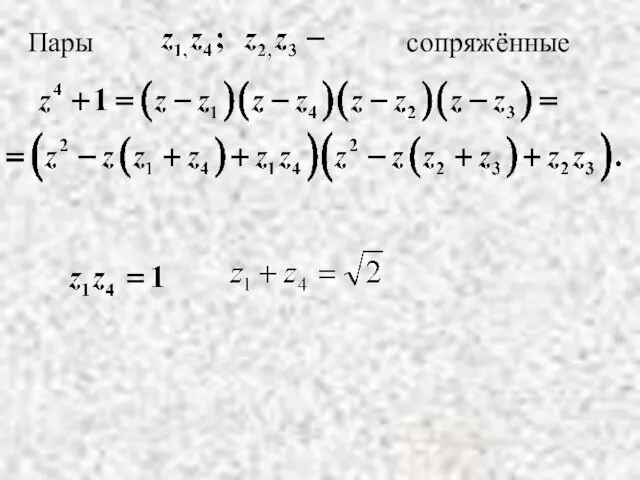
 Странички для любознательных. Что узнали. Чему научились. 2 класс
Странички для любознательных. Что узнали. Чему научились. 2 класс Общая постановка задачи оптимизации
Общая постановка задачи оптимизации Математика
Математика Презентация по математике "Вычисление площадей с помощью интегралов" - скачать
Презентация по математике "Вычисление площадей с помощью интегралов" - скачать  Урок геометрии в 7 классе
Урок геометрии в 7 классе Примеры, уравнения, дроби с дополнительным множителем
Примеры, уравнения, дроби с дополнительным множителем НОК – наименьшее общее кратное. 6 класс
НОК – наименьшее общее кратное. 6 класс Круги, окружности и шары вокруг нас. 6 класс
Круги, окружности и шары вокруг нас. 6 класс Дифференциальное исчисление функций одной переменной
Дифференциальное исчисление функций одной переменной Творческая работа НА ТЕМУ: ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
Творческая работа НА ТЕМУ: ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ Система технических измерений
Система технических измерений Площадь многоугольников
Площадь многоугольников Физико-математическая викторина В бесконечность…
Физико-математическая викторина В бесконечность… Геометрия. Конус
Геометрия. Конус Объём и поверхность тел вращения. Вычисление комфортности жилища
Объём и поверхность тел вращения. Вычисление комфортности жилища Дискретная случайная величина
Дискретная случайная величина Действие умножение. Знак умножения
Действие умножение. Знак умножения Числовые функции 9 класс В реальной жизни мы говорим: «каковы мои функции» или
Числовые функции 9 класс В реальной жизни мы говорим: «каковы мои функции» или  Тренажёр В гости к Матроскину. Математика
Тренажёр В гости к Матроскину. Математика Готовимся к ГИА. Элементарные функции
Готовимся к ГИА. Элементарные функции Из чего строится геометрия? Заббарова Ландыш Вазыховна Ново-Савиновский район Гимназия №13 Геометрия 7-8 класс.
Из чего строится геометрия? Заббарова Ландыш Вазыховна Ново-Савиновский район Гимназия №13 Геометрия 7-8 класс. Тест по теме: "Пирамида". Часть 1
Тест по теме: "Пирамида". Часть 1 Определители и их свойства. Лекции 9,10
Определители и их свойства. Лекции 9,10 Презентация на тему Повторение и закрепление знаний по теме «Тригонометрические формулы»
Презентация на тему Повторение и закрепление знаний по теме «Тригонометрические формулы» Обобщение понятия о показателе степени
Обобщение понятия о показателе степени Геометрическая прогрессия Повторение
Геометрическая прогрессия Повторение Презентация по математике "Логические задачи на переправу без чисел" - скачать
Презентация по математике "Логические задачи на переправу без чисел" - скачать  Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел