Содержание
- 2. Совершенная нормальная форма Среди множества эквивалентных формул, представляющих выбранную булеву функцию f, выделяется одна формула, которая
- 3. Обозначения x,σ∈B={0,1}
- 4. Теорема о дизъюнктивном разложении функции f(x1,…,xn) по k переменным Любую булеву функцию f(x1,x2,…,xn) можно представить в
- 5. Теорема о дизъюнктивном разложении функции Запись означает многократную дизъюнкцию, которая берется по всем возможным наборам значений
- 6. Пример Получить дизъюнктивное разложение функции по переменным x, z. Подставим f(0,y,0,t), f(0,y,1,t), f(1,y,0,t), f(1,y,1,t) в формулу
- 7. Дизъюнктивное разложение булевой функции f(x1,x2,…,xn) по одной переменной Любую булеву функцию f(x1,x2,…,xn) можно представить в следующей
- 8. Дизъюнктивное разложение булевой функции f(x1,x2,…,xn) по всем n переменным Любую булеву функцию f(x1,x2,…,xn)≠0 можно представить в
- 9. Пример Получить дизъюнктивное разложение функции по всем переменным. Определим значение функции на каждой из интерпретаций:
- 10. Определения и понятия Элементарной конъюнкцией называется конъюнкция любого числа булевых переменных, взятых с отрицанием или без
- 11. Определения и понятия Дизъюнктивной нормальной формой (ДНФ) называется формула, представленная в виде дизъюнкции элементарных конъюнкций. Примеры:
- 12. Определения и понятия Элементарная конъюнкция x1σ1∧x2σ2∧… ∧xnσn называется конституентой единицы (минтермом) функции f(x1,x2,…,xn), если f(σ1,σ2,…,σn)=1, то
- 13. Свойства конституенты единицы Конституента единицы функции n переменных имеет вид x1σ1∧x2σ2∧…∧xnσn и соответствует интерпретации (σ1,σ2,…,σn). Конституента
- 14. Определение и понятия Совершенной дизъюнктивной нормальной формой (СДНФ) булевой функции называется формула, представленная в виде дизъюнкции
- 15. Определения и понятия Совершенной конъюнктивной нормальной формой (СКНФ) функции называется формула, представленная в виде конъюнкции конституент
- 16. Следствия из определений СДНФ и СКНФ булевых функций Для каждой булевой функции f(x1,x2,…,xn), не являющейся константой
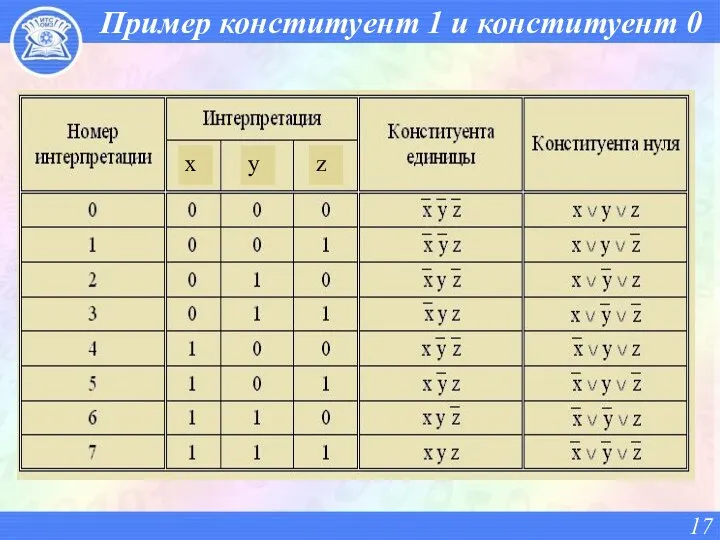
- 17. Пример конституент 1 и конституент 0 x y z
- 18. Алгоритм перехода от таблицы истинности булевой функции к СДНФ Выделить все интерпретации (σ1,σ2,…,σn), на которых значение
- 19. Алгоритм перехода от таблицы истинности булевой функции к СДНФ. Пример Получить СДНФ для функций f13(x,y). Функция
- 20. Алгоритм перехода от таблицы истинности булевой функции к СКНФ Выделить все интерпретации (σ1,σ2,…,σn), на которых значение
- 21. Алгоритм перехода от таблицы истинности булевой функции к СКНФ Пример Получить СКНФ для функций f7(x,y) и
- 22. Алгоритм построения таблицы истинности функции, заданной СДНФ Построить таблицу истинности, содержащую 2n интерпретаций вида (σ1,σ2,…,σn). Отметить
- 23. Алгоритм перехода от произвольной формулы алгебры логики к СДНФ Исключить константы, используя законы действий с константами.
- 24. Алгоритм перехода от произвольной формулы алгебры логики к СДНФ. Продолжение Построить конституенты единицы функции, введением в
- 26. Скачать презентацию






















 МОУ «Лицей №17» Фестиваль «Портфолио» Автор: Шульгина Дарья ученица 7
МОУ «Лицей №17» Фестиваль «Портфолио» Автор: Шульгина Дарья ученица 7  Математические фокусы - мистические способности или алгоритм
Математические фокусы - мистические способности или алгоритм Презентация по математике "Сложение и вычитание двузначныз чисел" - скачать бесплатно
Презентация по математике "Сложение и вычитание двузначныз чисел" - скачать бесплатно Исследование математических фокусов
Исследование математических фокусов Координатная плоскость
Координатная плоскость Решение показательных уравнений и неравенств
Решение показательных уравнений и неравенств Дискриминантный анализ
Дискриминантный анализ Сложение и вычитание многочленов. 7 класс
Сложение и вычитание многочленов. 7 класс Слайд-лекции по дисциплине Высшая математика
Слайд-лекции по дисциплине Высшая математика Линейная алгебра
Линейная алгебра Построение графиков функции разного вида в программе EXEL
Построение графиков функции разного вида в программе EXEL Движение плоскости. (9 класс)
Движение плоскости. (9 класс) Старинные системы мер
Старинные системы мер Признаки и свойства параллельных прямых
Признаки и свойства параллельных прямых Невозможные фигуры
Невозможные фигуры Проектирование последовательностных схем
Проектирование последовательностных схем Презентация на тему Делители и кратные
Презентация на тему Делители и кратные  Архимед. Открытия Архимеда
Архимед. Открытия Архимеда Четырёхугольники. Сказка - вопрос
Четырёхугольники. Сказка - вопрос Математические функции и их применение
Математические функции и их применение Исследовательская работа на уроках математики Учитель математики Ледовская Евгения Николаевна
Исследовательская работа на уроках математики Учитель математики Ледовская Евгения Николаевна Геометрические определения
Геометрические определения Тема «Функция. Свойства функций» Архипова Ирина Викторовна, МОУ СОШ №4 г.Миньяр, Челябинская область
Тема «Функция. Свойства функций» Архипова Ирина Викторовна, МОУ СОШ №4 г.Миньяр, Челябинская область  Техника дифференцирования и интегрирования
Техника дифференцирования и интегрирования Вычисление площадей фигур
Вычисление площадей фигур Упрощение выражений (5 класс)
Упрощение выражений (5 класс) Брейн-ринг. Геометрия
Брейн-ринг. Геометрия Аттестационная работа. Значение включения в программу занятий со школьниками материала, освоенного в рамках курсов
Аттестационная работа. Значение включения в программу занятий со школьниками материала, освоенного в рамках курсов