Содержание
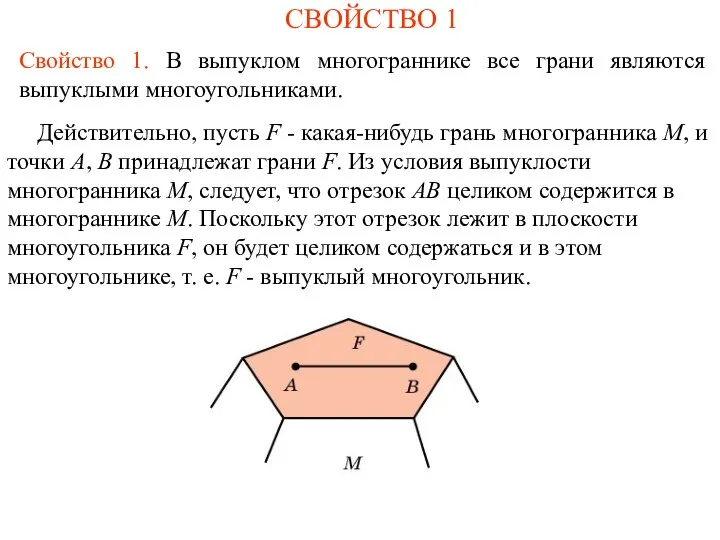
- 2. СВОЙСТВО 1 Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками. Действительно, пусть F -
- 3. СВОЙСТВО 2 Действительно, пусть M - выпуклый многогранник. Возьмем какую-нибудь внутреннюю точку S многогранника M, т.
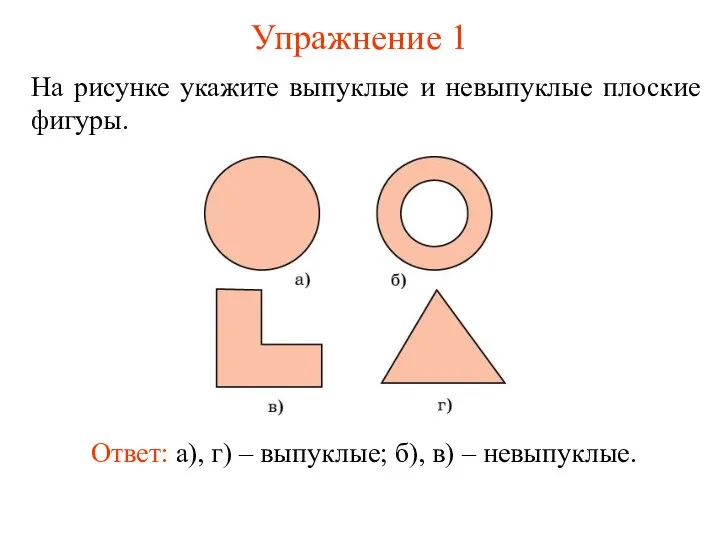
- 4. Упражнение 1 На рисунке укажите выпуклые и невыпуклые плоские фигуры. Ответ: а), г) – выпуклые; б),
- 5. Упражнение 2 Всегда ли пересечение выпуклых фигур является выпуклой фигурой? Ответ: Да.
- 6. Упражнение 3 Всегда ли объединение выпуклых фигур является выпуклой фигурой? Ответ: Нет.
- 7. Упражнение 4 Можно ли составить выпуклый четырёхгранный угол с такими плоскими углами: а) 56о, 98о, 139о
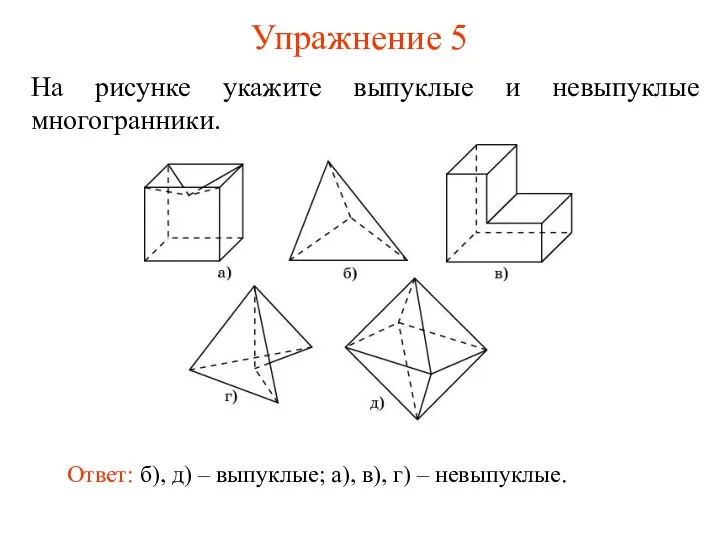
- 8. Упражнение 5 На рисунке укажите выпуклые и невыпуклые многогранники. Ответ: б), д) – выпуклые; а), в),
- 9. Упражнение 6 Может ли невыпуклый многоугольник быть гранью выпуклого многогранника? Ответ: Нет.
- 10. Упражнение 7 Может ли сечением выпуклого многогранника плоскостью быть невыпуклый многоугольник? Ответ: Нет.
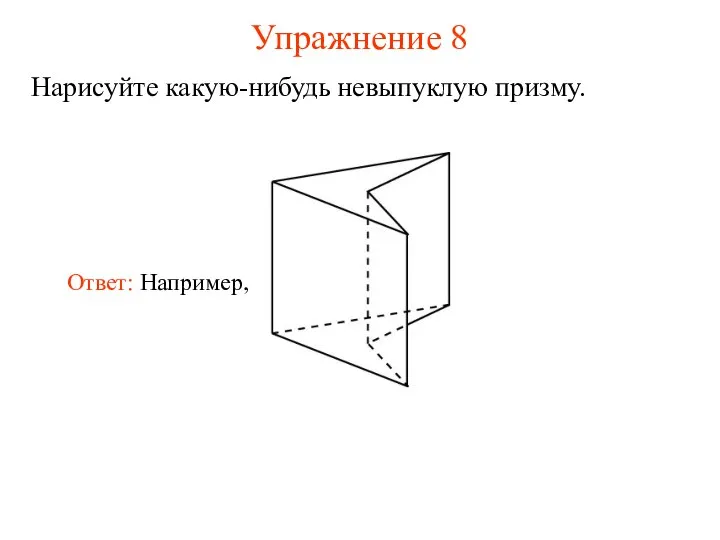
- 11. Упражнение 8 Нарисуйте какую-нибудь невыпуклую призму.
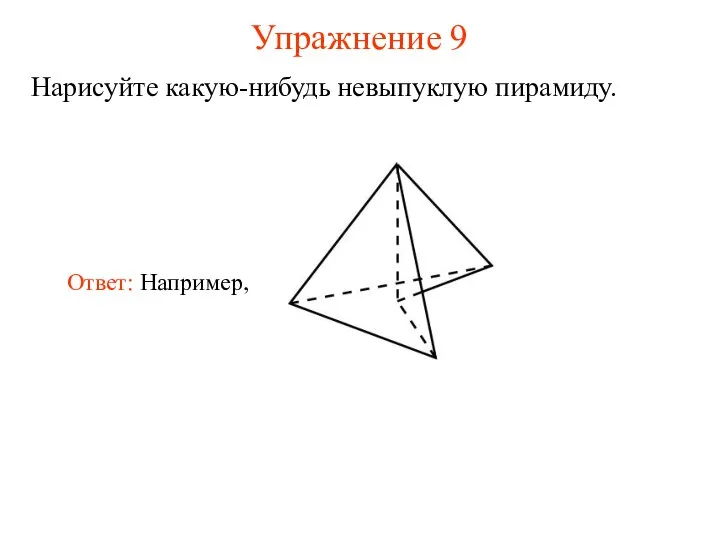
- 12. Упражнение 9 Нарисуйте какую-нибудь невыпуклую пирамиду.
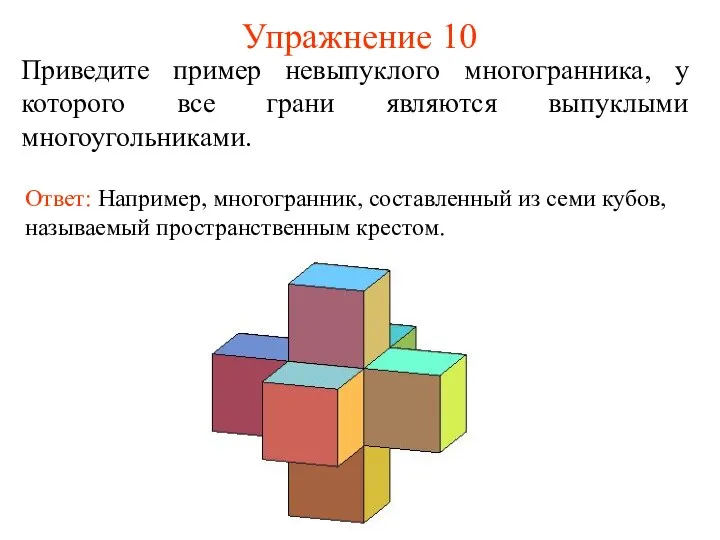
- 13. Упражнение 10 Приведите пример невыпуклого многогранника, у которого все грани являются выпуклыми многоугольниками. Ответ: Например, многогранник,
- 14. Упражнение 11* Докажите, что для любого n > 7 существует многогранник с n ребрами. Решение. Если
- 15. Упражнение 12* Докажите, что для у любого многогранника найдутся две грани с одинаковым числом ребер. Приведите
- 16. Упражнение 13* Докажите, что для у любого многогранника найдутся две вершины, в которых сходится одинаковое число
- 17. Упражнение 14* Докажите, что для у любого многогранника число граней с нечетным числом ребер четно. Решение.
- 19. Скачать презентацию










 Решение иррациональных уравнений и неравенств. 10 класс
Решение иррациональных уравнений и неравенств. 10 класс Нахождение дроби от числа
Нахождение дроби от числа Симметрия в пространстве. Правильные многогранники
Симметрия в пространстве. Правильные многогранники Простейшие преобразования графиков функций
Простейшие преобразования графиков функций Періодичність функцій. Властивості та графіки тригонометричних функцій. Розв’язування вправ
Періодичність функцій. Властивості та графіки тригонометричних функцій. Розв’язування вправ Округление десятичных дробей
Округление десятичных дробей Комп’ютерна математика: можливості і сфери застосування
Комп’ютерна математика: можливості і сфери застосування Сумма углов треугольника. Лаборатория экспериментов
Сумма углов треугольника. Лаборатория экспериментов Доли . Обыкновенные дроби
Доли . Обыкновенные дроби Что такое цифра
Что такое цифра Число и цифра 5. Письмо цифры 5
Число и цифра 5. Письмо цифры 5 Решение тригонометрических уравнений
Решение тригонометрических уравнений Algorytmy geometryczne
Algorytmy geometryczne Геометрическая вероятность
Геометрическая вероятность Decimals
Decimals Синус и косинус
Синус и косинус Газета математического кружка
Газета математического кружка Санау жүйелері (Екілік, сегіздік, ондық, он алтылық)
Санау жүйелері (Екілік, сегіздік, ондық, он алтылық) Комплексные числа
Комплексные числа Свойства параллельных плоскостей
Свойства параллельных плоскостей Многогранник, призма и их элементы
Многогранник, призма и их элементы Геометрический смысл производной
Геометрический смысл производной Случайные погрешности
Случайные погрешности Логические операции компьютеров
Логические операции компьютеров Интегрирование дробно-рациональной функции. Метод неопределенных коэффициентов
Интегрирование дробно-рациональной функции. Метод неопределенных коэффициентов Координаты на прямой
Координаты на прямой Десятичные дроби
Десятичные дроби Диагностическая работа (1 класс)
Диагностическая работа (1 класс)