Содержание
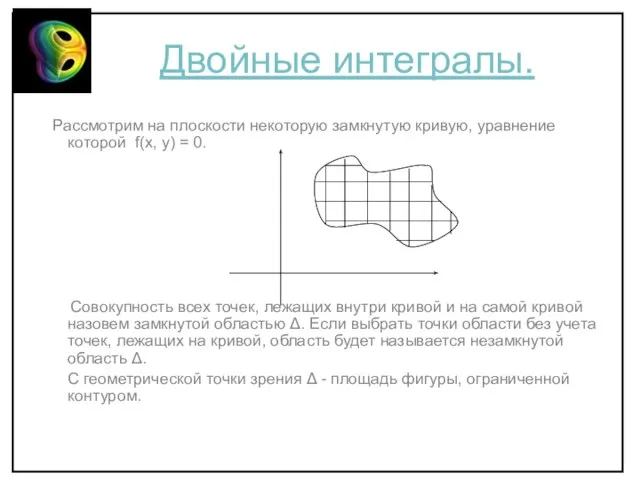
- 2. Двойные интегралы. Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой f(x, y) = 0. Совокупность всех
- 3. Разобьем область Δ на n частичных областей сеткой прямых, отстоящих друг от друга по оси х
- 4. Определение Если при стремлении к нулю шага разбиения области Δ интегральные суммы имеют конечный предел, то
- 5. Условия существования двойного интеграла Сформулируем достаточные условия существования двойного интеграла Теорема. Если функция f(x, y) непрерывна
- 6. Теорема Если функция f(x, y) ограничена в замкнутой области Δ и непрерывна в ней всюду, кроме
- 7. Свойства двойного интеграла. 1) 2) 3) Если Δ = Δ1 + Δ2, то 4) Теорема о
- 8. Вычисление двойного интеграла Теорема Если функция f(x, y) непрерывна в замкнутой области Δ, ограниченной линиями х
- 9. Теорема. Если функция f(x, y) непрерывна в замкнутой области Δ, ограниченной линиями y = c, y
- 10. Замена переменных в двойном интеграле Расмотрим двойной интеграл вида , где переменная изменяется в пределах от
- 11. т.к. при первом интегрировании переменная принимается за постоянную, то подставляя это выражение в записанное выше соотношение
- 12. Выражение называется определителем Якоби или Якобианом функций и (Якоби Карл Густав Якоб – (1804-1851) – немецкий
- 14. Скачать презентацию










 Бенефис одной задачи «Пчелиный рой» Галкина Анастасия МОУ «СОШ с.Натальин Яр Перелюбского муниципального района Саратовской о
Бенефис одной задачи «Пчелиный рой» Галкина Анастасия МОУ «СОШ с.Натальин Яр Перелюбского муниципального района Саратовской о Интегрированный урок математики с Основами православной культуры 5 класс «Микрокалькулятор» «Икона» Учитель математики п.
Интегрированный урок математики с Основами православной культуры 5 класс «Микрокалькулятор» «Икона» Учитель математики п.  Угол между прямой и плоскостью
Угол между прямой и плоскостью Измерение отрезков и углов. Учитель математики Овакимян Елена Вячеславовна ЦО № 354 им. Д.М. Карбышева
Измерение отрезков и углов. Учитель математики Овакимян Елена Вячеславовна ЦО № 354 им. Д.М. Карбышева Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Теоремы об углах, образованных двумя параллельными прямыми и секущей
Теоремы об углах, образованных двумя параллельными прямыми и секущей Алгоритм и его формальное исполнение. Типы алгоритмических структур
Алгоритм и его формальное исполнение. Типы алгоритмических структур Презентация на тему МАТЕМАТИЧЕСКИЙ ВЕЧЕР ДЛЯ СТАРШЕКЛАССНИКОВ
Презентация на тему МАТЕМАТИЧЕСКИЙ ВЕЧЕР ДЛЯ СТАРШЕКЛАССНИКОВ  Равнобедренный треугольник. (6 класс)
Равнобедренный треугольник. (6 класс) Структура курсовой работы по дисциплине «Элементарная математика»
Структура курсовой работы по дисциплине «Элементарная математика» Способы решения квадратных уравнений
Способы решения квадратных уравнений Линейное диофантово уравнение и 4 способа его решения
Линейное диофантово уравнение и 4 способа его решения ГИА - 2016. Открытый банк заданий по математике. Задача №18
ГИА - 2016. Открытый банк заданий по математике. Задача №18 Упрощение выражений
Упрощение выражений Математическая регата (8 класс)
Математическая регата (8 класс) Графическое решений квадратных уравнений
Графическое решений квадратных уравнений Цифри та числа, їх властивості та дії над ними
Цифри та числа, їх властивості та дії над ними Транспортная задача с фиксированными перевозками
Транспортная задача с фиксированными перевозками Виды показательных уравнений. 11 класс
Виды показательных уравнений. 11 класс Деление суммы на число
Деление суммы на число Геометрия вокруг нас
Геометрия вокруг нас Кластеризация значений пикселей изображений с учетом метрики цветового различия CIEDE-2000
Кластеризация значений пикселей изображений с учетом метрики цветового различия CIEDE-2000 Формулы сокращенного умножения
Формулы сокращенного умножения Методы измерения физических величин
Методы измерения физических величин Параллельный перенос
Параллельный перенос Основы математического анализа
Основы математического анализа Гаусс, Карл Фридрих
Гаусс, Карл Фридрих Язык логики высказываний
Язык логики высказываний