Лекция 13 по математике за 2 семестр

Август 4, 2022

Главная
Математика
Лекция 13 по математике за 2 семестр

Содержание

2. 3.2 Определённые интегралы 3.2.1 Основные понятия Пусть на отрезке [a;b] задана функция y=f(x). Разобьём этот отрезок
3. Свойства определённого интеграла Свойства определённого интеграла аналогичны свойствам неопределённого интеграла. Дополнительные свойства: 1. , где ;
4. 1. Использование формулы Ньютона-Лейбница. Пусть f(x) непрерывна на отрезке [a;b] и F(x) – одна из её
5. 2. Использование замены переменной. Необходимо вычислить интеграл , где f(x) –непрерывная функция на [a;b]. Перейдем к
6. 3.2 Определённые интегралы 3.2.2 Способы вычисления определённого интеграла Пример 2 Вычислить определённый интеграл . Решение. Ответ:
7. Пусть на отрезке [a;b] задана неотрицательная непрерывная функция y=f(x). Фигура, ограниченная сверху графиком y=f(x), снизу –
8. Если фигура, площадь которой необходимо вычислить, ограничена сверху графиком функции y=f(x), снизу – графиком функции y=g(x),
9. Частным случаем при этом является нахождение площади фигуры, ограниченной сверху осью Оx, снизу – графиком функции
10. В некоторых случаях, чтобы вычислить площадь искомой фигуры, необходимо разбить её на сумму или разность двух
11. Пример 3 Вычислить площадь фигуры, ограниченной графиками функций y=2x2, y=2. Решение. 1. Вершиной параболы y=2x2 является
12. 3. Используя найденные точки, строим графики заданных функций в декартовой системе координат. 4. Сверху фигура ограничена
13. Пример 4 Вычислить площадь фигуры, ограниченной кривой y=x2+x, прямыми x= –1, x=2 и осью Оx. Решение.
14. 2. Точка пересечения параболы и прямой x = –1 находится из системы: а с прямой находится
15. 3. Используя найденные точки, строим графики заданных функций в декартовой системе координат. 4. Площадь искомой фигуры
16. Если фигура, площадь которой необходимо вычислить, ограничена слева осью Oy, справа – графиком функции x=f(y), а
17. Если фигура, площадь которой необходимо вычислить, ограничена слева графиком функции x=g(y), справа – графиком функции x=f(y),
18. Пример 5 Вычислить площадь фигуры, ограниченной кривой x= –2y2–1, прямой y= –1 и осями координат. Решение.
19. 2. Точка пересечения параболы и прямой y= –1 находится из системы: с осью Оx (y=0): с
20. 3. Используя найденные точки, строим графики заданных функций в декартовой системе координат. 4. Слева фигура ограничена
21. Интегральное исчисление активно используется в экономике: степень неравенства в распределении доходов, задача дисконтирования денежного потока, вычисление
22. 3.3 Применение интегралов в экономике Пример 6 Функция предельных издержек некоторого предприятия имеет вид . Найти
23. 3.3 Применение интегралов в экономике Пример 7 Найти стоимость перевозки М т груза по железной дороге
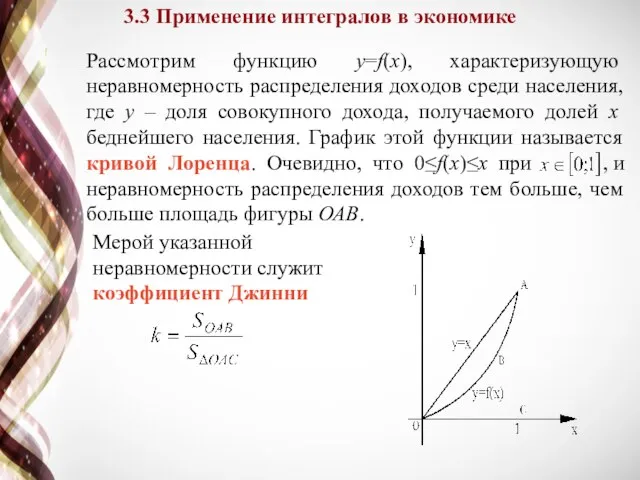
24. 3.3 Применение интегралов в экономике Рассмотрим функцию y=f(x), характеризующую неравномерность распределения доходов среди населения, где y
25. 3.3 Применение интегралов в экономике Пример 8 По данным исследований в распределении доходов одной из стран,
26. Вычислим коэффициент Джинни: это означает, что 40% наиболее низко оплачиваемого населения получает 21% совокупного национального дохода.
28. Скачать презентацию

Слайд 2

3.2 Определённые интегралы
3.2.1 Основные понятия
Пусть на отрезке [a;b] задана функция y=f(x).

Разобьём этот отрезок на n частей точками .
На каждом малом отрезке [xi–1; xi], где , выберём
точку ξi, найдём значение функции в этой точке f(ξi) и составим сумму , где .
Сумма Jn называется интегральной суммой для функции y=f(x) на [a;b].
Определённым интегралом от функции f(x) на отрезке [a;b] называется предел интегральной суммы Jn при условии, что длина наибольшего частичного отрезка Δxi стремится к нулю, то есть
где a – нижний предел интегрирования; b – верхний предел интегрирования; f(x) – подынтегральная функция;
f(x)dx – подынтегральное выражение.

Слайд 3

Свойства определённого интеграла
Свойства определённого интеграла аналогичны свойствам неопределённого интеграла. Дополнительные свойства:
1.

, где ;
2. ;
3.
4. Пусть функция f(x) непрерывна на [a;b], тогда существует по крайней мере одна точка такая, что выполнено равенство .
Здесь f(c) называется средним значением функции.

3.2 Определённые интегралы
3.2.1 Основные понятия

Слайд 4

1. Использование формулы Ньютона-Лейбница.
Пусть f(x) непрерывна на отрезке [a;b] и

F(x) – одна из её первообразных, тогда справедлива формула
,
называемая формулой Ньютона-Лейбница.
Пример 1 Вычислить определённый интеграл .
Решение.
Ответ: 2.

3.2 Определённые интегралы
3.2.2 Способы вычисления определённого интеграла

Слайд 5

2. Использование замены переменной.
Необходимо вычислить интеграл , где f(x) –непрерывная

функция на [a;b]. Перейдем к новой переменной t, полагая x=φ(t). Пусть a=φ(α), b=φ(β), кроме того, при изменении t от α до β значения функции φ(t) не выходят за пределы отрезка [a;b]. Предположим, что функция φ(t) непрерывно дифференцируема на промежутке [a;b], то справедлива следующая формула замены переменной:

3.2 Определённые интегралы
3.2.2 Способы вычисления определённого интеграла

Слайд 6

3.2 Определённые интегралы
3.2.2 Способы вычисления определённого интеграла
Пример 2 Вычислить определённый интеграл

.
Решение.
Ответ: 5,25.

Слайд 7

Пусть на отрезке [a;b] задана неотрицательная непрерывная функция y=f(x). Фигура, ограниченная

сверху графиком y=f(x), снизу – осью Оx, сбоку прямыми x=a и y=b, называется криволинейной трапецией.
Геометрический смысл определённого интеграла:
, (1)
где S – площадь криволинейной трапеции.
Рис. 1

3.2 Определённые интегралы
3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат

Слайд 8

Если фигура, площадь которой необходимо вычислить, ограничена сверху графиком функции y=f(x),

снизу – графиком функции y=g(x), а сбоку прямыми x=a и x=b, то её площадь вычисляется по формуле:
(2)
Рис. 2