Содержание
- 2. Вывод формул общего решения ЛОУ 2-го порядка Корни характеристического уравнения Случай 1. Если , то характеристическое
- 3. Продолжение Случай 2. Если , то характеристическое уравнение имеет одинаковые корни . Частные решения ЛОУ выбираем
- 4. Продолжение Случай 3. Если , то характеристическое уравнение имеет два комплексно-сопряженных корня и , где и
- 5. Общее решение ЛОУ 2-го порядка в зависимости от корней характеристического уравнения 1. Если , то 2.
- 6. Пример Найти общее решение уравнения . Составим характеристическое уравнение . Его корни действительны и различны: .
- 7. Пример Решить уравнение y′′+4y′+4y =0. Характеристическое уравнение имеет два кратных корня , поэтому искомое общее решение
- 8. Пример Решить уравнение y′′+4y′+13y =0. Составим характеристическое уравнение . Корни этого уравнения комплексно-сопряженные. Общее решение исходного
- 9. Теорема о структуре общего решения линейного дифференциального уравнения 2-го порядка Общее решение уравнения y′′+py′+qy = f(x),
- 10. Подбор частного решения ЛНОУ по виду правой части методом неопределенных коэффициентов 1. Пусть . Тогда частное
- 11. Продолжение 2. Пусть , где -заданный многочлен . Тогда частное решение уравнения ищут в виде: а)если
- 12. В правой части уравнения-многочлен 1.Пусть , где -заданный многочлен. Это частный случай при =0. Тогда а)если
- 13. В правой части уравнения-тригонометрический полином 5. Пусть где степени многочленов и вообще говоря различны. Тогда а)если
- 14. Продолжение б)если , то частное решение ищут в виде: Пример: указать вид частного решения уравнения .
- 15. Решить уравнение . . Корни этого уравнения действительны и различны, поэтому общее решение соответствующего однородного уравнения
- 17. Скачать презентацию














 Доли и части от числа
Доли и части от числа Математическая логика
Математическая логика Теория графов: основные понятия и определения
Теория графов: основные понятия и определения Устный счет
Устный счет Нахождение части от числа и нахождение числа по его части
Нахождение части от числа и нахождение числа по его части Высказывания великих людей о математике
Высказывания великих людей о математике Прямоугольный треугольник. Решение задач
Прямоугольный треугольник. Решение задач Основы дисперсионного анализа. Однофакторный дисперсионный анализ
Основы дисперсионного анализа. Однофакторный дисперсионный анализ Абсолютные и относительные показатели
Абсолютные и относительные показатели Тригонометрия. Вычисление и преобразование выражений. Занятие – консультация (11 класс)
Тригонометрия. Вычисление и преобразование выражений. Занятие – консультация (11 класс) Тренажёр. Табличное умножение. В сказочном лесу
Тренажёр. Табличное умножение. В сказочном лесу Множества. Операции над множествами
Множества. Операции над множествами Числовые и буквенные выражения
Числовые и буквенные выражения Решение задач с помощью уравнений. 7 класс алгебра
Решение задач с помощью уравнений. 7 класс алгебра Ященко И.В. Приглашение на математический праздник
Ященко И.В. Приглашение на математический праздник Подсчёт вариантов с помощью графов. Агебра, 7 класс
Подсчёт вариантов с помощью графов. Агебра, 7 класс Степень с натуральным показателем
Степень с натуральным показателем Математика без границ. Конкурс
Математика без границ. Конкурс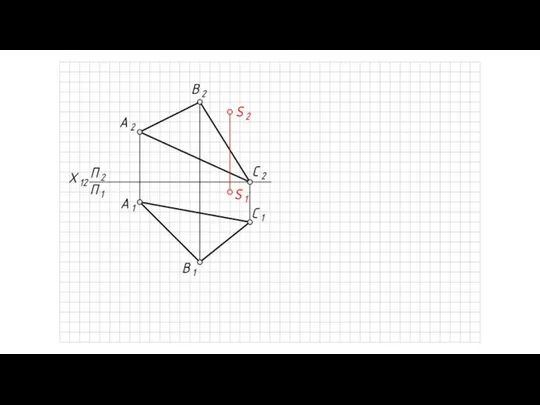 Замена расстояние от точки до плоскости
Замена расстояние от точки до плоскости Сложение и вычитание. Разминка
Сложение и вычитание. Разминка Популярные числа
Популярные числа Решение неравенств методом интервалов
Решение неравенств методом интервалов Модуль числа
Модуль числа МНОГОУГОЛЬНИКИ 5 класс
МНОГОУГОЛЬНИКИ 5 класс  Индивидуальные образовательные траектории в образовательной программе школы Опыт работы учителя математики МОУ «Цивильская С
Индивидуальные образовательные траектории в образовательной программе школы Опыт работы учителя математики МОУ «Цивильская С Путешествие в гости к Деду Морозу
Путешествие в гости к Деду Морозу Практические способы построения параллельных прямых
Практические способы построения параллельных прямых Способы решения квадратных уравнений
Способы решения квадратных уравнений