Линейные ДУ второго порядка

Где у – искомая функция, p(x), g(x), f(x) – функции, непрерывные

Если разрешить это уравнение относительно второй производной, то оно будет являться

ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДУ ВТОРОГО ПОРЯДКА

Линейным однородным ДУ второго
порядка называется уравнение вида

7

А

ТЕОРЕМА.

Пусть функции у1(х) и у2(х) – решения уравнения (7). Тогда функция

Доказательство:

Найдем первую и вторую производные от этой функции:

и подставим их в

(поскольку функции у1 (х) и у2 (х) – решения этого уравнения).

Ранее было введено понятие линейной зависимости векторов. По аналогии можно ввести

Линейно зависимые функции оказываются пропорциональными, т.е.

Обратное утверждение тоже верно: если

Введем для случая двух функций

определитель Вронского

ТЕОРЕМА.

Если функции у1 (х) и у2 (х) линейно зависимы
на интервале

Доказательство:

Пусть функции у1 (х) и у2 (х) линейно зависимы на интервале

Вторую часть теоремы докажем от противного: Пусть функции у1 (х) и

ТЕОРЕМА.

Пусть решения уравнения (7) у1(х) и у2(х) – линейно независимы на

Доказательство:

Функция

является решением уравнения (7). Нужно показать, что она представляет собой общее

Составим из них начальные условия:

Подставим в левую часть этих условий функцию

Определитель этой системы

есть определитель Вронского.
Поскольку у1 и у2 – линейно независимы,

Подставляем эти решения в исходную функцию:

Получили частное решение, удовлетворяющее произвольно выбранным

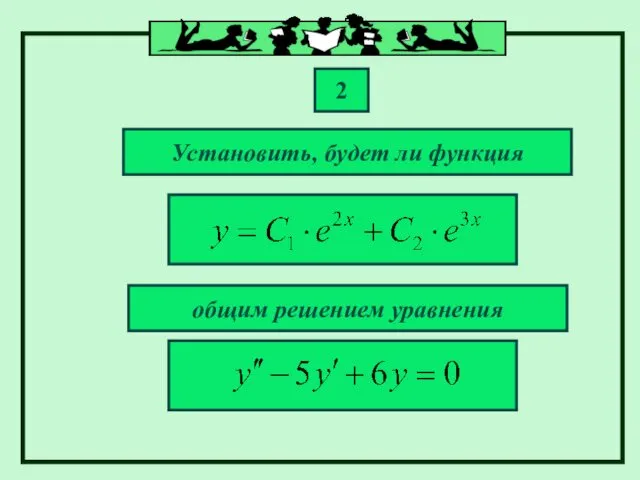
ПРИМЕРЫ.

Установить, будет ли функция

1

общим решением уравнения

Решение:

По теореме это решение будет общим, если функции

являются решением этого

Следовательно, данные функции являются решением этого уравнения. Проверим, будут ли они

Следовательно, данные функции являются линейно независимыми.
Таким образом, функция

будет общим решением заданного

Установить, будет ли функция

2

общим решением уравнения

Решение:

По теореме это решение будет общим, если функции

являются решением этого

Следовательно, данные функции являются решением этого уравнения. Проверим, будут ли они

Следовательно, данные функции являются линейно независимыми.
Таким образом, функция

будет общим решением заданного

ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДУ ВТОРОГО ПОРЯДКА

Линейным неоднородным ДУ второго
порядка называется уравнение вида

8

Б

ТЕОРЕМА.

Общее решение уравнения (8) состоит
из суммы его частного решения и общего
решения

Доказательство:

Пусть

- общее решение соответствующего однородного уравнения (7), и пусть

- какое-либо частное

Сначала покажем, что функция

является решением уравнения (8).

Подставляем в уравнение (8):

=

Учтем, что

Тогда

=

Таким образом, функция

является решением уравнения (8).
Теперь нужно показать, что она

Поскольку

Подставляем в это уравнение:

Следовательно, эту разность можно записать в виде частного решения однородного уравнения

Таким образом, любое решение уравнения (8) можно получить по формуле:

путем подбора

Таким образом, чтобы найти общее
решение неоднородного уравнения (8) нужно
найти

Для нахождения частного решения неоднородного уравнения используется

метод вариации постоянных

Пусть

- общее решение

Тогда

Дифференцируем это равенство:

Положим функции

такими, что выполняется равенство:

Тогда

Находим вторую производную:

Подставляем найденные производные в уравнение (8):

Перегруппируем слагаемые с С1(х) и С2(х)

Так как у1(х) и у2(х) – решения однородного уравнения (7), то

Объединим его с равенством

Получаем систему:

Определитель этой системы

есть определитель Вронского.
Поскольку у1(х) и у2(х) – линейно независимы,

Интегрируем эти выражения, получим

Подставляем их в выражение

и получаем частное решение

ПРИМЕР.

Найти общее решение уравнения

Решение:

Рассмотрим однородное уравнение:

Ранее было показано, что его общее решение

Следовательно, частное решение

Пусть

Тогда

Подставляем в уравнение:

Получаем:

Первое уравнение умножаем на 2 и вычтем его из второго:

Теперь

Интегрируем эти выражения:

При интегрировании можно опустить произвольные постоянные т.к. мы ищем любое частное