Содержание
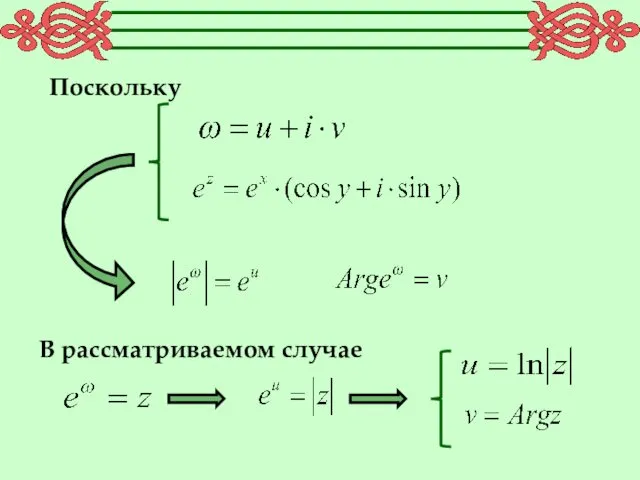
- 2. Поскольку В рассматриваемом случае
- 3. Где -число действительное и положительное. -известный из курса математики логарифм действительной величины.
- 4. Ввиду многозначности аргумента логарифм является многозначной функцией, действительная часть которого определяется однозначно, а мнимая содержит неопределенное
- 5. В полученной формуле главное значение логарифма будет при к=0. Если z=x – действительное число, то Поэтому
- 6. Будем обозначать главное значение логарифма
- 7. ПРИМЕРЫ. Вычислить 1 2 3 4 5 6
- 8. РЕШЕНИЕ. 1 2 3
- 9. 4 5
- 10. 6
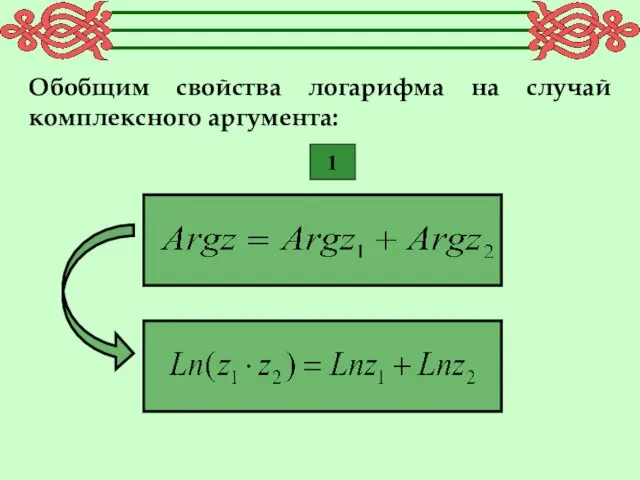
- 11. Обобщим свойства логарифма на случай комплексного аргумента: 1
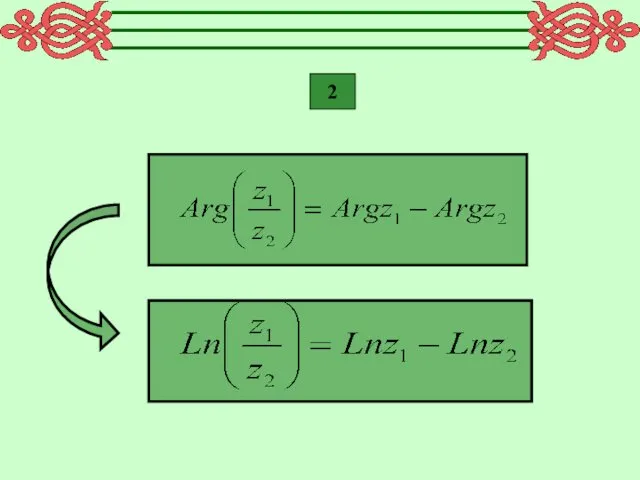
- 12. 2
- 13. 3
- 14. 4
- 15. По определению логарифмической функции для любого комплексного числа Тогда Поскольку логарифм – многозначная функция, то функция
- 16. ПРИМЕРЫ. Вычислить 1 2
- 17. РЕШЕНИЕ. 1 Главное значение 2
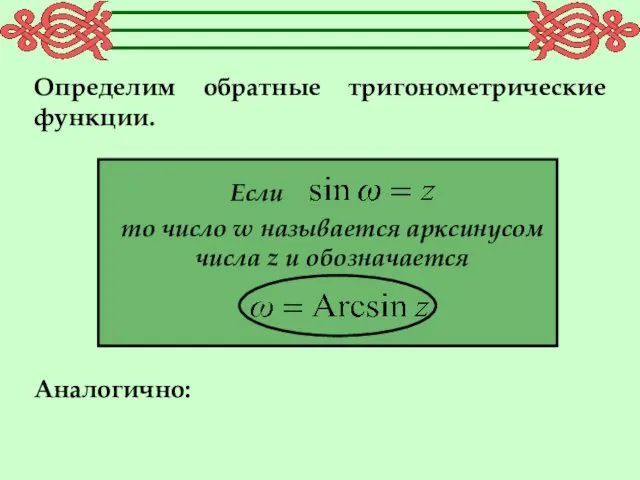
- 18. Определим обратные тригонометрические функции. Если то число w называется арксинусом числа z и обозначается Аналогично:
- 19. Если то число w называется арккосинусом числа z и обозначается Если то число w называется арктангенсом
- 20. Если то число w называется арккотангенсом числа z и обозначается
- 21. Если то Обозначим
- 22. Решаем это квадратное уравнение:
- 23. Т.к. логарифм многозначен, а корень – двухзначен, то арксинус тоже будет многозначной функцией. Если z –
- 24. Но поскольку то все значения логарифма числа, модуль которого равен 1, являются чисто мнимыми, а так
- 25. Если то
- 26. Если z – действительное число, то числа будут сопряженными с одинаковыми модулями.
- 27. Тогда все значения логарифма будут чисто мнимыми. Поскольку стоит множитель То значения арктангенса будут действительными. В
- 28. ПРИМЕРЫ. Вычислить 1 2
- 29. РЕШЕНИЕ. 1
- 31. Скачать презентацию






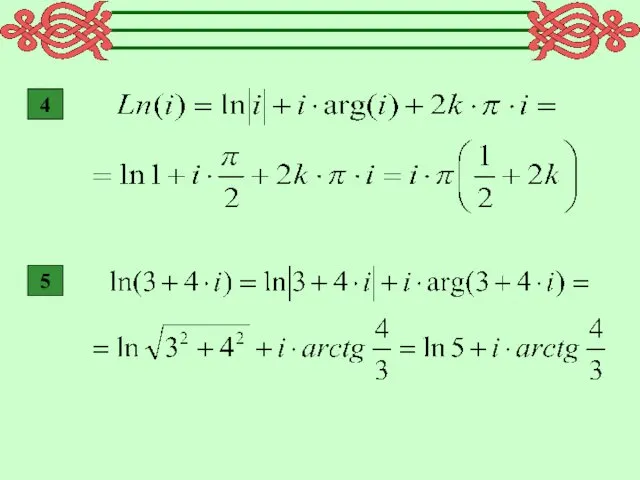

















 Презентация на тему Неопределенный интеграл
Презентация на тему Неопределенный интеграл Обыкновенные дроби. Действия с дробями
Обыкновенные дроби. Действия с дробями Перестановки
Перестановки Показательные уравнения
Показательные уравнения Нахождение угла между плоскостями различными методами
Нахождение угла между плоскостями различными методами Открытый банк заданий по математике Задача №14
Открытый банк заданий по математике Задача №14 Четырёхугольник
Четырёхугольник Непрерывные случайные величины
Непрерывные случайные величины Презентация на тему Изменения в природе
Презентация на тему Изменения в природе  Основы математического моделирования. Расчеты «из первых принципов»
Основы математического моделирования. Расчеты «из первых принципов» Арифметическая прогрессия. Тест
Арифметическая прогрессия. Тест Система координат в пространстве
Система координат в пространстве Презентация по математике "Столбчатые и линейные диаграммы" - скачать
Презентация по математике "Столбчатые и линейные диаграммы" - скачать  Математический тренажёр «Наряжаем ёлочку». Случаи сложения и вычитания вида 26+4, 30-7
Математический тренажёр «Наряжаем ёлочку». Случаи сложения и вычитания вида 26+4, 30-7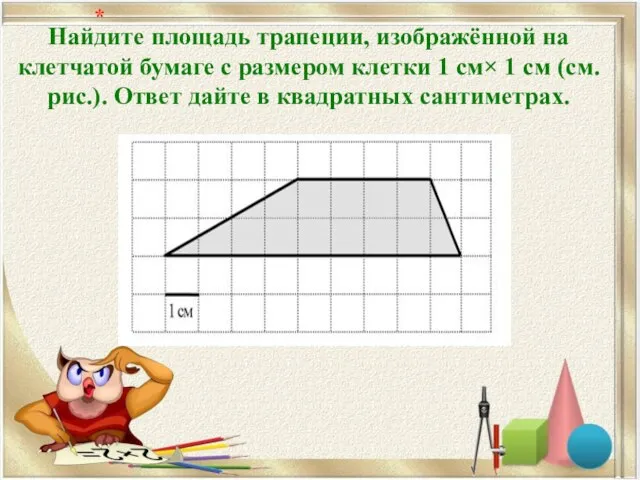 Решение задач на нахождение площади фигур
Решение задач на нахождение площади фигур Состав числа 7
Состав числа 7 Делители и кратные. 6 класс
Делители и кратные. 6 класс Свойства сложения
Свойства сложения Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Операции на нечетких множествах
Операции на нечетких множествах Умножение. Множители. Произведение
Умножение. Множители. Произведение Формулы тригонометрии
Формулы тригонометрии Урок-экскурсия в страну Отрицательных чисел
Урок-экскурсия в страну Отрицательных чисел Цифра и число 1
Цифра и число 1 Решение задач по механике с использованием тригонометрии Для профильного физико-математического 10 класса
Решение задач по механике с использованием тригонометрии Для профильного физико-математического 10 класса Презентация по математике "Перевод чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную" - ска
Презентация по математике "Перевод чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную" - ска Функции многих переменных
Функции многих переменных Количество вещества
Количество вещества