Содержание
- 2. Правила пользования презентацией Выход в содержание Возврат к предыдущему слайду Переход к следующему слайду Подчёркнутое слово
- 3. Содержание Предисловие Что такое логика? - История изучения - Высказывания Алгебра логики - Действия над высказываниями
- 4. Предисловие В повседневной жизни мы часто сталкиваемся с ситуациями, когда не знаем, как прийти к выводу
- 5. Предмет логики Логика (др.-греч. «λογική» — «искусство рассуждения») — наука, изучающая законы и формы мышления.
- 6. История Как самостоятельная наука логика оформилась в трудах греческого философа Аристотеля (384-322 г.г до н.э.). Он
- 7. Высказывания Высказывание – утвердительное предложение, относительно которого можно сказать истинно оно или ложно. Обычно высказывания обозначаются
- 8. Алгебра высказываний Дизъюнкция Импликация Эквиваленция Строгая дизъюнкция Конъюнкция Действия над высказываниями Отрицание
- 9. Приоритет выполнения операций Аν(В ~С) ∧ А → (ВνС) 1. Действия в скобках 1 1 2
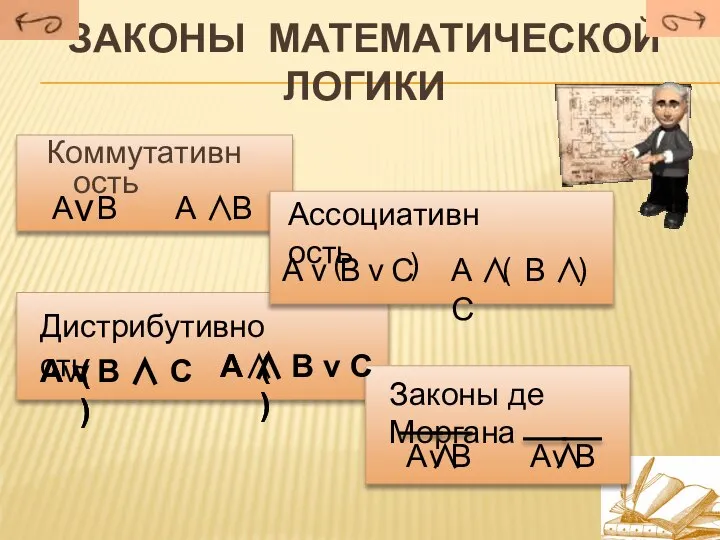
- 10. Законы математической логики Коммутативность А В ν Ассоциативность А ν В ν С ( ) А
- 11. Законы алгебры логики 1. А = А 2. А ν А = А 3. А ∧
- 12. Отрицание Отрицанием высказывания А называется такое высказывание, что В ложно, когда А истинно и В истинно,
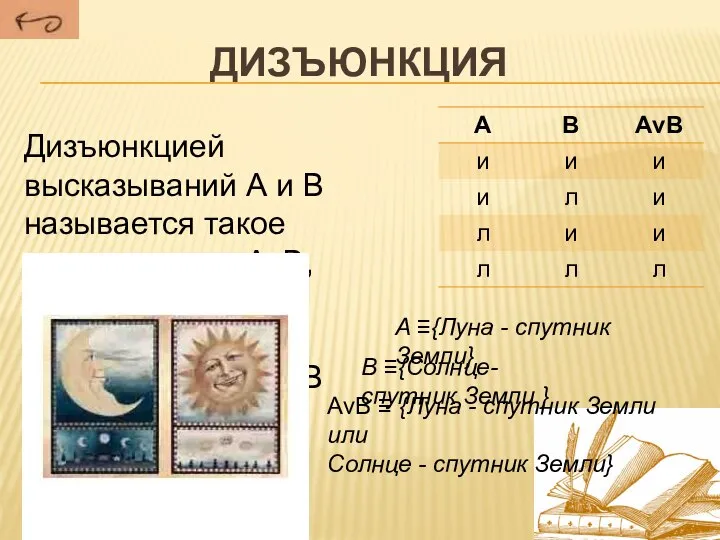
- 13. Дизъюнкция Дизъюнкцией высказываний А и В называется такое высказывание АνВ, ложное лишь в том случае, если
- 14. импликация Импликацией высказываний А и В называется такое высказывание А→В, ложное лишь в том случае, когда
- 15. конъюнкция Конъюнкцией высказываний А и В называется такое высказывание А∧В, истинное лишь в том случае, если
- 16. эквиваленция Эквиваленцией высказываний А и В называется такое высказывание А~В, истинное когда А и В –
- 17. Строгая дизъюнкция Строгой дизъюнкцией высказываний А и В называют высказывание А⊕В, истинное лишь в случаях, когда
- 18. Тогда, слушайте загадку! Да, капитан! Так точно, капитан! Я не слышу!! Согласно инструкции я должен находиться
- 19. Разгадали? Давайте проверим Пусть А≡{Капитан присутствует на судне}, В≡{С судна выгружают груз}, С≡{Рулевой присутствует на судне},
- 20. Предикаты Утверждение, зависящее от переменной, заданной на определенном множестве и обращающееся в верное высказывание при конкретном
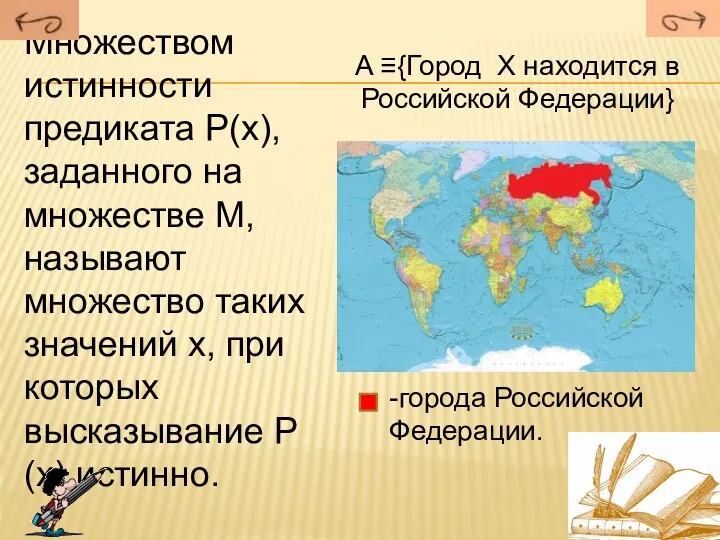
- 21. Множеством истинности предиката Р(х), заданного на множестве М, называют множество таких значений х, при которых высказывание
- 22. Для предикатов характерны те же действия, что и для высказываний, а именно: Конъюнкция Дизъюнкция Импликация Эквиваленция
- 23. Кванторы Одним из способов получения высказываний из предикатов является навешивание кванторов. Для этого перед предикатом пишут
- 24. квантор существования « ∃» Квантор существования — это символ, обозначающий единственное существование и читается как «существует»
- 25. квантор всеобщности «∀» Квантор всеобщности — это символ, обозначающий всеобщность и читается как «для любого» или
- 26. Заключение Таким образом, мы познакомились с основными понятиями алгебры логики, научились выполнять операции с высказываниями, определенными
- 27. Использованная литература Шабунин М.И. Математика. Алгебра. Начала анализа. http://ru.wikipedia.org
- 29. Скачать презентацию























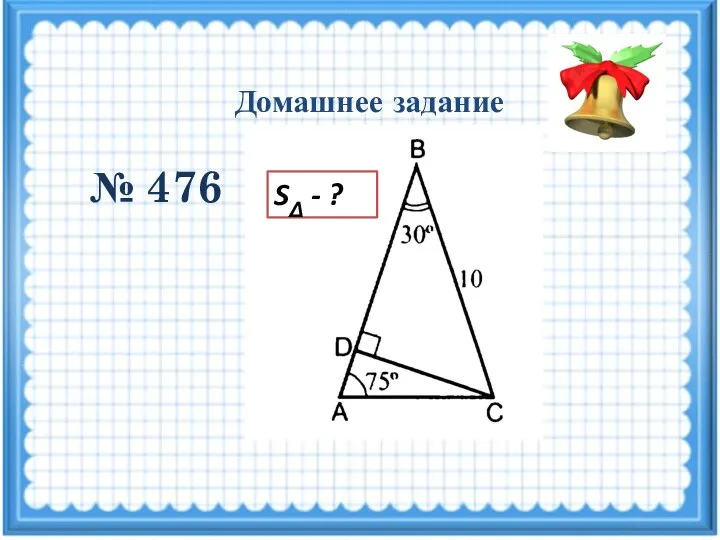 Домашнее задание № 476
Домашнее задание № 476 Математико-статистическое методы в педагогических исследованиях
Математико-статистическое методы в педагогических исследованиях Счастливый случай Урок – семинар “Функции и их графики” 9 класс
Счастливый случай Урок – семинар “Функции и их графики” 9 класс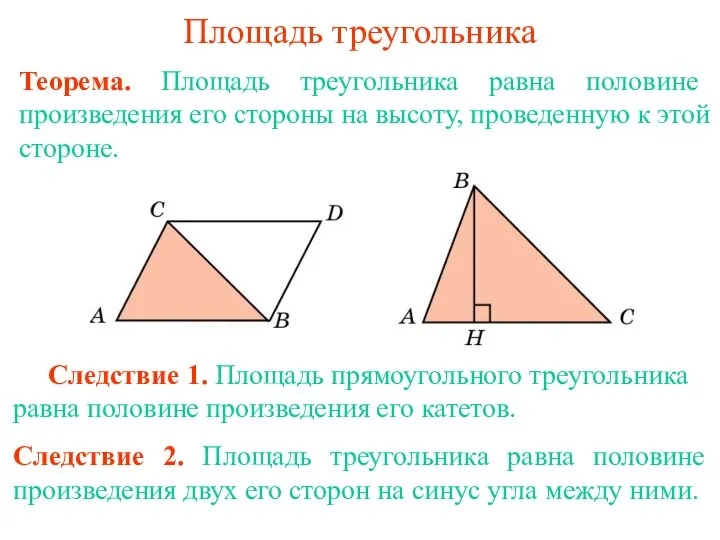 Площадь треугольника
Площадь треугольника Математическая викторина. 7 класс
Математическая викторина. 7 класс Взаимное расположение плоскостей. Параллельные плоскости
Взаимное расположение плоскостей. Параллельные плоскости Морской бой. Математическая игра
Морской бой. Математическая игра Столбчатые диаграммы
Столбчатые диаграммы Презентация по математике "Паралелльность прямых" - скачать бесплатно
Презентация по математике "Паралелльность прямых" - скачать бесплатно Преобразование иррациональных выражений
Преобразование иррациональных выражений Координатная плоскость. Рисуем координатами
Координатная плоскость. Рисуем координатами Методика изучения случайных величин и их характеристик в курсе алгебры и начала анализа
Методика изучения случайных величин и их характеристик в курсе алгебры и начала анализа Фабрика звезд. Игра
Фабрика звезд. Игра Дроби разные нужны, дроби разные важны! (6 класс)
Дроби разные нужны, дроби разные важны! (6 класс) Лист Мебиуса
Лист Мебиуса Урок математики
Урок математики Измерение углов
Измерение углов Предел последовательности
Предел последовательности Натуральные числа. Комбинаторные задачи
Натуральные числа. Комбинаторные задачи Обыкновенные дроби
Обыкновенные дроби Упрощение выражений (2)
Упрощение выражений (2) Многоугольники. Их формы
Многоугольники. Их формы Леонард Эйлер
Леонард Эйлер Тапкырлаучыны тамыр тамгасы тышына чыгару. Тапкырлаучыны тамыр тамгасы астына кертү. 8 klass
Тапкырлаучыны тамыр тамгасы тышына чыгару. Тапкырлаучыны тамыр тамгасы астына кертү. 8 klass Графики функций. Подготовка к ГИА
Графики функций. Подготовка к ГИА ПЛОЩАДЬ. ЕДИНИЦЫ ПЛОЩАДИ.
ПЛОЩАДЬ. ЕДИНИЦЫ ПЛОЩАДИ.  Положительные и отрицательные числа. 6 класс
Положительные и отрицательные числа. 6 класс Правила вычисления производных
Правила вычисления производных