Содержание
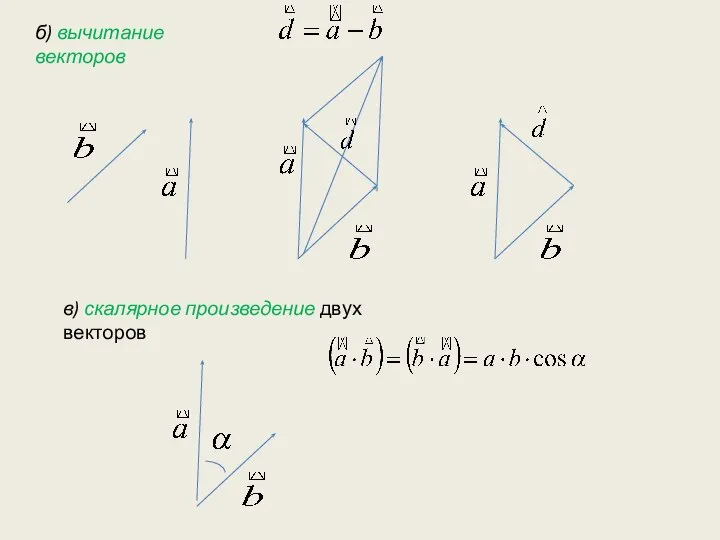
- 2. б) вычитание векторов в) скалярное произведение двух векторов
- 3. г) векторное произведение двух векторов д) произведение вектора на скаляр е) решение векторных треугольников сводится к
- 4. 2. Выражение вектора через его проекции на координатные оси. , ( или )- орты координатных осей
- 5. Координатная запись скалярного и векторного произведений: Смешанное произведение: Двойное векторное произведение: Можно запомнить так: «бас минус
- 6. 3. Предел. Если переменная величина (скорость, ускорение, сила) в рассматриваемом случае неограниченно приближается к какому –
- 7. Формулы дифференциального исчисления
- 8. Производная функции или вторая производная функции : Применение производных для исследования функций. В точках экстремума функции
- 9. Пример:
- 10. Для функции многих переменных ее полный дифференциал где - частные производные функции. Это производные по одному
- 11. 5. Интеграл. 5.1 Определенный интеграл Сумму при столь малых , что на каждом из этих интервалов
- 12. Основные свойства определенного интеграла.
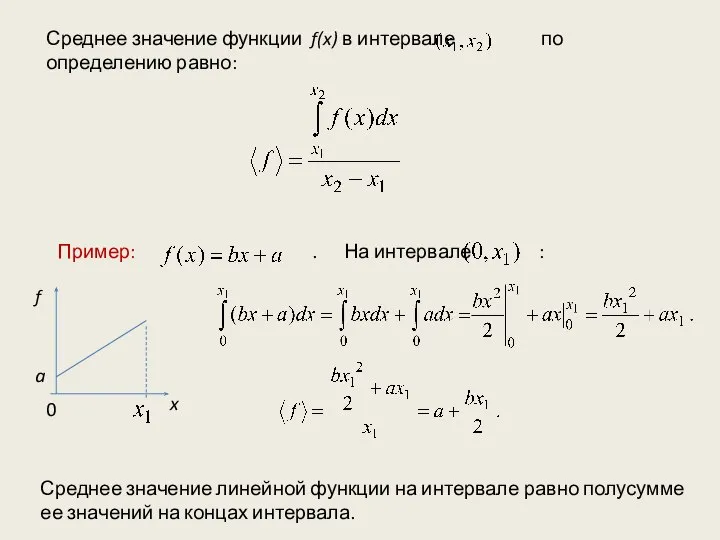
- 13. Среднее значение функции f(x) в интервале по определению равно: Пример: . На интервале : a f
- 14. 5.2 Неопределенный интеграл Если в задаче необходимо узнать не численный ответ: а саму зависимость , то
- 15. Формулы интегрального исчисления
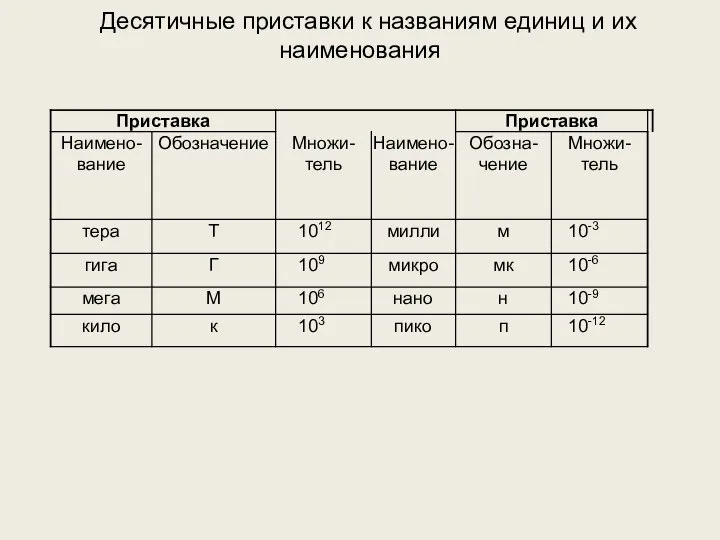
- 16. Десятичные приставки к названиям единиц и их наименования
- 17. Некоторые тригонометрические формулы
- 19. Скачать презентацию













 УРОК МАТЕМАТИКИ Тема «Решение задач на движение в противоположных направлениях»
УРОК МАТЕМАТИКИ Тема «Решение задач на движение в противоположных направлениях» Архитектура и параллелепипед
Архитектура и параллелепипед Оптимизация элементов треугольника при решении задачи «Как поспорили Иван Иванович с Иваном Никифоровичем»
Оптимизация элементов треугольника при решении задачи «Как поспорили Иван Иванович с Иваном Никифоровичем» Работу выполнила ученица 8 «А» класса МБОУ-Старокулаткинская СОШ №1 Рахматуллина Ляйсан Руководитель Умярова Р.А.- учитель мат
Работу выполнила ученица 8 «А» класса МБОУ-Старокулаткинская СОШ №1 Рахматуллина Ляйсан Руководитель Умярова Р.А.- учитель мат Как записывают и читают десятичные дроби
Как записывают и читают десятичные дроби Множество действительных чисел
Множество действительных чисел Квадратный корень из произведения и дроби
Квадратный корень из произведения и дроби Простейшие преобразования графиков функций
Простейшие преобразования графиков функций Уравнения
Уравнения Золотое сечение - Золотая пропорция
Золотое сечение - Золотая пропорция Поиграем! Вперёд за волшебным клубочком. 1класс
Поиграем! Вперёд за волшебным клубочком. 1класс Открытый урок математики в 3 классе в условиях развивающего обучения по программе « Начальная школа ХХI века» Учитель: Широков
Открытый урок математики в 3 классе в условиях развивающего обучения по программе « Начальная школа ХХI века» Учитель: Широков Преобразование выражений, содержащих радикалы
Преобразование выражений, содержащих радикалы Задачи экономического содержания на ЕГЭ по математике
Задачи экономического содержания на ЕГЭ по математике Урок математики. 3 класс Тема урока: Числитель и знаменатель дроби. Запись дробей.
Урок математики. 3 класс Тема урока: Числитель и знаменатель дроби. Запись дробей. Возведение степени в степень. Свойства действий со степенями
Возведение степени в степень. Свойства действий со степенями Равносильные уравнения и неравенства
Равносильные уравнения и неравенства Третий признак равенства треугольников
Третий признак равенства треугольников Площадь многоугольника
Площадь многоугольника Общие методы решения уравнений
Общие методы решения уравнений Логарифмы. Математический турнир
Логарифмы. Математический турнир Машинки от 0 до 10
Машинки от 0 до 10 Презентация по математике "Логарифмическая функция" - скачать
Презентация по математике "Логарифмическая функция" - скачать  Арифметические действия. Тест
Арифметические действия. Тест Организация выборочного наблюдения
Организация выборочного наблюдения Графический диктант (зрительный)
Графический диктант (зрительный) Модуль Геометрия часть II № 24-26
Модуль Геометрия часть II № 24-26 Интеллектуальная игра «Самый умный». Информатика. Математика
Интеллектуальная игра «Самый умный». Информатика. Математика