Содержание
- 2. М А Т Р И Ц Ы ОПРЕДЕЛЕНИЯ Матрицей размерности m x n называется прямоугольная таблица
- 3. М А Т Р И Ц Ы ОПРЕДЕЛЕНИЯ Матрицу обозначают: Матрица любой размерности называется нулевой (обозначают:
- 4. М А Т Р И Ц Ы Виды матриц Матрица размерности 1 x n называется матрицей-строкой:
- 5. М А Т Р И Ц Ы Виды матриц Квадратная матрица называется верхнетреугольной (нижнетреугольной), если все
- 6. М А Т Р И Ц Ы Виды матриц Квадратная матрица называется единичной (обозначают: Е), если
- 7. М А Т Р И Ц Ы Виды матриц Матрица, полученная из квадратной матрицы А заменой
- 8. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ Две матрицы одинаковой размерности называются равными,
- 9. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ Произведением матрицы А размерности m x
- 10. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ Примеры.
- 11. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ П р и м е ры.
- 12. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ Свойства линейных операций где матрицы одинаковой
- 13. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ 2) Умножение матриц Произведением матрицы размерности
- 14. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ Пример.
- 15. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ Пример. Следовательно, , т.е. умножение матриц
- 16. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ Свойства операции умножения матриц: (для квадратных
- 17. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ 3) Возведение в степень Эта операция
- 18. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ П р и м е ры.
- 19. М А Т Р И Ц Ы ОПЕРАЦИИ НАД МАТРИЦАМИ П р и м е ры.
- 20. М А Т Р И Ц Ы ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ О п р е д е л
- 21. М А Т Р И Ц Ы ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ 2) замена строки суммой этой строки и
- 22. М А Т Р И Ц Ы ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ 3) умножение строки на ненулевое число α,
- 23. М А Т Р И Ц Ы СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ О п р е д е
- 24. М А Т Р И Ц Ы СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ О п р е д е
- 25. М А Т Р И Ц Ы СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ Т е о р е м
- 26. М А Т Р И Ц Ы СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ О п р е д е
- 27. М А Т Р И Ц Ы РАНГ МАТРИЦЫ О п р е д е л
- 28. М А Т Р И Ц Ы СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ П р и м е р
- 29. М А Т Р И Ц Ы 3. СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ. П р и м е
- 30. М А Т Р И Ц Ы 3. СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ.
- 32. Скачать презентацию





























 Взаимное расположение прямой и плоскости
Взаимное расположение прямой и плоскости Полиномы над полями конечной характеристики
Полиномы над полями конечной характеристики Матрицы. Определения
Матрицы. Определения Булева алгебра
Булева алгебра Математика в изобразительном искусстве
Математика в изобразительном искусстве Презентация на тему Обозначение натуральных чисел. 5 класс.
Презентация на тему Обозначение натуральных чисел. 5 класс.  Преобразование Фурье
Преобразование Фурье Статистическое наблюдение. Тема 2
Статистическое наблюдение. Тема 2 Круговые диаграммы
Круговые диаграммы Умножение десятичных дробей
Умножение десятичных дробей Декартово произведение
Декартово произведение Признаки равенства треугольников
Признаки равенства треугольников Решение заданий С2
Решение заданий С2 Квадратичная функция и её график
Квадратичная функция и её график Числа Фибоначчи
Числа Фибоначчи Линейная функция. Построение графика функции у= 2х-1
Линейная функция. Построение графика функции у= 2х-1 Типы задач на дроби
Типы задач на дроби Исследование качества школьного математического и естественнонаучного образования TIMSS
Исследование качества школьного математического и естественнонаучного образования TIMSS Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Кластеризация значений пикселей изображений с учетом метрики цветового различия CIEDE-2000
Кластеризация значений пикселей изображений с учетом метрики цветового различия CIEDE-2000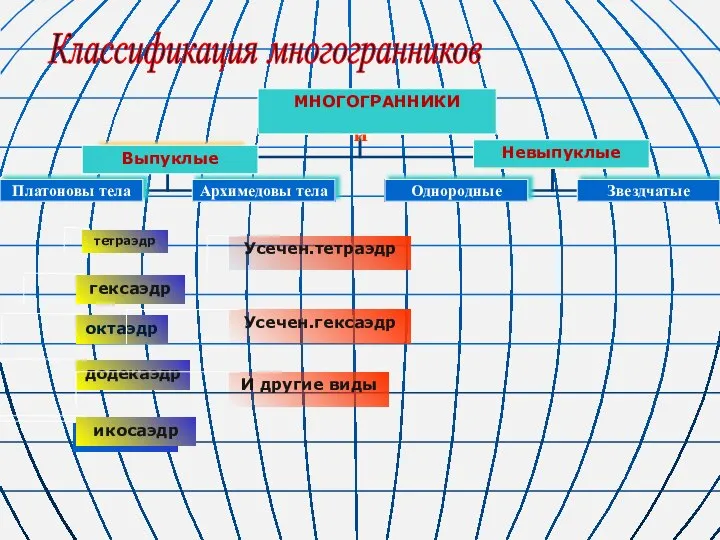 Классификация многогранников
Классификация многогранников Способ подстановки
Способ подстановки 20180306_prezentatsiya
20180306_prezentatsiya Что такое алгебра?
Что такое алгебра? Уравнения прямой и окружности
Уравнения прямой и окружности Длина окружности. Площадь круга
Длина окружности. Площадь круга Правильные многогранники
Правильные многогранники Решение уравнений tgx=a. Понятие арктангенса числа
Решение уравнений tgx=a. Понятие арктангенса числа