Содержание
- 2. Question 0. A continuous function f is defined on the interval [−1,1], and f 2(x) =
- 3. Question 0+. A function f is defined on the interval [−1,1], and f 2(x) = x
- 4. Mathematical Induction Let Sn, n = 1,2,3,… be statements involving positive integer numbers n. Suppose that
- 5. Question 1. Using the Principle of Mathematical Induction show that Solution. Step 1. The formula is
- 6. Now, the principle of mathematical induction tells us that our formula is correct for any n.
- 7. Answers to Questions from Light #3: Functions and Limits Question 2: Question 4: Question 3: Question
- 8. Calculus++ Also known as Hysterical Calculus
- 9. Question 1b. Using the Principle of Mathematical Induction show that Solution. Step 1. The formula is
- 10. Now, the principle of mathematical induction tells us that our formula is correct for any n.
- 11. Question 3a. Calculate the following sum Solution. We have
- 12. Question 5. Using the formula for the derivative of inverse function derive explicit formulae for the
- 13. Similar calculations yield the following formula for the derivative of arccot x. Hence
- 14. Question 6. Use the Cauchy criterion to show converges. Solution: It is sufficient to show that
- 15. Thus we set Therefore Thus, the sequence xn is fundamental, and therefore it converges to some
- 16. Picture of the Week All ICEF students are of the same height
- 17. Question 4. Let f (x) be a differentiable function such that the derivative is a continuous
- 18. b) Is it possible that there exists a number a such that Solution: The Mean Value
- 19. c) Let x1 be a solution of the equation f (x) = x. Find Solution: If
- 21. Скачать презентацию

![Question 0+. A function f is defined on the interval [−1,1],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/628607/slide-2.jpg)
















 Математическая симметрия
Математическая симметрия Решение задач на применение признаков равенства треугольников. 7 класс
Решение задач на применение признаков равенства треугольников. 7 класс Презентация на тему Прямоугольный параллелепипед. Куб.
Презентация на тему Прямоугольный параллелепипед. Куб.  Плоска система збіжних сил
Плоска система збіжних сил Презентация по математике "Угол. Прямой угол" - скачать бесплатно
Презентация по математике "Угол. Прямой угол" - скачать бесплатно Презентация на тему Преобразование целого выражения в многочлен
Презентация на тему Преобразование целого выражения в многочлен Сравнение фигур с помощью наложения
Сравнение фигур с помощью наложения Математическое моделирование в инвестиционном проектировании
Математическое моделирование в инвестиционном проектировании Расстояние от точки до фигуры
Расстояние от точки до фигуры Решение логарифмических уравнений
Решение логарифмических уравнений Решение логических задач
Решение логических задач Решение логарифмических неравенств, содержащих переменную в основании логарифма: методы, приемы, равносильные переходы
Решение логарифмических неравенств, содержащих переменную в основании логарифма: методы, приемы, равносильные переходы Конкретный смысл действия деления. Математика класс Моро М. И.
Конкретный смысл действия деления. Математика класс Моро М. И.  Четность и нечетность функции
Четность и нечетность функции Решение уравнения. (Задание 13)
Решение уравнения. (Задание 13) Аналитические функции
Аналитические функции Решение задач по теме Теорема о трёх перпендикулярах. 10 класс
Решение задач по теме Теорема о трёх перпендикулярах. 10 класс Вычитание двузначного числа из круглого
Вычитание двузначного числа из круглого Решение текстовых задач. Задание В13, ЕГЭ
Решение текстовых задач. Задание В13, ЕГЭ Задачи на готовых чертежах (Теорема Пифагора)
Задачи на готовых чертежах (Теорема Пифагора)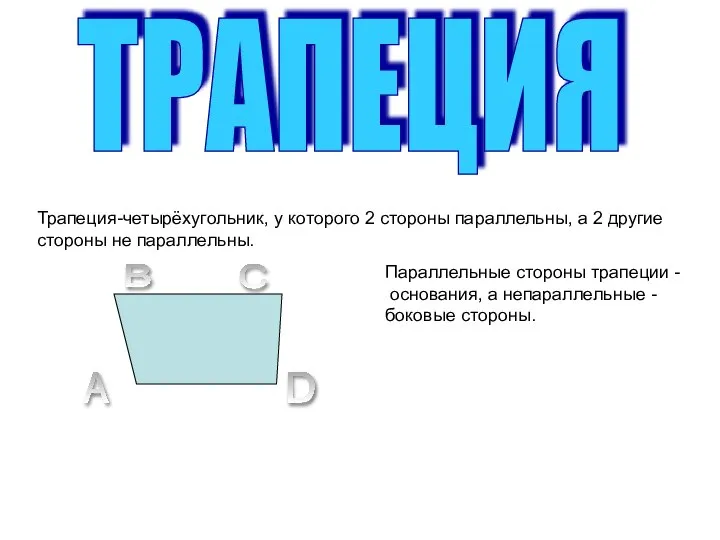 Трапеция
Трапеция Порівняння виразу і числа. Складання задач за поданою схемою розв’язання
Порівняння виразу і числа. Складання задач за поданою схемою розв’язання Площадь эллипса и окружности
Площадь эллипса и окружности Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Правила вычисления производных
Правила вычисления производных Последовательности: основные понятия и определения
Последовательности: основные понятия и определения Приведение дробей к общему знаменателю (урок в 6 классе) Лебедева Александра Львовна Учитель математики МОУ – Алферовская СОШ
Приведение дробей к общему знаменателю (урок в 6 классе) Лебедева Александра Львовна Учитель математики МОУ – Алферовская СОШ Функция, её свойства и график
Функция, её свойства и график