Содержание
- 2. Минор и алгебраическое дополнение элемента квадратной матрицы Опр. 14. Минором Мij элемента a ij квадратной матрицы
- 3. Вычисление определителя квадратной матрицы разложением по строке (столбцу) Теорема Лапласа 1. Определитель квадратной матрицы равен сумме
- 4. Вычисление определителя квадратной матрицы разложением по строке (столбцу) Теорема Лапласа 2. Сумма произведений элементов любой строки
- 5. Вычисление определителей Определитель удобно вычислять по строке или столбцу, содержащему наибольшее число нулей. Определитель диагональной и
- 6. Свойства определителей Можно доказать, используя теорему Лапласа 1. При транспонировании матрицы ее определитель не меняется. Свойства
- 7. Элементарные преобразования матриц
- 8. Обратная матрица Число а-1 называется обратным к числу а, отличному от 0, если а-1· а =
- 9. Вычисление обратной матрицы Необходимым и достаточным условием существования для А обратной матрицы является ее невырожденность. где
- 10. Ранг матрицы Опр. 18. Минором порядка k матрицы А размера называется определитель матрицы, полученной из А
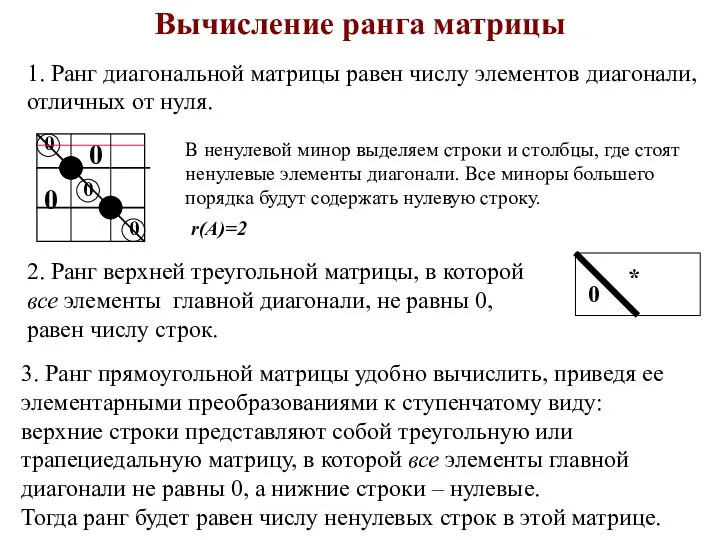
- 11. Вычисление ранга матрицы 1. Ранг диагональной матрицы равен числу элементов диагонали, отличных от нуля. 2. Ранг
- 13. Скачать презентацию









 Геометрический съезд (5 - 9 классы)
Геометрический съезд (5 - 9 классы) Смежные углы
Смежные углы Теория теней. Способ лучевых сечений. (Лекция 14)
Теория теней. Способ лучевых сечений. (Лекция 14) Квадратный трехчлен и его корни
Квадратный трехчлен и его корни Вычисления с многозначными числами
Вычисления с многозначными числами Задачи на дроби
Задачи на дроби Преобразование графиков функций
Преобразование графиков функций Использование метода ветвей и границ для поиска глобально оптимальных решений многокритериальных задач
Использование метода ветвей и границ для поиска глобально оптимальных решений многокритериальных задач Обработка результатов измерения. Диаграмма. 6 класс
Обработка результатов измерения. Диаграмма. 6 класс Космическое путешествие. Математика 6 класс
Космическое путешествие. Математика 6 класс Проценты. Основные задачи на проценты. Пособие для самостоятельного обучения учащихся 5-6 классов
Проценты. Основные задачи на проценты. Пособие для самостоятельного обучения учащихся 5-6 классов Презентация____
Презентация____ Прямоугольник
Прямоугольник Кратные и двойные интегралы
Кратные и двойные интегралы Древние меры длин
Древние меры длин Случайные величины и функции распределения (лекция 1)
Случайные величины и функции распределения (лекция 1) Модуль числа (часть 1)
Модуль числа (часть 1) Правильные многогранники
Правильные многогранники Правильные многоугольники
Правильные многоугольники Презентация по математике "Доли 4 класс" - скачать бесплатно
Презентация по математике "Доли 4 класс" - скачать бесплатно Устный счёт. (4 класс)
Устный счёт. (4 класс) Учебно-исследовательская работа «Счастливый случай или точный расчёт»
Учебно-исследовательская работа «Счастливый случай или точный расчёт» Задачи (устно)
Задачи (устно) Компьютерный практикум по алгебре в среде Matlab. Практическое занятие 2
Компьютерный практикум по алгебре в среде Matlab. Практическое занятие 2 Метод координат
Метод координат Повтарение по математике. Уравнение
Повтарение по математике. Уравнение Множества. Алгебра логики
Множества. Алгебра логики Дұрыс және бүрыс бөлшектер
Дұрыс және бүрыс бөлшектер