Содержание
- 2. Понятие конечных разностей Пусть задана функция y=f(x) на отрезке [x0,xn], который разбит на n одинаковых отрезков
- 3. Понятие конечных разностей Конечные разности первого порядка Δy0 = y1 – y0 Δy1 = y2 –
- 4. Понятие конечных разностей Конечные разности функций удобно располагать в таблицах, которые могут быть: Диагональными; Горизонтальными.
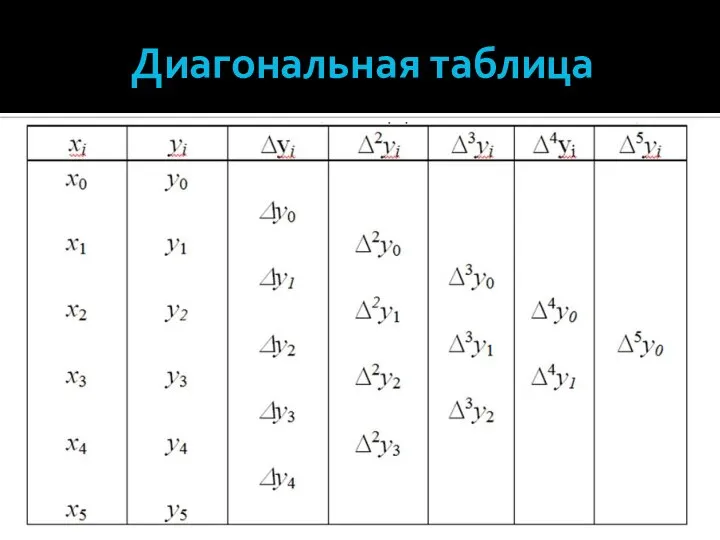
- 5. Диагональная таблица
- 6. Горизонтальная таблица
- 7. Первая интерполяционная формула Ньютона Пусть для функции y = f(x) заданы значения yi = f(xi) для
- 8. Задача построения многочлена сводится к определению коэффициентов аi из условий: Pn(x0)=y0 Pn(x1)=y1 . . . .
- 9. Определение коэффициентов Полагаем в интерполирующий полиноме x = x0 , тогда, т.к. второе, третье и другие
- 10. Определение коэффициентов Для определения а2 составим конечную разность второго порядка. При x = x2 получим:
- 11. Построение многочлена Аналогично можно найти другие коэффициенты. Общая формула имеет вид. Подставляя эти выражения в формулу
- 12. Первая интерполяционная формула Ньютона Этот многочлен называют интерполяционным полиномом Ньютона для интерполяции в начале таблицы (интерполирование
- 13. Первая интерполяционная формула Ньютона Для практического использования этот полином записывают в преобразованном виде, вводя обозначение t=(x
- 14. Пример Дана таблица значений теплоёмкости вещества в зависимости от температуры Cр =f(T). Определить значение теплоёмкости в
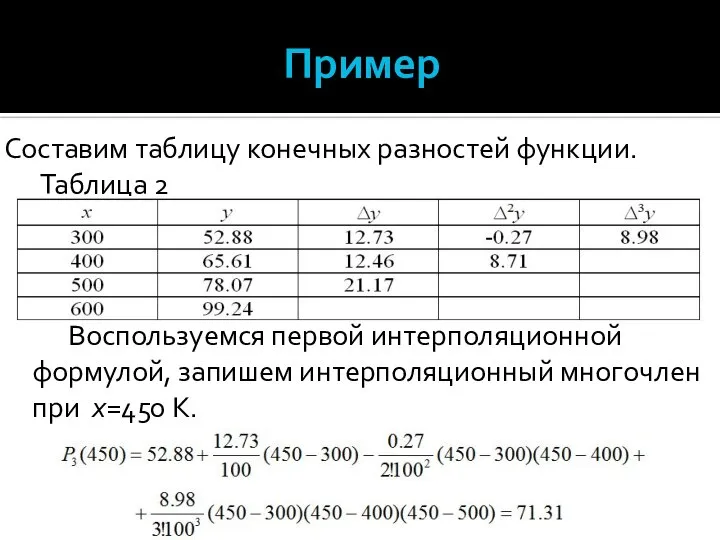
- 15. Пример Составим таблицу конечных разностей функции. Таблица 2 Воспользуемся первой интерполяционной формулой, запишем интерполяционный многочлен при
- 16. Пример Таким образом, теплоемкость при температуре 450 К будет: Сp(450)=71,31Дж/(моль ⋅ К) . Значение теплоемкости при
- 17. Вторая интерполяционная формула Ньютона
- 18. Область применения Второй интерполяционный полином Ньютона применяется для нахождения значений функций в точках, расположенных в конце
- 19. Определение коэффициентов Коэффициенты а0,а1,..., аn определяем из условия: Pn (xi ) = yi i=0,...,n. 1.Полагаем в
- 20. Определение коэффициентов 2.Полагаем x=xn-1, тогда: Pn(xn-1)=yn-1=yn+a1(xn-1 – xn) , h=xn – xn-1 , Следовательно: 3.Полагаем x=xn-2
- 21. Определение коэффициентов Аналогично можно найти другие коэффициенты многочлена:
- 22. Вторая интерполяционная формула Ньютона Подставляя эти выражения в формулу (1), получим вторую интерполяционную формулу Ньютона или
- 23. Вторая интерполяционная формула Ньютона Введем обозначения:
- 24. Вторая интерполяционная формула Ньютона Произведя замену , получим Это вторая формула Ньютона для интерполирования «назад».
- 25. Пример Вычислить теплоемкость (табл.1) для температуры Т=550 К. Воспользуемся второй формулой Ньютона и соответствующими конечными разностями
- 26. Пример Следовательно, значение теплоемкости при температуре 550 К равно: Ср(550)=97,01 Дж/(моль К).
- 27. Аппроксимация функций
- 28. Особенностью интерполяции являлось то, что интерполирующая функция строго проходит через узловые точки таблицы, т. е. рассчитанные
- 29. Особенности аппроксимации если для описания табличных данных будет выбрана функция с меньшим количеством коэффициентов (m
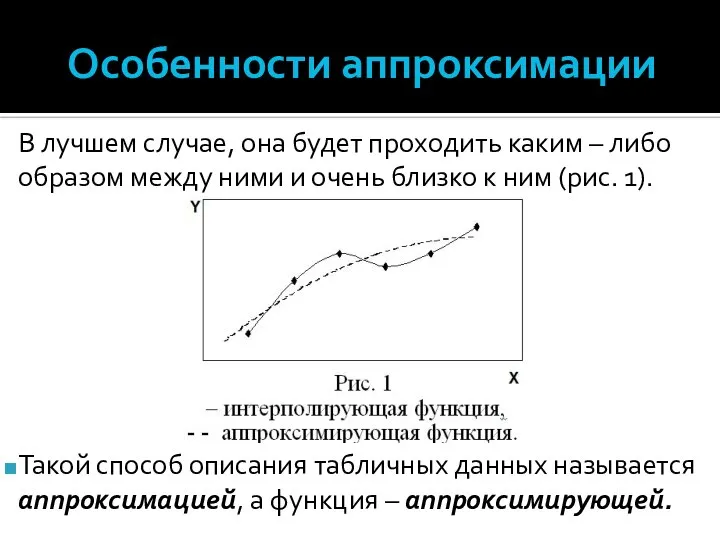
- 30. Особенности аппроксимации В лучшем случае, она будет проходить каким – либо образом между ними и очень
- 31. Условия применения аппроксимации Когда количество табличных значений очень велико. В этом случае интерполирующая функция будет очень
- 32. Условия применения аппроксимации Когда вид функции заранее определен. Такая ситуация возникает, если требуется описать экспериментальные точки
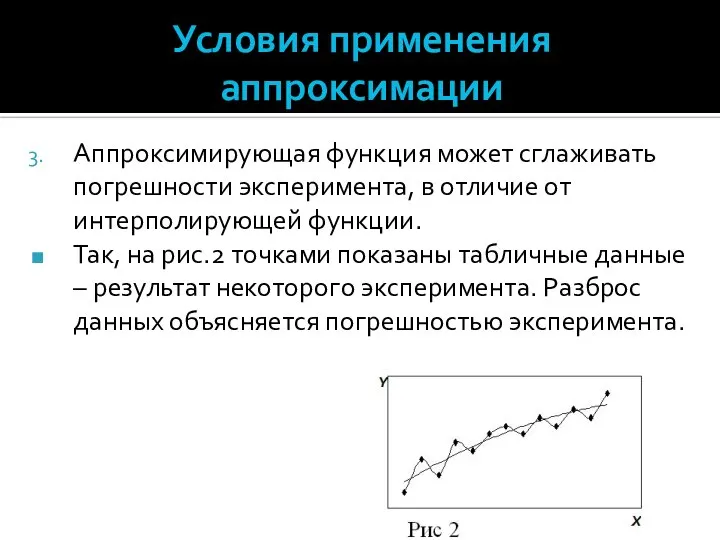
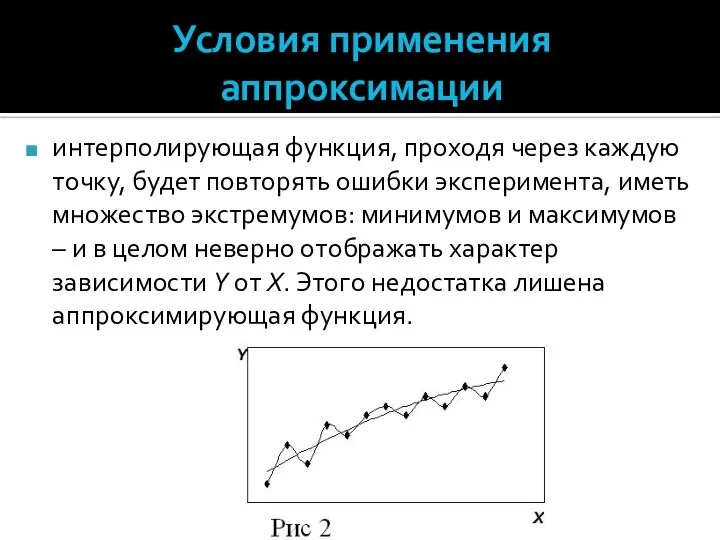
- 33. Условия применения аппроксимации Аппроксимирующая функция может сглаживать погрешности эксперимента, в отличие от интерполирующей функции. Так, на
- 34. Условия применения аппроксимации интерполирующая функция, проходя через каждую точку, будет повторять ошибки эксперимента, иметь множество экстремумов:
- 36. Скачать презентацию
![Понятие конечных разностей Пусть задана функция y=f(x) на отрезке [x0,xn], который](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1464914/slide-1.jpg)



























 Интегрирование. Определенный интеграл
Интегрирование. Определенный интеграл Векторное исчисление
Векторное исчисление Презентация по математике "Математическое образование в петровскую эпоху" - скачать
Презентация по математике "Математическое образование в петровскую эпоху" - скачать  Числовые выражения. Выражения с переменной. Уравнения. Математическая модель
Числовые выражения. Выражения с переменной. Уравнения. Математическая модель Умножение. Множители. Произведение
Умножение. Множители. Произведение Действия с одночленами
Действия с одночленами Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Сравнение десятичных дробей.
Сравнение десятичных дробей. Поле чудес. Геометрия 9 класс
Поле чудес. Геометрия 9 класс Математическое описание линейных САУ. Дифференциальные уравнения, передаточная функция. Временные и частотные характеристики
Математическое описание линейных САУ. Дифференциальные уравнения, передаточная функция. Временные и частотные характеристики Прямоугольные треугольники. Задания для устного счета
Прямоугольные треугольники. Задания для устного счета Площадь треугольника и медиана
Площадь треугольника и медиана Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Решение задач с помощью рациональных уравнений. 8 класс
Решение задач с помощью рациональных уравнений. 8 класс Умножение рациональных чисел
Умножение рациональных чисел Иррациональные числа
Иррациональные числа Бином Ньютона и треугольник Паскаля
Бином Ньютона и треугольник Паскаля Появление дробей. 5 класс
Появление дробей. 5 класс Умножение дробей на натуральное число
Умножение дробей на натуральное число Некоторые свойства касательной к окружности
Некоторые свойства касательной к окружности Презентация по математике "Сложение и вычитание чисел в пределах 20" - скачать бесплатно
Презентация по математике "Сложение и вычитание чисел в пределах 20" - скачать бесплатно Умножение десятичных дробей
Умножение десятичных дробей Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Подготовка к ЕГЭ по математике. Задания, 11 класс
Подготовка к ЕГЭ по математике. Задания, 11 класс Второй признак равенства треугольников
Второй признак равенства треугольников Extracurricular study in mathematics, 7th grade
Extracurricular study in mathematics, 7th grade Степень числа. 5 класс
Степень числа. 5 класс Диаграммы. Виды диаграмм
Диаграммы. Виды диаграмм