Содержание
- 2. Задачи Рассмотреть основные положения теории координат в пространстве . Рассмотреть наиболее выгодное расположение ПСК для основных
- 3. Создателем метода координат считают французского философа и математика Рене Декарта (1596-1650), который в последней части большого
- 4. Метод координат — весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами
- 5. Координатный метод решения задач
- 6. Алгоритм применения метода координат к решению координатных задач Выбираем в пространстве систему координат из соображений удобства
- 7. Координаты многогранников
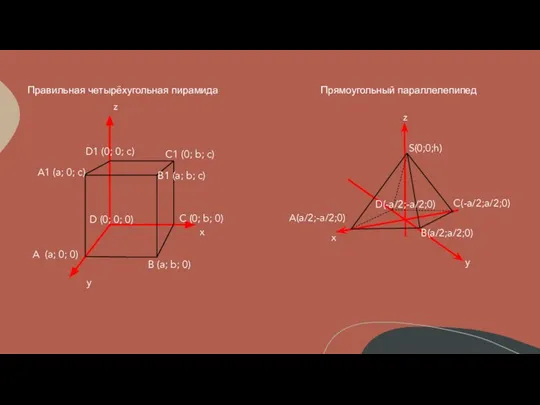
- 8. Прямоугольный параллелепипед Правильная четырёхугольная пирамида x y z C1 (0; b; c) D1 (0; 0; c)
- 9. Основные виды задач. Нахождение расстояния: Между прямой и плоскостью Между скрещивающимися прямыми Между двумя точками От
- 10. Расстояние между двумя точками Расстояние между точками А и В можно вычислить: 1) как длину отрезка
- 11. A Расстояние между скрещивающимися прямыми 1) равно расстоянию от любой точки одной из этих прямых до
- 12. Расстояние от точки до прямой можно вычислить: 1) как длину отрезка перпендикуляра, если удается включить этот
- 13. Расстояние от точки до плоскости 1) Равно расстоянию до плоскости α от произвольной точки Р, лежащей
- 14. Нахождение угла между прямыми. Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и
- 15. Нахождение угла между прямой и плоскостью Углом между плоскостью и не перпендикулярной ей прямой называется угол
- 16. Угол между плоскостями Угол между пересекающимися плоскостями можно вычислить: 1) как угол между прямыми, лежащими в
- 17. В правильной треугольной пирамиде SABC с вершиной S на сторонах AB и AC выбраны точки M
- 18. В кубе точки E, F, M – середины ребер AA 1 , AB 1 , CC
- 19. Используемая литература. Атанасян Л.С.и др. Геометрия, 10-11: учеб. для общеобразоват. учреждений: базовый и профил. уровни.- 17
- 20. Вывод: Существует ряд стереометрических задач, для которых более рациональным методом решения является не поэтапно-вычислительный, а координатный.
- 21. Спасибо за внимание.
- 23. Скачать презентацию



















 Презентация по математике "Сумма и разность десятичных дробей" - скачать бесплатно
Презентация по математике "Сумма и разность десятичных дробей" - скачать бесплатно Производная степенной функции УРОК алгебры и начала анализа в 11 «Б» классе учителя лицея № 179 ПАК НАТАЛЬИ НИКОЛАЕВНЫ
Производная степенной функции УРОК алгебры и начала анализа в 11 «Б» классе учителя лицея № 179 ПАК НАТАЛЬИ НИКОЛАЕВНЫ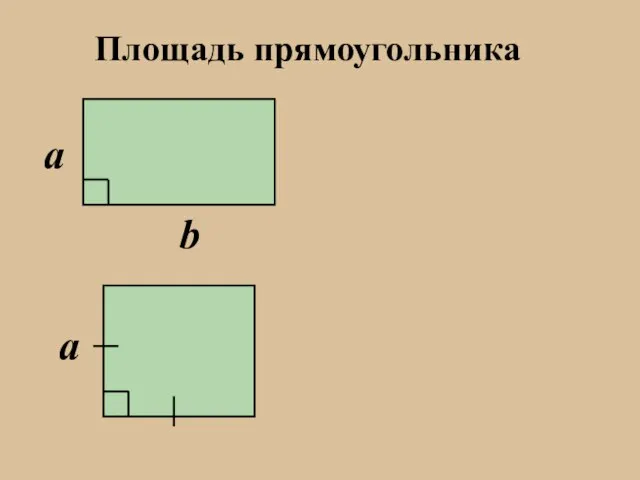 Площади геометрических фигур. Задачи
Площади геометрических фигур. Задачи Преобразование временных рядов в последовательности гистограмм как метод получения космофизической информации
Преобразование временных рядов в последовательности гистограмм как метод получения космофизической информации Introduction to vectors
Introduction to vectors Проверка математических данных в произведении Н. Носова «Незнайка на Луне»
Проверка математических данных в произведении Н. Носова «Незнайка на Луне» Григорий Яковлевич Перельман
Григорий Яковлевич Перельман Простые задачи
Простые задачи Презентация по математике "Единицы площади урок" - скачать
Презентация по математике "Единицы площади урок" - скачать  Математические модели. Типы. Требования к математическим моделям
Математические модели. Типы. Требования к математическим моделям Презентация по математике "Математическая разминка" - скачать бесплатно
Презентация по математике "Математическая разминка" - скачать бесплатно Параллелепипед построение
Параллелепипед построение Мышь. Примеры
Мышь. Примеры Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Устный счёт
Устный счёт Вписанная и описанная окружности
Вписанная и описанная окружности Размещения без повторений. Комбинации в задачах
Размещения без повторений. Комбинации в задачах Погрешности измерений
Погрешности измерений Нелинейное программирование
Нелинейное программирование Перестановка слагаемых. Применение переместительного свойства
Перестановка слагаемых. Применение переместительного свойства Математические модели сейсмоизолирующих устройств
Математические модели сейсмоизолирующих устройств Тригонометрические тождества. Преобразование тригонометрических выражений
Тригонометрические тождества. Преобразование тригонометрических выражений Спецглавы высшей математики. Лекционный материал
Спецглавы высшей математики. Лекционный материал Презентация по математике "ТРЕНАЖЕРЫ ПО МАТЕМАТИКЕ ДЛЯ ПОДГОТОВКИ К ЕГЭ 2015" - скачать бесплатно
Презентация по математике "ТРЕНАЖЕРЫ ПО МАТЕМАТИКЕ ДЛЯ ПОДГОТОВКИ К ЕГЭ 2015" - скачать бесплатно Вероятность равновозможных событий
Вероятность равновозможных событий Уроки математики в 6 классе по теме: «Симметрия»
Уроки математики в 6 классе по теме: «Симметрия» 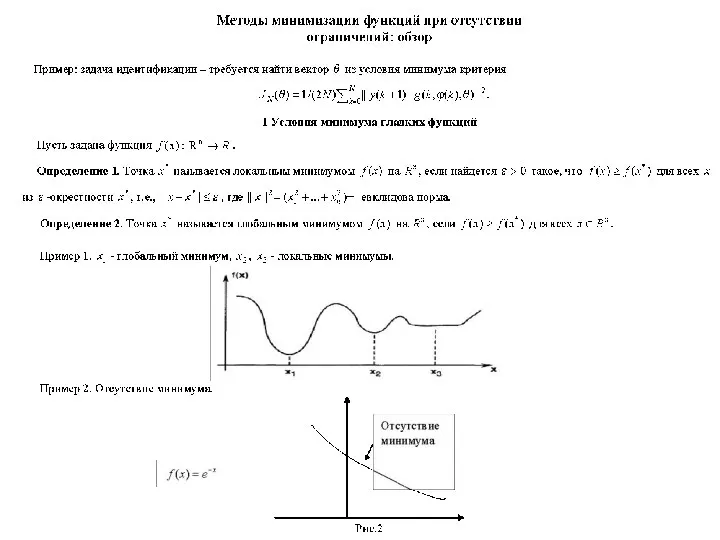 Методы минимизации функций при отсутствии ограничений: обзор
Методы минимизации функций при отсутствии ограничений: обзор Теорія ймовірності. (11 клас)
Теорія ймовірності. (11 клас)